[ABC324F] Beautiful Path - 洛谷

思路

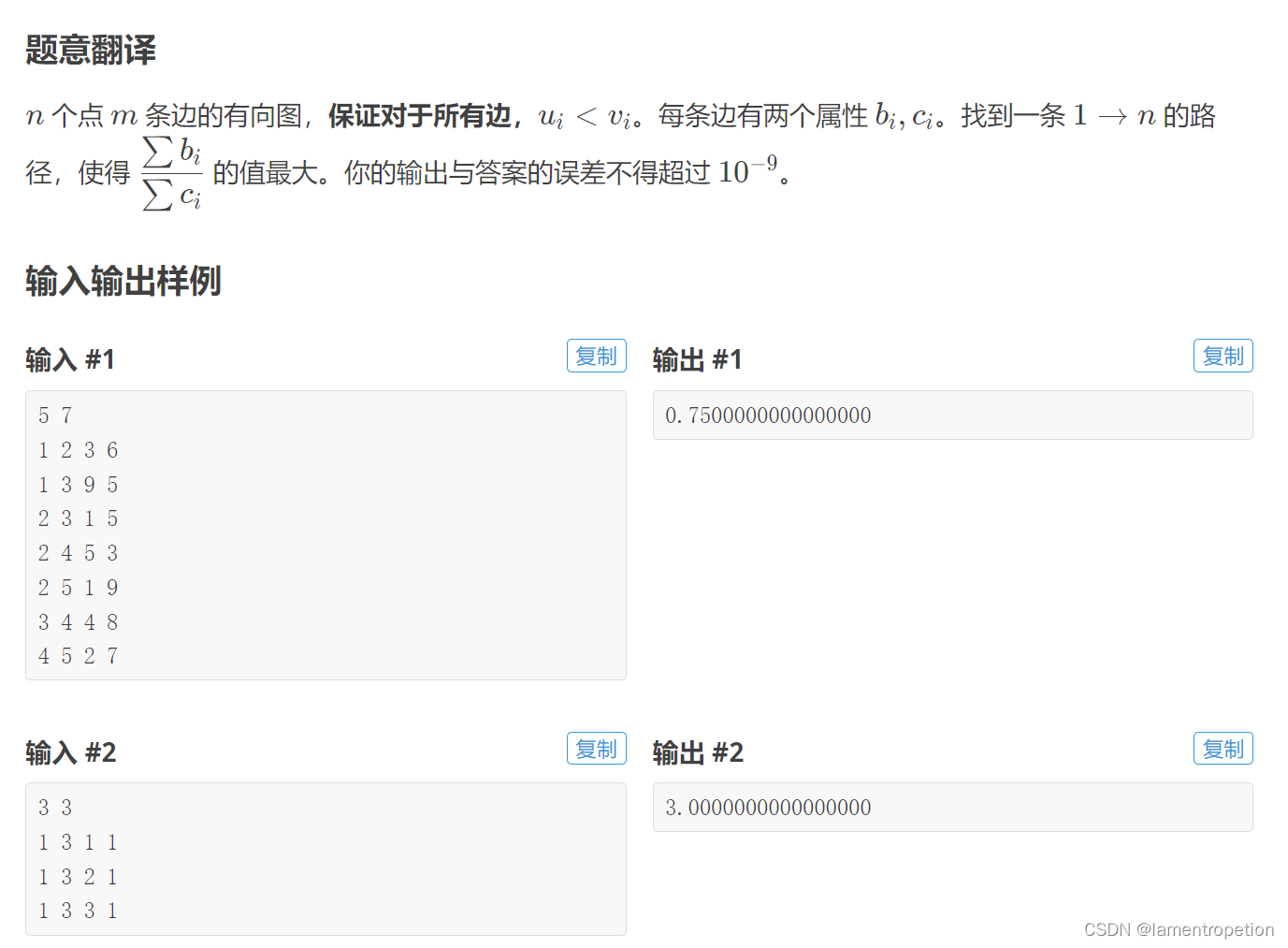
首先看到这个形式很容易想到 01 分数规划，即去二分答案，然后就是转化成 是否存在一个路径使得 sigma b - mid * sigma c >= 0

显然只需要改变一下边权，跑一遍最长路即可

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define double long double
const int N = 200200;
const double eps = 1e-15;
int n, m;
int deg[N];
struct Edge {
    int nxt;
    int to;
    int w1;
    int w2;
    Edge() {}
    Edge(int x, int y, int w, int z)
        : nxt(x), to(y), w1(w), w2(z) {}
} e[N << 2];
int h[N], cnt;
void add(int u, int v, int w1, int w2) {
    e[++cnt] = Edge(h[u], v, w1, w2);
    h[u] = cnt;
    return;
}
double L = 0, R = 2e17;
double mx[N];
bool check(double x) {
    for (int i = 1; i <= n; ++i) {
        mx[i] = -2e17;
    }
    mx[1] = 0;
    for (int u = 1; u <= n; ++u) {
        for (int i = h[u]; i; i = e[i].nxt) {
            int v = e[i].to;
            double w1 = e[i].w1, w2 = e[i].w2;
            mx[v] = max(mx[v], mx[u] + w1 - x * w2);
        }
    }
    if (mx[n] >= 0)
        return 1;
    return 0;
}
signed main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; ++i) {
        int u, v, w1, w2;
        scanf("%d%d%d%d", &u, &v, &w1, &w2);
        add(u, v, w1, w2);
        deg[v]++;
    }
    while (R - L > eps) {
        double mid = (L + R) / 2.0;
        if (check(mid)) {
            L = mid;
        } else {
            R = mid;
        }
    }
    printf("%.18Lf\n", L);
    return 0;
}