激活函数是非线性的函数，使用它的原因就是因为线性函数无论叠加多少层，最终带来的变化都是线性的组合，一般也只能用于线性分类，如经典的多层感知机。但是如果加上非线性的变换，根据通用近似定理，就可使得神经网络无限逼近任意函数，可以解决的问题范围也就大大增加了。此外激活函数对于加快模型收敛、缓解梯度消失等问题也大有帮助。下面举例3个常见的激活函数，sigmoid、tanh、relu及其变种。

激活函数都是非线性的；连续并且可导（用于反向传播算法）；尽可能的简单；值域在一个小的区间。

---

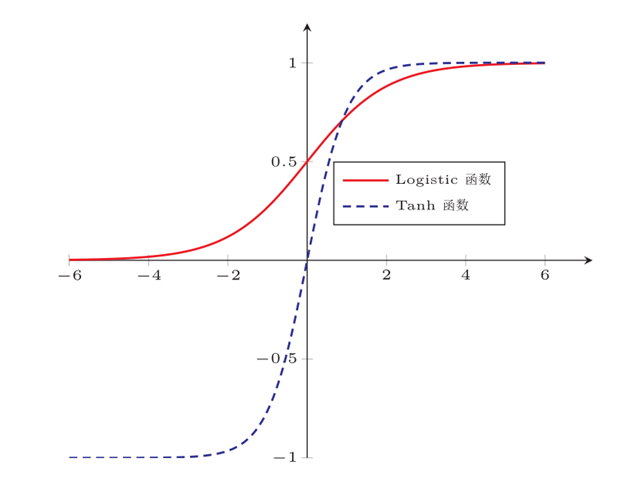
1.sigmoid函数与tanh函数

sigmoid也叫logistics函数它的输出恒大于0如图所示，值域是在0-1的。所以它可以把特征值压缩到较小的范围，使得训练结果比较问题波动不会太大。缺点是导数即梯度值可能过于接近0，随着梯度的传播，导数越来越接近0，最终导致梯度消失的问题。此外，输出不是0均值，进而导致后一层神经元将得到上一层输出的非0均值的信号作为输入。随着网络的加深，会改变原始数据的分布趋势；

而Tanh函数是零中心化，可以解决sigmoid输出不是0均值的问题；同时它的导数范围比sigmoid大，所以可以稍微缓解梯度消失的问题，但是仍然存在。

2者都属于饱和函数，容易导致梯度消失问题

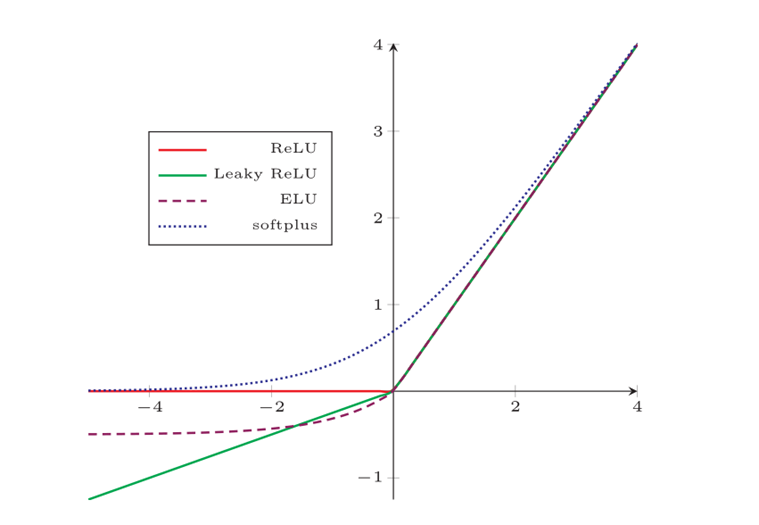
2.relu及其变种

relu属于非饱和函数，在输入为正时，导数不会趋近0，所以梯度消失问题大大缓解

但是它输出不是0均值，且有因为没有趋于0的导数，由于数据的不同可能导致梯度爆炸问题