感谢梦翔老哥的蓝桥杯C++ AB组辅导课~
省一刷200题 国赛拿成绩300题
比赛考察的是各种模型的熟练度,可以从dfs的角度比较各个模型与当前问题的匹配程度。
常见时间复杂度,根据时间复杂度可以判别是否可以选用这个解题思路

写递归的时候,可以考虑将递归写成递归搜索树的形式,比较便于理解:

常见的数字:

递归实现指数型枚举:

递归的思路就是找到一个顺序不重不漏的遍历所有情况。本题的思路就是遍历每个位置,考虑每个位置选或不选的情况。

ac代码:
从第0个位置开始枚举,到第n-1的位置。先写边界,边界写完可以考虑上面图中的某个节点(红圈),设置某个位置的数字后递归回溯要还原现场。
递归是怎么实现回溯的呢?看下列代码,dfs(u+1)的位置,执行到此处代码会进入到新的函数当中,当dfs(u+1)执行结束的时候,会跳转到目前执行的下一行,为了不影响“选”的决策,需要把位置设置为原来的0。建议与上面的红圈图搭配着看比较清晰。
其实本题可以不用恢复现场,并且state[u] = 0 会被state[u] = 1 和下次dfs中的status[u]=2覆盖掉,因为最后输出只在递归树的末端,此时所有的位置都是1或者2,没有0。
递归实现排列型枚举:
做递归题建议先把递归搜索树写出来,明确思路。会简单很多。

思路1:枚举每个数字放到哪个位置 × 由于题目要求输出字典序较小的数字,模拟了一下发现不能满足题目要求。
思路2:枚举每个位置放哪个数字 √
递归搜索树
AC代码:

时间复杂度分析:
根据递归搜索树分析,第一层O(n),第二层nxn,第三层nx(n-1)xn... 视频后面还有个证明,大概是使用了放缩,将红框的内容全部加起来,提出来个n,剩余的部分可以放缩成小于等于3倍的n!。所以最终的时间复杂度为nxn!。
习题1:
递归实现组合型枚举

思路:
一开始看到这个题,感觉跟例题里的枚举每个位置放哪个数基本一致,以为稍微改一下数组大小就行。但题意要求输出升序序列。所以在这基础上需要进行剪枝,123是可以的,132就是不行的。所以在填写位置的时候,将目前已经填写的数字(3)与即将要填入的数字(2)进行比较,如果已经填写的数字大于即将填入的数字,那就不能填,再往后看看有没有合适的数。
AC代码:
#include<bits/stdc++.h>
using namespace std;
vector<int> ans;
bool state[26];
int m,n; //m表示位置个数,n表示数字个数
void dfs(int u){//枚举位置
if(u == m){
for(int i=0;i<m;i++){
cout<<ans[i]<<" ";
}
cout<<endl;
return;
}
int num = -1;
for(int i=1;i<=n;i++){
if(ans.size()!=0){
num = ans[ans.size()-1];
}
if(!state[i]&&(i>num)){
ans.push_back(i);
state[i] = true;
dfs(u+1);
ans.pop_back();
state[i] = false;
}
}
}
int main(){
cin>>n>>m;
dfs(0);
return 0;
}习题2:带分数

自己没想出来,引用一下人家的题解(没想到竟然如此暴力):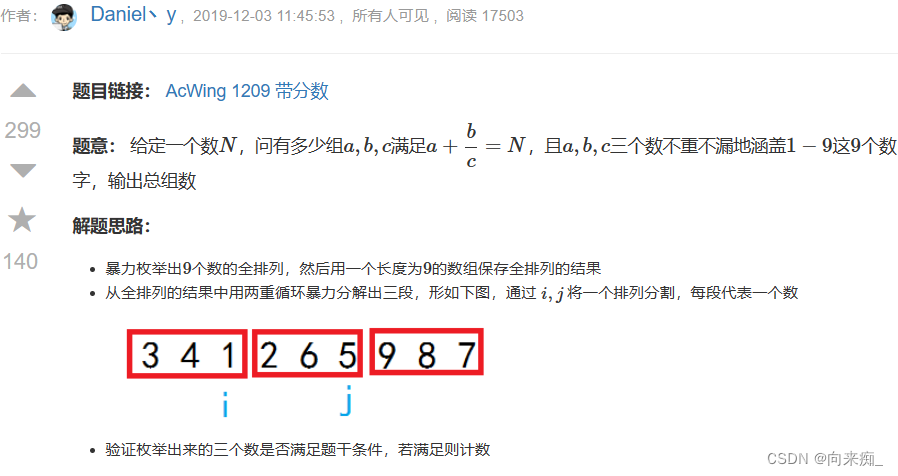
代码如下(代码自己想着敲得):
#include<bits/stdc++.h>
using namespace std;
vector<int> ans;
bool status[10];
int cnt = 0;
int calc(int i,int j){
int num = ans[i];
while(i<j){
i++;
num = num*10 + ans[i];
}
return num;
}
void dfs(int u,int target){
if(u == 9){
//对ans进行处理,走到这里正好凑够9位
for(int i=0;i<7;i++){ //这里注意循环到7
for(int j = i+1;j<8;j++){ //这里注意循环到8 不然没有c这个数了
int a = calc(0,i);
// printf("%d",a); wc加了个printf就超时了
int b = calc(i+1,j);
int c = calc(j+1,8);
if((a*c+b) == (target * c)) cnt++;
}
}
return;
}
for(int i=1;i<=9;i++){
if(!status[i]){
ans.push_back(i);
status[i] = true;
dfs(u+1,target);
status[i] = false;
ans.pop_back();
}
}
}
int main(){
int n;
scanf("%d",&n);
dfs(0,n);
printf("%d",cnt);
return 0;
}