一、算法介绍.

计算某一点到直线的距离，这里的直线会用2个点来表示，如果你只有直线上一点和直线的方向向量，应该也可以转为2个点
（代码复制粘贴即可使用，需要注意的是，这里是直线，不是线段，要区分好，
而且只是二维的，要计算三维的可以参考 点到空间直线的四种距离计算方法）

二、算法实现

1.代码

#include <iostream>
using namespace std;

struct Point {
    float x, y;
};

int main() {

    Point p1 = { 0, 0 };
    Point p2 = { 4, 0 };

    Point p = { -2, -6 };


    double dis = abs((p1.y - p2.y) * (p.x - p2.x) - (p.y - p2.y) * (p1.x - p2.x))/sqrt(pow(p2.y - p1.y, 2) + pow(p2.x - p1.x,2));
    cout << "点到直线的距离为： " << dis << endl;

    system("pause");
    return 0;
}

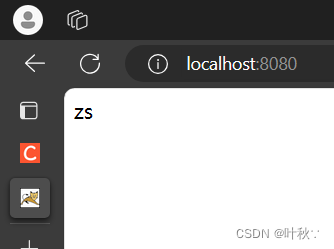
2.结果

---

总结

仅限二维场景使用

分子为0时，表示点到直线的距离为0