回溯算法

1、简介

简介：回溯法也可以叫做回溯搜索法，它是一种搜索的方式。

• 回溯是递归的副产品，只要有递归就会有回溯。
• 回溯是一种暴力的搜索方式。

回溯法，一般可以解决如下几种问题：组合（无序）、排列（有序）

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等等
  • 组合是不强调元素顺序的，排列是强调元素顺序。
  • 例如：{1, 2} 和 {2, 1} 在组合上，就是一个集合，因为不强调顺序，而要是排列的话，{1, 2} 和 {2, 1} 就是两个集合了。

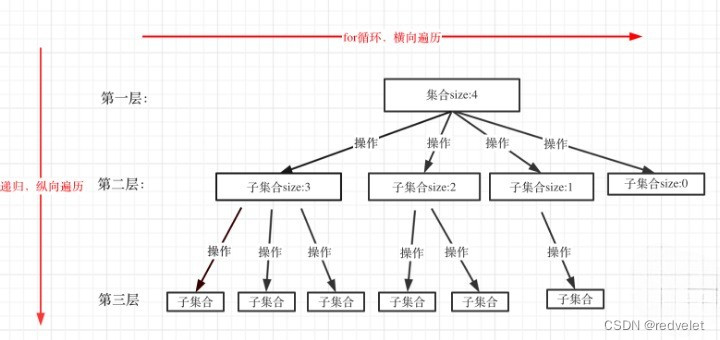
回溯模板：回溯过程可以抽象为一颗n叉树

• 这颗抽象的树形结构中，每一个节点都是一个for循环，for循环的起始位置是从startIndex开始，然后遍历剩余元素

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

2、核心问题

🚀解题流程：

1. 确定递归函数的参数和返回值
2. 确定递归的终止条件
3. 确立单层递归的逻辑

---

🚀回溯问题：

1. 收集结果在哪？是叶子节点收集结果还是路径收集？-> return的位置和是否需要
2. 去重在哪去重？树层还是树枝？相邻元素如何去重？不相邻元素如何去重？-> 相邻和hash
3. 组合问题、子集问题、排列问题的区别在哪？
4. 有序和无序的区别是什么？

3、例题

题目：给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案

1. 确定参数：ArrayList path存放单个组合、ArrayList result存放所有组合结果、n，k确定组合和范围、startIndex确定下次搜索的起始位置
2. 确定终止条件：单个组合path大小为k，收集结果
3. 确立单层递归逻辑：for循环开始为startIndex，递归遍历，下一层起始位置为startIndex+1，弹出元素回溯。

public List<List<Integer>> combine(int n, int k) {
    //1.确定参数和返回值
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    int startIndex = 1;
    backtracking(result, path, n, k, startIndex);

    //返回结果
    return result;
}

public void backtracking(List<List<Integer>> result, List<Integer> path, int n, int k, int startIndex) {
    //2.确立递归终止条件
    if (k == path.size()) {
        result.add(new ArrayList<>(path));
        return;
    }

    //3.确立单层递归逻辑
    for (int i = startIndex; i <= n; i++) {
        path.add(i);
        backtracking(result, path, n, k, i + 1);
        path.remove(path.size() - 1);
    }
}