目录

一、Logistic函数

二、前馈神经网络（FNN）

三、反向传播算法（BP算法）

​四、基于前馈神经网络的手写体数字识别

---

一、Logistic函数

Logistic函数是学习前馈神经网络的基础。所以在介绍前馈神经网络之前，我们首先来看一看Logistic函数。

Logistic函数定义为：

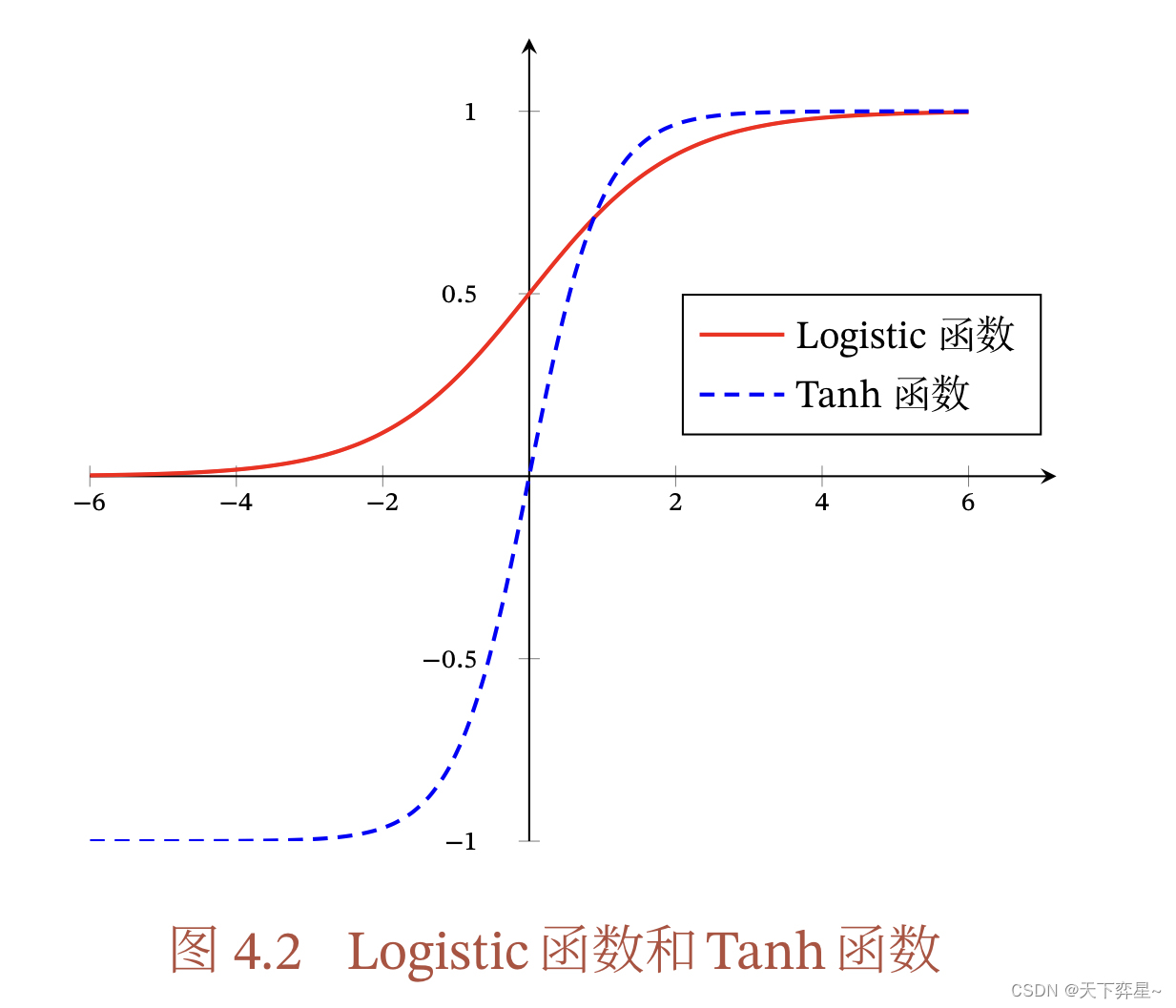
Logistic函数可以看成是一个“挤压”函数， 把一个实数域的输入“挤压”到(0,1)。当输入值在0附近时。Sigmoid型函数近似为线性函数；当输入值靠近两侧时，对输入进行抑制。输入越小，越接近于0；输入越大，越接近于1。

这样的特点也和生物神经元类似，对一些输入会产生兴奋（输入为1），对另一些输入产生抑制（输出为0）。和感知器使用的阶跃激活函数相比，Logistic函数是连续可导的，其数学性质更好。

因为Logistic函数的性质，使得装备了Logistic激活函数的神经元具有以下两点性质：

（1）其输出直接可以看作概率分布，使得神经网络可以更好地和统计学习模型进行结合；

（2）其可以看作一个软性门，用来控制其他神经元输出信息的数量。

Logistic函数的导数为，其推导过程如下：

Logistic函数的图像如下：

二、前馈神经网络（FNN）

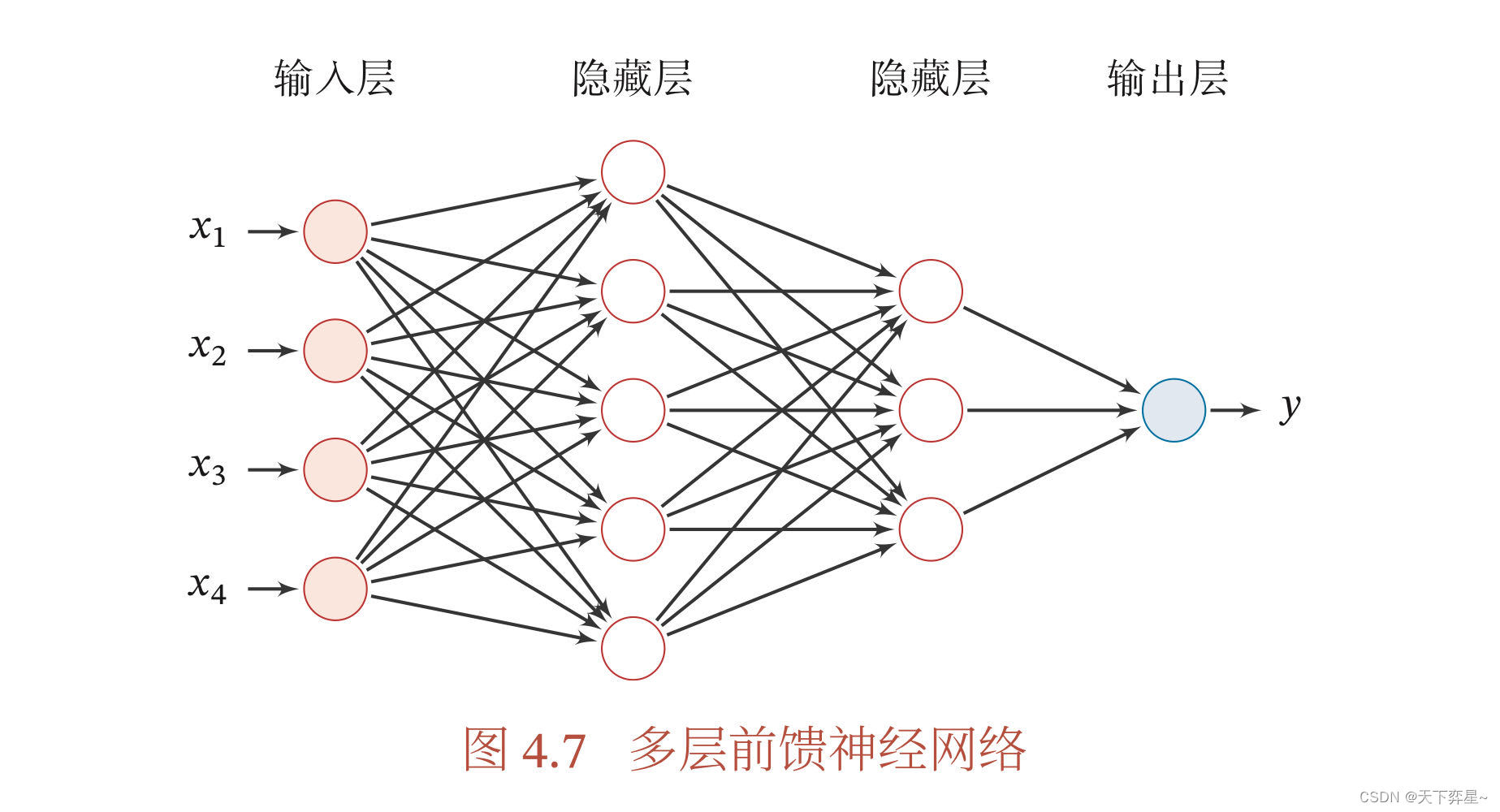
前馈神经网络其实是由多层的Logistic回归模型（连续的非线性函数）组成，而不是由多层的感知器（不连续的非线性函数）组成。

在前馈神经网络中， 各神经元分别属于不同的层。每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层。第0层称为输入层，最后一层称为输出层，其他中间层称为隐藏层。整个网络中无反馈，信号从输入层向输出层单向传递，可用一个有向无环图表示。

接下来，我们以下面的一个神经网络为例，推导前馈神经网络的数学模型。

图中，代表第j层第i个神经元的活性值，代表控制激活函数从第j层映射到第j+1层的权重矩阵。 

这里的激活函数我们使用的是Logistic函数，这里我们用g(x)表示。

因此，有：

 

 

 

 

 

 

 

 

 

 

 

我们也可以将上面的公式写成向量的形式：

 

 

 

因此，该前馈神经网络最后的输出值为：

                     

                              

                                    

                                           

                                                 

                                                          

可以看出，这是一个复合函数。

三、反向传播算法（BP算法）

这里，我们还是使用上面的神经网络模型：

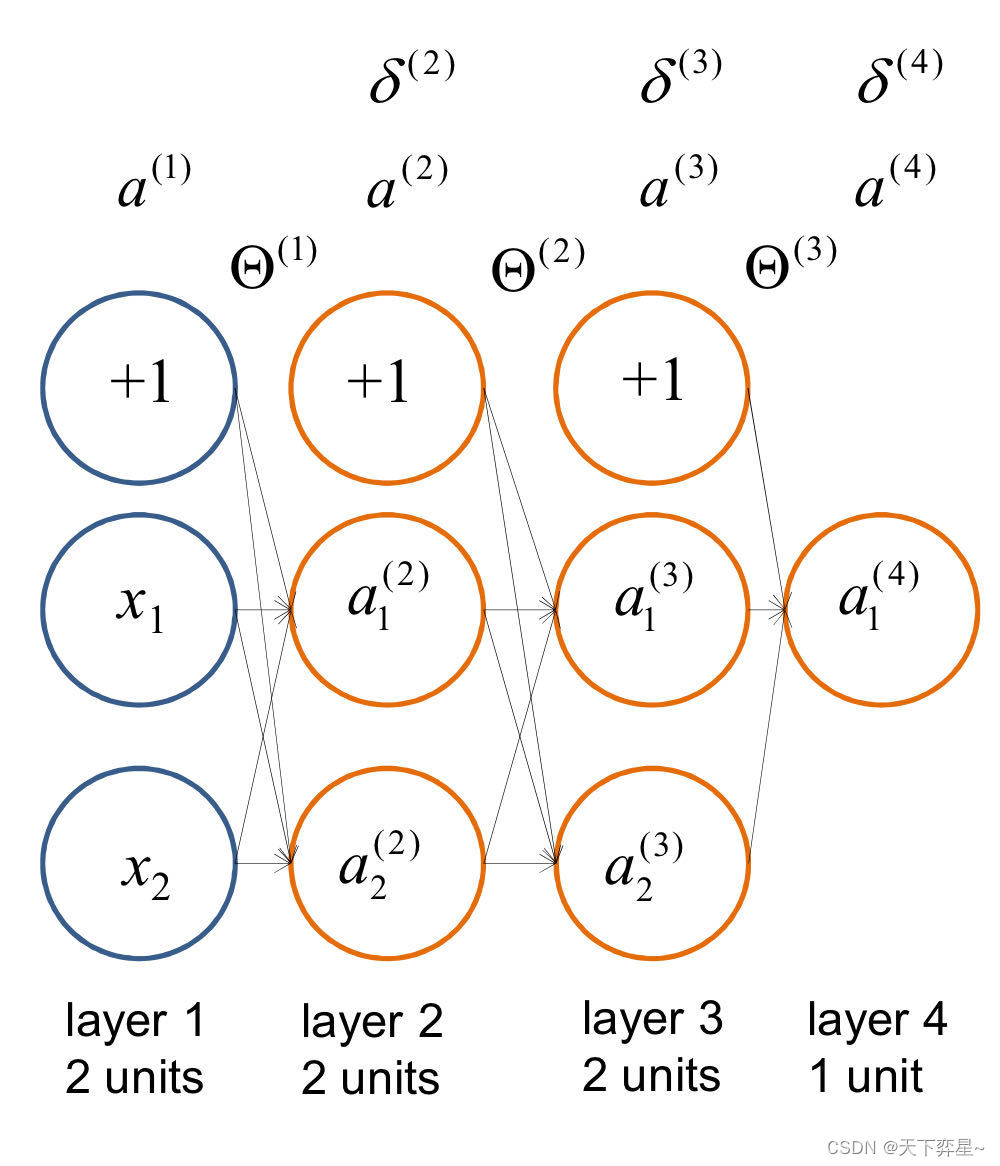
这里，代表第l层第j个神经元的误差。

该神经网络的损失函数为：

这里，我们令 ，并且有，在不考虑正则项的情况下，有：

 于是，反向传播算法的推导过程如下：

首先，令

（=预测值-真实值） 

根据链式求导法则有：

由于 

故

 

由于

故

 

              

              

              

              

              

因此，

接下来，我们先来推导一下：

首先，

根据链式求导法则，有：

 

已知，

又由于

 

故有：

因此，有：

 

接着，再推导：

 

已知 ，，

又由于

故有：

 

因此，有：

 

下面继续推导 :

由链式求导法则有：

已知 ，，

又由于

 

故有：

因此， 

接着，继续推导：

由链式求导法则有：

已知 ，，，

又由于

故有：

 

因此，

 

                                                   

                                                   

综上，有：

 

因此，有：

四、基于前馈神经网络的手写体数字识别

首先查看手写体数据集情况：

from scipy.io import loadmat

data=loadmat("C:\\Users\\LEGION\\Documents\\Tencent Files\\215503595\\FileRecv\\hw11data.mat")
X=data['X']
y=data['y']
print('X type:',type(X))
print('X shape:',X.shape)
print('y type:',type(y))
print('y shape:',y.shape)

X type: <class 'numpy.ndarray'>
X shape: (5000, 400)
y type: <class 'numpy.ndarray'>
y shape: (5000, 1)

接着，从数据集中随机选取100行并转化成图片：

from random import sample
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

'''随机选取100行'''
r=[int(i) for i in range(5000)]
R=sample(r,100)
X_choose=np.zeros((100,400))
for i in range(100):
    X_choose[i,:]=X[R[i],:]
    
'''将随机选取的100行数据分别转换成20X20的矩阵形式'''
X_matrix=[X_choose[i].reshape([20,20]).T for i in range(100)]

'''转换成图片'''
fig=plt.figure()
for i in range(100):
    ax=fig.add_subplot(10,10,i+1)
    ax.imshow(X_matrix[i],interpolation='nearest')
plt.show()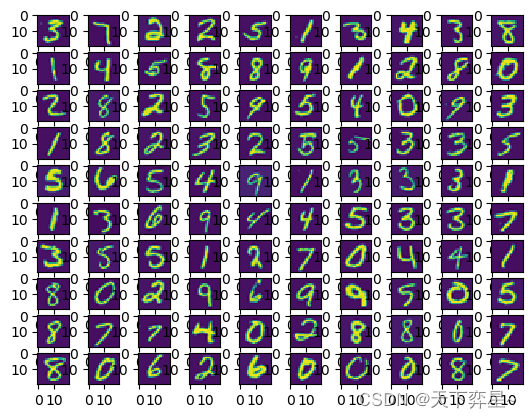

查看已经训练好的权重数据集情况：

from scipy.io import loadmat

weights=loadmat("C:\\Users\\LEGION\\Documents\\Tencent Files\\215503595\\FileRecv\\hw11weights.mat")
theta1=weights['Theta1']
theta2=weights['Theta2']
print('theta1 tyep:',type(theta1))
print('theta1 shape:',theta1.shape)
print('theta2 type:',type(theta2))
print('tehta2 shape:',theta2.shape)

theta1 tyep: <class 'numpy.ndarray'>
theta1 shape: (25, 401)
theta2 type: <class 'numpy.ndarray'>
tehta2 shape: (10, 26)

计算前馈神经网络对手写体数字识别的准确率：

'''添加元素1'''
X0=X.tolist()
for i in range(5000):
    X0[i].insert(0,1)
X1=np.array(X0)

'''进行神经网络的第一层计算'''
Z1=[]   #5000 date of second layer
for i in range(5000):
    a=np.dot(theta1,X1[i].T)
    z1=(a.T).tolist()
    Z1.append(z1)

'''计算逻辑函数值'''
Y1=[]
for i in range(5000):
    y0=[]
    for j in range(25):
        b=1/(1+np.exp(-Z1[i][j]))
        y0.append(b)
    Y1.append(y0)


'''添加元素1'''
for i in range(5000):
    Y1[i].insert(0,1)
Y2=np.array(Y1)

'''进行神经网络的第二层计算'''
Z2=[]   #5000 date of third layer
for i in range(5000):
    a=np.dot(theta2,Y2[i].T)
    z2=(a.T).tolist()
    Z2.append(z2)
    
'''计算逻辑函数值'''
Y2=[]
for i in range(5000):
    y0=[]
    for j in range(10):
        c=1/(1+np.exp(-Z2[i][j]))
        y0.append(c)
    Y2.append(y0)
    
'''转换成输出值'''
Y=[]
for i in range(5000):
    s=Y2[i].index(max(Y2[i]))
    Y.append(s+1)
    
'''计算神经网络预测的准确率'''
n=0
for i in range(5000):
    if y[i]==Y[i]:
        n+=1
pre_ratio=n/5000
print("神经网络预测的准确率：{}".format(pre_ratio))

神经网络预测的准确率：0.9752

计算损失函数值：

from scipy.io import loadmat
import numpy as np


'''读取数据'''
data=loadmat("C:\\Users\\LEGION\\Documents\\Tencent Files\\215503595\\FileRecv\\hw11data.mat")
X=data['X']
y=data['y']

weights=loadmat("C:\\Users\\LEGION\\Documents\\Tencent Files\\215503595\\FileRecv\\hw11weights.mat")
theta1=weights['Theta1']
theta2=weights['Theta2']


#进行神经网络运算
'''添加元素1'''
X0=X.tolist()
for i in range(5000):
    X0[i].insert(0,1)
X1=np.array(X0)

'''进行神经网络的第一层计算'''
Z1=[]   #5000 date of second layer
for i in range(5000):
    a=np.dot(theta1,X1[i].T)
    z1=(a.T).tolist()
    Z1.append(z1)

'''计算逻辑函数值'''
Y1=[]
for i in range(5000):
    y0=[]
    for j in range(25):
        b=1/(1+np.exp(-Z1[i][j]))
        y0.append(b)
    Y1.append(y0)


'''添加元素1'''
for i in range(5000):
    Y1[i].insert(0,1)
Y2=np.array(Y1)

'''进行神经网络的第二层计算'''
Z2=[]   #5000 date of third layer
for i in range(5000):
    a=np.dot(theta2,Y2[i].T)
    z2=(a.T).tolist()
    Z2.append(z2)
    
'''计算逻辑函数值'''
Y2=[]
for i in range(5000):
    y0=[]
    for j in range(10):
        c=1/(1+np.exp(-Z2[i][j]))
        y0.append(c)
    Y2.append(y0)
    
'''转换成输出值'''
Y=[]
for i in range(5000):
    s=Y2[i].index(max(Y2[i]))
    Y.append(s+1)
    
#计算损失函数值
cost=0
for i in range(5000):
    cost0=0
    d=[0 for i in range(10)]
    d[y[i][0]-1]=1
    for j in range(10):
        p=d[j]*np.log(Y2[i][j])+(1-d[j])*np.log(1-Y2[i][j])
        cost0=cost0+p
    cost=cost+cost0
cost=cost*(-1/5000)
print("损失函数值：{}".format(cost))

损失函数值：0.2876291651613188