推荐系统中，ID类特征的表示学习（embedding learning）是深度学习模型成功的关键，因为这些embedding参数占据模型的大部分体积。这些模型标准的做法是为每一个ID特征分配一个unique embedding vectors，但这也导致存储embedding table需要消耗巨大的内存。

在上一篇文章中 Embedding压缩之hash embedding，介绍了几种常见的hash embedding方法来对embedding进行压缩，实现模型的瘦身。今天继续介绍一种阿里在CIKM 2021的论文中提出的方法：基于二进制码的hash embedding，该方法兼具了调整embedding存储的大小的灵活性和尽可能保留模型的效果。

算法流程

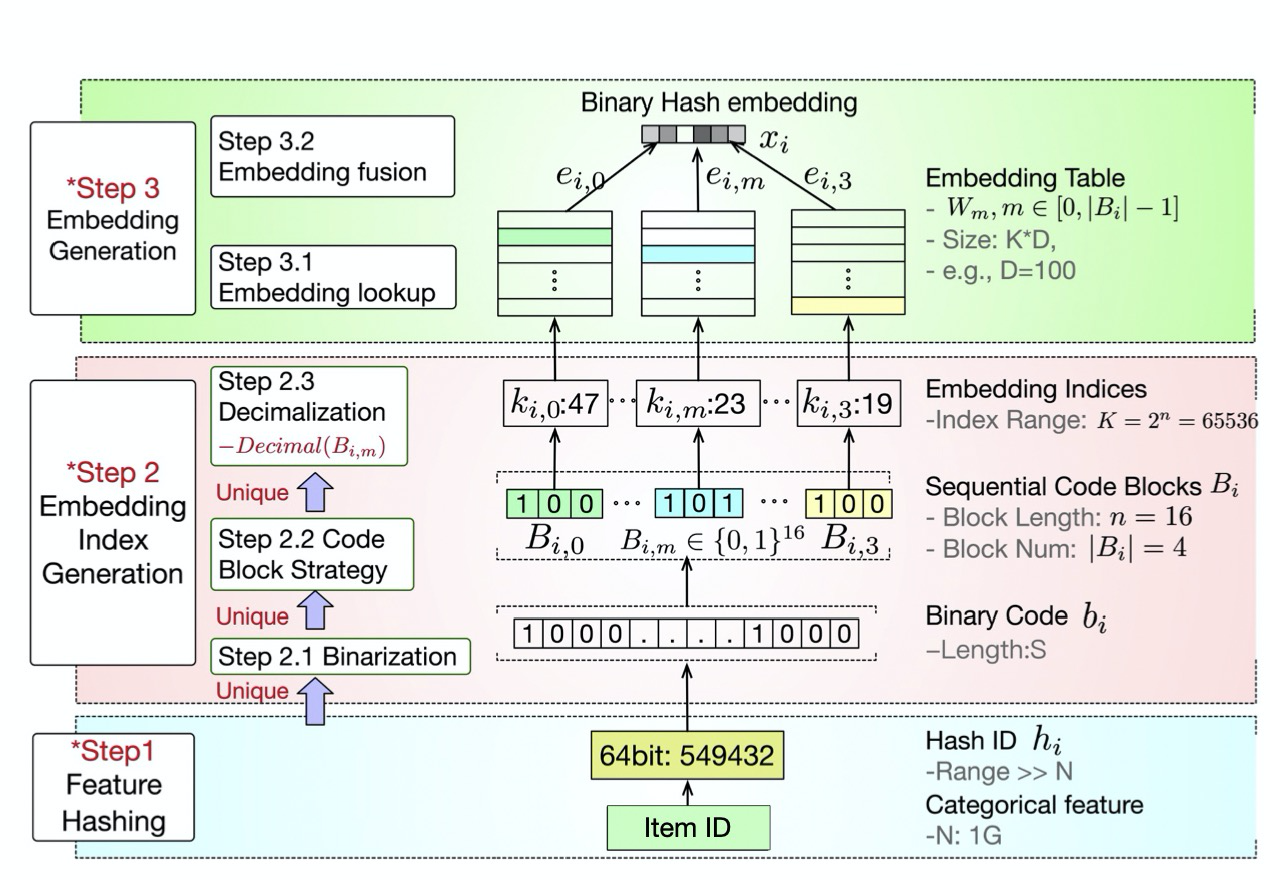
Binary code based Hash Embedding的算法流程如下图，主要分为了3步：特征hash、embedding索引生成、embedding向量生成。

特征Hash

ID类特征的来源是多种类型，比如字符串或者整型，实际中的做法分为两种：

1. 提前创建映射表，即将不同的特征值映射到对应的unique id，这种做法的缺点是不灵活，难以应对特征值的动态扩展，并且需要保存映射表；
2. 另一种做法则是使用特征Hash，可以直接将原始特征值映射到Integer，如上图[Binary Hash Embedding-Step1]，称为Hash ID：

$h_i=\mathcal{H}(f_i)$

其中，$\mathcal{H}$为hash函数（如Murmur Hash），$h_i$为特征值$f_i$的Hash ID。为了尽量降低$h_i$之间的冲突，$\mathcal{H}$的输出通常是一个比较大的数值，比如64位的Integer。

embedding索引生成

如上图[Binary Hash Embedding-Step2]，Embedding索引生成分为3步：Binarization、Code Block Strategy和Decimalization。

Binarization

在特征Hash之后，每一个特征值可以认为是拥有一个对应的唯一(没有冲突)的Hash ID。

在这一步，会将Hash ID转化为一个二进制码 b i ∈ { 0 , 1 } S b_i \in \{0,1\}^S bi​∈{0,1}S，S为二进制码的长度，如上图[Binary Hash Embedding-Step2.1]，比如13的二进制码是$1101_2$。

因为10进制转2进制这个过程是不包含任何参数，并且计算逻辑是固定的，因此二进制码$b_i$是可以与特征值$f_i$一一对应的。

Code Block Strategy

前面提到基于二进制码的hash embedding在调整embedding存储大小上具备灵活性，这个灵活性在这一节就会得到体现。论文提出了一种策略 code block strategy：

1. 将二进制码$b_i$的每一个0-1值切分到不同的块(blocks)，每一个block中有序的0-1码可以来表示 $K=2^n$ 个不同的整数，其中n是每个block中0-1值的个数，如上图[Binary Hash Embedding-Step2.2]。
2. 接着，再将每一个block的0-1码转换成10进制的整数，作为每一个block的embedding table $W\in {\mathbb{R}}^{K\times D}$的索引。

比如，当n=1时，每个block的0-1值个数为2，embedding table的存储大小为$O(2D)$。而当所有的0-1值放在同一个block的时候，此时就相当于full embedding。因此，embedding table的大小可以通过n来控制，这也正是这个策略的灵活性体现。

用表达式来看，定义$B_i=[B_{i,0};B_{i,1};...;B_{i,m};...]$为code block strategy产出的block序列，$|B_i|$是block的数量，那么第m个block B i , m ∈ { 0 , 1 } n B_{i,m} \in \{0,1\}^n Bi,m​∈{0,1}n可以表示为下式：

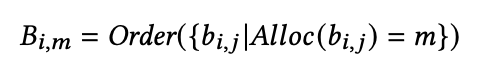
其中，Alloc是一个分配函数，将每一个0-1值分配到不同的block。Order则是将每个block的0-1值变为有序的函数。

论文提出了两种code block strategy的形式：

• Succession. 如下图[code block strategy-a]，succession策略从左往右遍历，Alloc函数会会将每t个0-1值放入到同一个block。而Order函数则是保持$b_i$中每一个0-1值的原有顺序。
• Skip. 如下图[code block strategy-b]，skip策略将间隔为t的0-1值放入同一个block。Order函数与succession策略相同。
• 当最后剩余的0-1值不够t时，则会将剩下的所有0-1值放入到同一个block中。

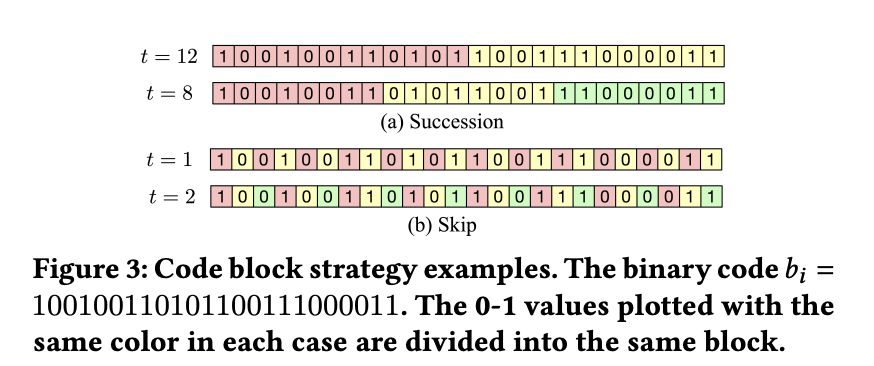
通过code block strategy，对于每一个$b_i$可以获得唯一的$B_i$。但其实如果Hash ID长度空间超过$2^S$，那么还是会产生冲突的。

Decimalization

每一个block的embedding索引$k_{i,m}$则通过$B_{i,m}$的十进制得到，如上图[Binary Hash Embedding-Step2.3]：

$k_{i,m}=Decimalize(B_{i,m})$

其实就是将block中的0-1二进制码转化为10进制，作为embedding索引。

embedding向量生成

Embedding Lookup. 如上述提到，每一个block $B_{i,m}$可以得到一个embedding索引$k_{i,m}$，那么就可以将$k_{i,m}$映射到一个embedding向量

$e_{i,m}=\epsilon (W_m,k_{i,m})$

$W_m$是第m个block $B_{i,m}$对应的embedding table，$e_{i,m}$则代表$B_{i,m}$的embedding，而$\epsilon$是embedding lookup函数。

Embedding Fusion. 通过上面的流程，可以得到$|B_i|$个embedding，最后需要将$|B_i|$个embedding进行组合得到特征值 $f_i$ 最终的embedding $x_i$，组合形式一般包括Sum Pooling、LSTM、Concatenation。

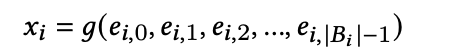
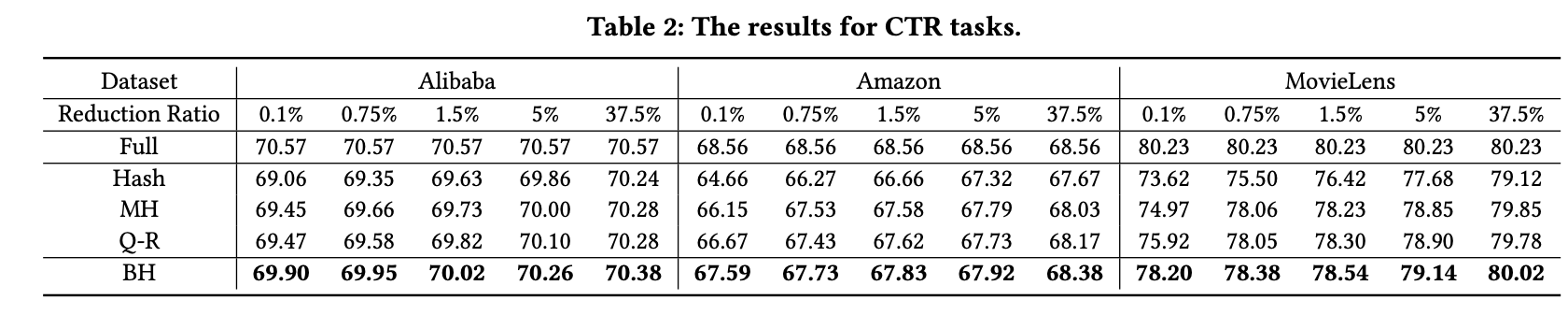
实验结果

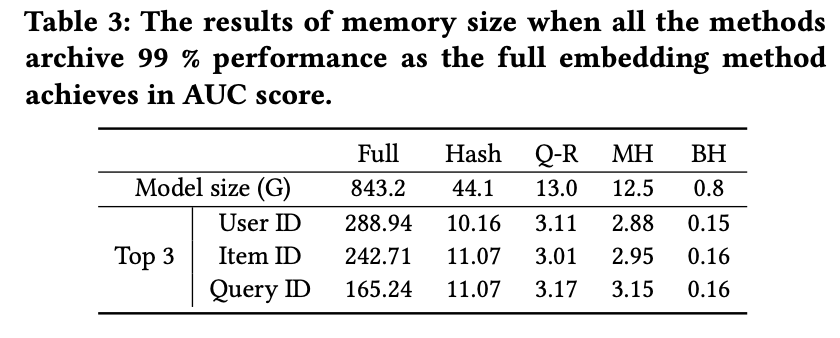
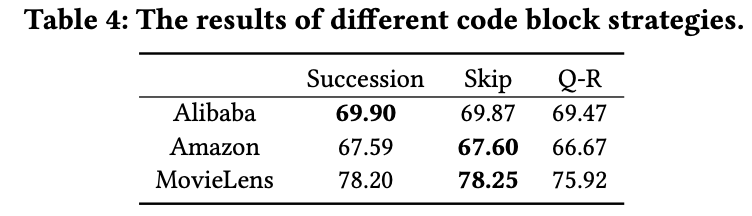
总结

优势

• 确定性。embedding索引的计算是一个确定性的无参数的过程，对于新的特征值是友好的。
• 灵活性。embedding的存储大小是靠超参数n来调整的。
• 唯一性。无论embedding缩减到什么程度，每一个特征值$f_i$都有唯一的$B_i$（在Hash ID长度空间不超过$2^S$的前提下）
• 压缩率高。假如Hash ID的长度空间为$2^{24}$，那么full embedding的存储大小为$2^{24}\times D$。而如果选择策略为succession，且t=12，即block的数量为 $24/12=2$，每个block的0-1个数为12，那么基于二进制码的hash embedding存储大小为$2\times 2^{12}\times D$，压缩率高达$1/2^{11}$。

对比

• Full Embedding：Full Embedding与论文方法都很好区分不同的特征值，该论文方法能够很好减少embedding的存储；
• Hash Embedding：是论文方法的一种简化形式，即code block strategy是Succession，且仅取前t个0-1值来计算embedding索引；
• Multi-Hash Embedding：都可以创建多个embedding索引，但论文方法对这些索引的唯一性约束更好；
• Q-R Trick：可以看作是论文方法的一种特例，code block strategy是Succession，前t个0-1码作为quotient，剩余的0-1码作为remainder。

最后，再总结下基于二进制码的Hash Embedding原理。

1. 将特征值的Hash ID转化为二进制码；
2. 然后将二进制码的0-1值切分到不同的block，每一个block对应一个embedding table；
3. 而每一个block中的0-1二进制码转换回10进制作为embedding索引；
4. 最后，将从每一个block得到的embedding进行组合作为最后的embedding表征。

代码实现

git

包括二进制码的Hash编码算子实现、二进制码的Hash Embedding的Python实现。