文章目录
- 问题描述
- Python调用OR-Tools建模求解(实验一)
- 1. 声明问题的模型
- 2. 创建区间变量
- 3. 创建约束条件
- 4. 求解模型
- 5. 基于 plotly 展示甘特图
- 不同场景下的求解效率对比
- 实验二:工件的工序数有差异
- 实验三:消除工件的加工时长差异
- 实验三与实验一的对比分析
相关文章:
《【作业车间调度JSP】通过python调用PuLP线性规划库求解》
《【作业车间调度JSP】通过python调用OR-Tools的区间变量建模求解》
问题描述
JSP(Job Shop Scheduling Problem)问题是指车间作业调度问题,是生产调度领域中的经典问题之一。JSP问题涉及到一组工件(Jobs)和一组机器(Machines),每个工件都有一系列工序需要在不同的机器上完成,每个工序有一个特定的加工时间。通过确定每个工件的工序顺序和在每台机器上的开始时间,以最优化既定的目标。这个问题的复杂性(NP-Hard问题)和实际应用的广泛性使得研究和优化JSP一直是运筹学和制造业领域的热点。
在前面的相关文章中,仅测试了小规模的算例,例如只有 6 个工件,且每个工件仅 6 个工序。在大规模问题下,有些求解器的求解时间急剧增加,有些求解器仍然表现出很有优势的性能,因此,本文通过更大规模的算例进行实验。
基于 Hurink-sdata 数据集中算例 abz7.fjs 进行实验,具体的算例数据解析可以参考文章《解析FJSP问题的标准测试数据集的Python代码》,该JSP算例有 20 个待加工工件,15台机器,每个工件有15道工序,总共的工序一共有300步。以最小化全部工件的完工时间为目标。
Python调用OR-Tools建模求解(实验一)
对于JSP问题而言,最基本的约束有两块:(1)工件的工序需按顺序加工,前序工序加工完才能加工后续工序;(2)机器加工的不重叠性,即机器在同一时间只能完成一个加工任务。
特别的,OR-Tools具有关于区间变量的特定约束,即去重叠。因此,本文基于OR-Tools的区间变量进行建模求解,验证区间变量在这类带顺序的模型(VRP/JSP…)中的效果。通过《解析FJSP问题的标准测试数据集的Python代码》当中的代码进行解析。
1. 声明问题的模型
OR-Tools 的 cp_model 在建模之前需要先声明问题的模型。
import collections
from ortools.sat.python import cp_model
model = cp_model.CpModel()
2. 创建区间变量
在这里,区间变量指每个任务的加工时间段,即机器被某道工序占用的时间段,当工序在机器上的加工时间固定时,这个区间变量的长度 duration 也固定,进一步地,当工序的开始加工时间固定,则相对应的结束时间也固定。
对每个工序都要建立一个区间变量,而区间变量的基本元素包括,工序的开始加工时间(变量),结束加工时间(变量),加工时长(常量)。为了尽量减少可行解空间大小,开始时间和结束时间的上界尽可能紧凑,这里我们取所有工序的加工时长之和作为时间变量的上界。
# 命名元组:存储变量信息(相当于实例化一道工序)
task_type = collections.namedtuple("task_type", "start end interval")
# 存储所有工序信息
all_tasks = {}
# 将工序信息按可上机器(一台)进行存储
machine_to_intervals = collections.defaultdict(list)
# 时间变量的上界
horizon = sum(job_step_machine_2_ptime[job] for job in job_step_machine_2_ptime)
for job_id in range(Job_num):
for task_id in range(job_2_step_num[job_id]):
machine_ = job_step_2_avail_machines[job_id, task_id][0]
duration = job_step_machine_2_ptime[job_id, task_id, machine_]
suffix = f"_{job_id}_{task_id}_{duration}"
start_var = model.NewIntVar(0, horizon, "start" + suffix)
end_var = model.NewIntVar(0, horizon, "end" + suffix)
interval_var = model.NewIntervalVar(
start=start_var, size=duration, end=end_var, name="interval" + suffix)
all_tasks[job_id, task_id] = task_type(
start=start_var, end=end_var, interval=interval_var)
machine_to_intervals[machine_].append(interval_var)
上述创建变量的代码中,先创建了 start_var 和 end_var 变量,然后将这两个变量传入模型的函数NewIntervalVar以创建区间变量。其中,当区间变量内指定了end后,则默认end变量的值与start变量的值的差距为duration。
然后将创建的变量存储进 all_task 字典,并按工序的可上机器存储到 machine_to_intervals 字典。
注意:OR-Tools的CP-SAT求解器支持的基础变量类型只有整数型变量(包括布尔变量),因此对时间变量时创建为整数变量,可通过系数的方式来控制变量精度。
3. 创建约束条件
在OR-Tools中,有专门针对区间变量的约束AddNoOverlap,即指定若干区间变量之间彼此不重叠,但无先后关系保证,这类约束成为不相容约束(Disjunctive constraints),在JSP问题中体现在,机器在同一时间只能加工一个任务(暂不考虑批量加工),此时需要约束同一机器上的区间变量彼此之间不重叠。
约束1:机器上的加工工序不能重叠(不相容约束)
for machine in machine_to_intervals:
model.AddNoOverlap(machine_to_intervals[machine])
约束2:每个工件内的待加工工序具有先后顺序。
for job_id in range(Job_num):
for task_id in range(job_2_step_num[job_id]-1):
model.Add(all_tasks[job_id, task_id + 1].start >= all_tasks[job_id, task_id].end)
约束3:最大完工时间等于所有工序完工时间的最大值。
obj_var = model.NewIntVar(0, horizon, "makespan")
model.AddMaxEquality(obj_var, [all_tasks[index].end for index in all_tasks])
model.Minimize(obj_var)
4. 求解模型
OR-Tools的CP-SAT需要模型先创建求解器,再调用Solve()函数进行求解。
solver = cp_model.CpSolver()
status = solver.Solve(model)
打印求解结果:
print(f"Optimal Schedule Length: {solver.ObjectiveValue()}")
print("\nStatistics")
print(f" - conflicts: {solver.NumConflicts()}")
print(f" - branches : {solver.NumBranches()}")
print(f" - wall time: {solver.WallTime()}s")
由于求解时间较长(>5 min),因此求解达到终止条件时(Gap<5%)就返回当前可行解,之后可行解在向最优解步进时Gap的收敛速度急剧下降。
Optimal Schedule Length: 685.0
Statistics
- conflicts: 3388
- branches : 7498
- wall time: 5.044260157s
5. 基于 plotly 展示甘特图
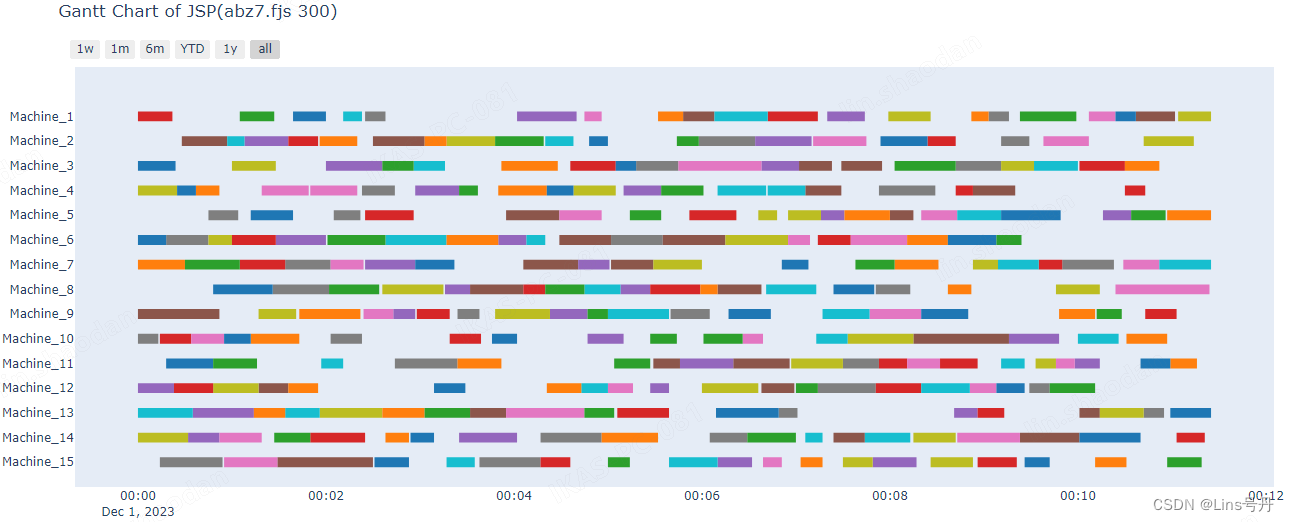
甘特图是查看车间调度问题方案的最直观形式,基于上面的求解结果画的甘特图如下:
import datetime
import plotly.figure_factory as ff
j_record = {}
for job_id in range(Job_num):
for task_id in range(job_2_step_num[job_id]):
start_ = solver.Value(all_tasks[job_id, task_id].start)
start_time=str(datetime.timedelta(seconds=start_))
machine_ = job_step_2_avail_machines[job_id, task_id][0]
duration = job_step_machine_2_ptime[job_id, task_id, machine_]
end_time=str(datetime.timedelta(seconds=start_+duration))
j_record[(machine_, job_id)]=[start_time,end_time]
gantt_data = []
for machine_ in range(1, Machine_num+1):
for job_ in range(Job_num):
if (machine_, job_) in j_record:
gantt_data.append(
dict(Task=f"Machine_{machine_}", Start=f"2023-12-01 {str(j_record[machine_, job_][0])}",
Finish=f"2023-12-01 {str(j_record[machine_, job_][1])}", Resource=f"Job_{job_}")
)
fig = ff.create_gantt(gantt_data, index_col='Resource', group_tasks=True, show_colorbar=False, title="Gantt Chart of JSP(Mk10 240)")
fig.show()
该求解结果的甘特图中,不展示图例的原因是该plotly库默认只有十种颜色的条形图,而本案例中的工件有20个,感兴趣的可以在库方法
create_gantt中增加新的颜色。
不同场景下的求解效率对比
基于上述的求解结果,现在提出一个问题,即不同的工序分布是否会对求解效率有影响。
由于 JSP 问题的极度非凸的特性,可能很难去证明这种分布对效率的影响关系,但可以通过一些实验对特殊情况下的效率变化进行简单的判断。
实验二:工件的工序数有差异
为了保证可比性,这里的实验基于上述的 abz7.fjs 数据进行修改,在大部分的标准测试数据中工件的工序数都是相等的。这里我们对不等长的工艺流程问题进行求解效率的对比。
直观的,我们将一部分工件的工序移到另一部分工件工序的末尾,可以达到目的。然而,值得注意的是,若把每个工件的工序当成独立的色块,则不论如何修改这些工序所在的工件,问题的求解规模貌似没有变化,但是这部分往后移的工序的最早开工时间就会受到限制,总体目标值会更大。除此之外,还会有其他的变化吗?
调整后的数据如下:
20 15 1
16 1 3 24 1 4 12 1 10 17 1 5 27 1 1 21 1 7 25 1 9 27 1 8 26 1 2 30 1 6 31 1 12 18 1 15 16 1 14 39 1 11 19 1 13 26 1 1 36
17 1 7 30 1 4 15 1 13 20 1 12 19 1 2 24 1 14 15 1 11 28 1 3 36 1 6 26 1 8 15 1 1 11 1 9 23 1 15 20 1 10 26 1 5 28 1 13 17 1 7 15
18 1 7 35 1 1 22 1 14 23 1 8 32 1 3 20 1 4 12 1 13 19 1 11 23 1 10 17 1 2 14 1 6 16 1 12 29 1 9 16 1 5 22 1 15 22 1 5 15 1 10 32 1 11 16
19 1 10 20 1 7 29 1 2 19 1 8 14 1 13 33 1 5 30 1 1 32 1 6 21 1 12 29 1 11 24 1 15 25 1 3 29 1 4 13 1 9 20 1 14 18 1 3 21 1 14 20 1 10 33 1 4 27
20 1 12 23 1 14 20 1 2 28 1 7 32 1 8 16 1 6 18 1 9 24 1 10 23 1 4 24 1 11 34 1 3 24 1 1 24 1 15 28 1 13 15 1 5 18 1 5 23 1 14 40 1 11 12 1 7 23 1 8 27
21 1 9 24 1 12 19 1 15 21 1 2 33 1 8 34 1 7 35 1 6 40 1 11 36 1 4 23 1 3 26 1 5 15 1 10 28 1 14 38 1 13 13 1 1 25 1 4 36 1 3 29 1 2 18 1 12 13 1 7 33 1 13 13
22 1 14 27 1 4 30 1 7 21 1 9 19 1 13 12 1 5 27 1 3 39 1 10 13 1 15 12 1 6 36 1 11 21 1 12 17 1 2 29 1 1 17 1 8 33 1 12 36 1 5 12 1 11 33 1 15 19 1 10 16 1 14 27 1 1 21
23 1 6 27 1 5 19 1 7 29 1 10 20 1 4 21 1 11 40 1 9 14 1 15 39 1 14 39 1 3 27 1 2 36 1 13 12 1 12 37 1 8 22 1 1 13 1 9 39 1 15 31 1 4 31 1 8 32 1 10 20 1 14 29 1 5 13 1 7 26
24 1 14 32 1 12 29 1 9 24 1 4 27 1 6 40 1 5 21 1 10 26 1 1 27 1 15 27 1 7 16 1 3 21 1 11 13 1 8 28 1 13 28 1 2 32 1 10 16 1 4 17 1 2 12 1 3 13 1 13 40 1 7 17 1 9 30 1 5 38 1 1 13
25 1 13 35 1 2 11 1 6 39 1 15 18 1 8 23 1 1 34 1 4 24 1 14 11 1 9 30 1 12 31 1 5 15 1 11 15 1 3 28 1 10 26 1 7 33 1 4 31 1 12 22 1 14 36 1 1 16 1 8 11 1 15 14 1 5 29 1 7 28 1 3 22 1 11 17
14 1 11 28 1 6 37 1 13 29 1 2 31 1 8 25 1 9 13 1 15 14 1 5 20 1 4 27 1 10 25 1 14 31 1 12 14 1 7 25 1 3 39
13 1 1 22 1 12 25 1 6 28 1 14 35 1 5 31 1 9 21 1 10 20 1 15 19 1 3 29 1 8 32 1 11 18 1 2 18 1 4 11
12 1 13 39 1 6 32 1 3 36 1 9 14 1 4 28 1 14 37 1 1 38 1 7 20 1 8 19 1 12 12 1 15 22 1 2 36
11 1 9 28 1 2 29 1 15 40 1 13 23 1 5 34 1 6 33 1 7 27 1 11 17 1 1 20 1 8 28 1 12 21
10 1 10 21 1 15 34 1 4 30 1 13 38 1 1 11 1 12 16 1 3 14 1 6 14 1 2 34 1 9 33
9 1 10 13 1 15 40 1 8 36 1 5 17 1 1 13 1 6 33 1 9 25 1 14 24 1 11 23
8 1 4 25 1 6 15 1 3 28 1 13 40 1 8 39 1 2 31 1 9 35 1 7 31
7 1 13 22 1 11 14 1 1 12 1 3 20 1 6 12 1 2 18 1 12 17
6 1 6 18 1 11 30 1 8 38 1 15 22 1 14 15 1 12 20
5 1 10 31 1 9 39 1 13 27 1 2 14 1 6 33
Optimal Schedule Length: 724.0
Statistics
- conflicts: 4400
- branches : 9376
- wall time: 5.084242107000001s
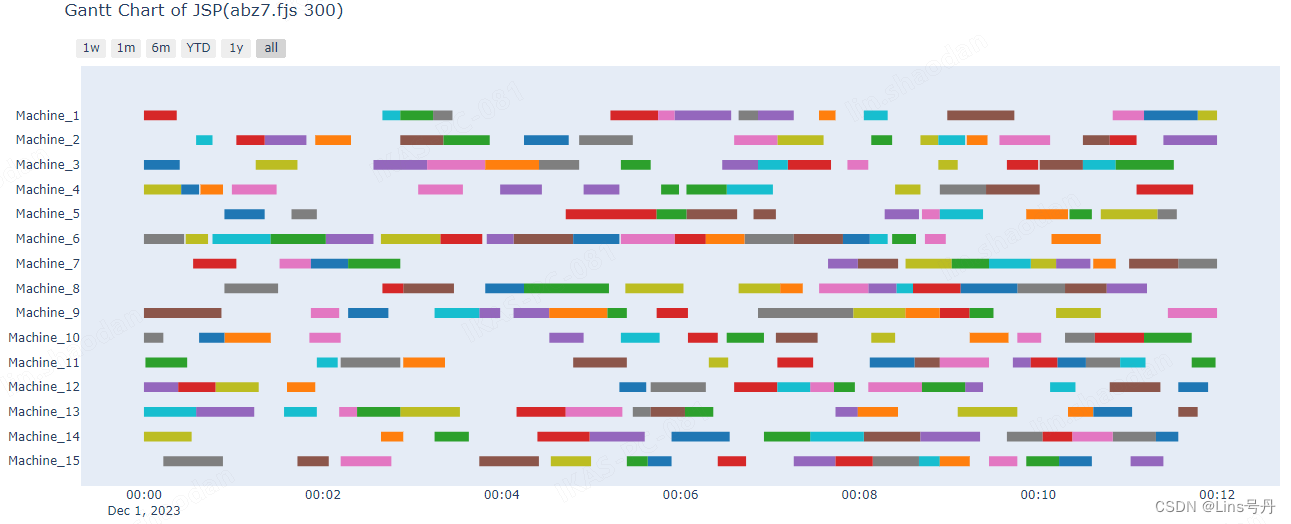
如上结果,在改变工序的工件分布情况后,求解的目标值比先前的实验目标更高,这符合我们的预期,就是部分工序的最早开工时间更晚,导致目标值会更高,且该问题下的方案会比前一个问题的方案的甘特图较稀疏,这些都是很直观的差异。
但是,在求解效率上,同样是收敛到 Gap<5%,实验二的多次求解的平均求解时间是显著短于实验一的,一方面可能是由于理论的最优目标值上升,导致的下界值更大,更快地达到Gap=5%,这个猜测很好理解且很合理。
实验三:消除工件的加工时长差异
但进一步地考虑,会不会是因为实验二将部分工件的部分工序移到了另一部分工件上,导致工件的总体加工时长不同导致的?现考虑新的实验,即在实验二数据的基础上,修改每个工件工序的加工时长,控制每个工件的工序总加工时长一致。
修改方式为仅修改最后一步的加工时长,以实验二中最大总加工时长的工件为基准,其他工件的最后一个工序的加工时长加上差值,以此消除不同工件之间加工时长的差异。数据如下:
20 15 1
16 1 3 24 1 4 12 1 10 17 1 5 27 1 1 21 1 7 25 1 9 27 1 8 26 1 2 30 1 6 31 1 12 18 1 15 16 1 14 39 1 11 19 1 13 26 1 1 258
17 1 7 30 1 4 15 1 13 20 1 12 19 1 2 24 1 14 15 1 11 28 1 3 36 1 6 26 1 8 15 1 1 11 1 9 23 1 15 20 1 10 26 1 5 28 1 13 17 1 7 263
18 1 7 35 1 1 22 1 14 23 1 8 32 1 3 20 1 4 12 1 13 19 1 11 23 1 10 17 1 2 14 1 6 16 1 12 29 1 9 16 1 5 22 1 15 22 1 5 15 1 10 32 1 11 247
19 1 10 20 1 7 29 1 2 19 1 8 14 1 13 33 1 5 30 1 1 32 1 6 21 1 12 29 1 11 24 1 15 25 1 3 29 1 4 13 1 9 20 1 14 18 1 3 21 1 14 20 1 10 33 1 4 186
20 1 12 23 1 14 20 1 2 28 1 7 32 1 8 16 1 6 18 1 9 24 1 10 23 1 4 24 1 11 34 1 3 24 1 1 24 1 15 28 1 13 15 1 5 18 1 5 23 1 14 40 1 11 12 1 7 23 1 8 167
21 1 9 24 1 12 19 1 15 21 1 2 33 1 8 34 1 7 35 1 6 40 1 11 36 1 4 23 1 3 26 1 5 15 1 10 28 1 14 38 1 13 13 1 1 25 1 4 36 1 3 29 1 2 18 1 12 13 1 7 33 1 13 77
22 1 14 27 1 4 30 1 7 21 1 9 19 1 13 12 1 5 27 1 3 39 1 10 13 1 15 12 1 6 36 1 11 21 1 12 17 1 2 29 1 1 17 1 8 33 1 12 36 1 5 12 1 11 33 1 15 19 1 10 16 1 14 27 1 1 120
23 1 6 27 1 5 19 1 7 29 1 10 20 1 4 21 1 11 40 1 9 14 1 15 39 1 14 39 1 3 27 1 2 36 1 13 12 1 12 37 1 8 22 1 1 13 1 9 39 1 15 31 1 4 31 1 8 32 1 10 20 1 14 29 1 5 13 1 7 26
24 1 14 32 1 12 29 1 9 24 1 4 27 1 6 40 1 5 21 1 10 26 1 1 27 1 15 27 1 7 16 1 3 21 1 11 13 1 8 28 1 13 28 1 2 32 1 10 16 1 4 17 1 2 12 1 3 13 1 13 40 1 7 17 1 9 30 1 5 38 1 1 42
25 1 13 35 1 2 11 1 6 39 1 15 18 1 8 23 1 1 34 1 4 24 1 14 11 1 9 30 1 12 31 1 5 15 1 11 15 1 3 28 1 10 26 1 7 33 1 4 31 1 12 22 1 14 36 1 1 16 1 8 11 1 15 14 1 5 29 1 7 28 1 3 22 1 11 34
14 1 11 28 1 6 37 1 13 29 1 2 31 1 8 25 1 9 13 1 15 14 1 5 20 1 4 27 1 10 25 1 14 31 1 12 14 1 7 25 1 3 297
13 1 1 22 1 12 25 1 6 28 1 14 35 1 5 31 1 9 21 1 10 20 1 15 19 1 3 29 1 8 32 1 11 18 1 2 18 1 4 318
12 1 13 39 1 6 32 1 3 36 1 9 14 1 4 28 1 14 37 1 1 38 1 7 20 1 8 19 1 12 12 1 15 22 1 2 319
11 1 9 28 1 2 29 1 15 40 1 13 23 1 5 34 1 6 33 1 7 27 1 11 17 1 1 20 1 8 28 1 12 337
10 1 10 21 1 15 34 1 4 30 1 13 38 1 1 11 1 12 16 1 3 14 1 6 14 1 2 34 1 9 404
9 1 10 13 1 15 40 1 8 36 1 5 17 1 1 13 1 6 33 1 9 25 1 14 24 1 11 415
8 1 4 25 1 6 15 1 3 28 1 13 40 1 8 39 1 2 31 1 9 35 1 7 403
7 1 13 22 1 11 14 1 1 12 1 3 20 1 6 12 1 2 18 1 12 518
6 1 6 18 1 11 30 1 8 38 1 15 22 1 14 15 1 12 493
5 1 10 31 1 9 39 1 13 27 1 2 14 1 6 505
Optimal Schedule Length: 1763.0
Statistics
- conflicts: 132
- branches : 861
- wall time: 0.2170565s
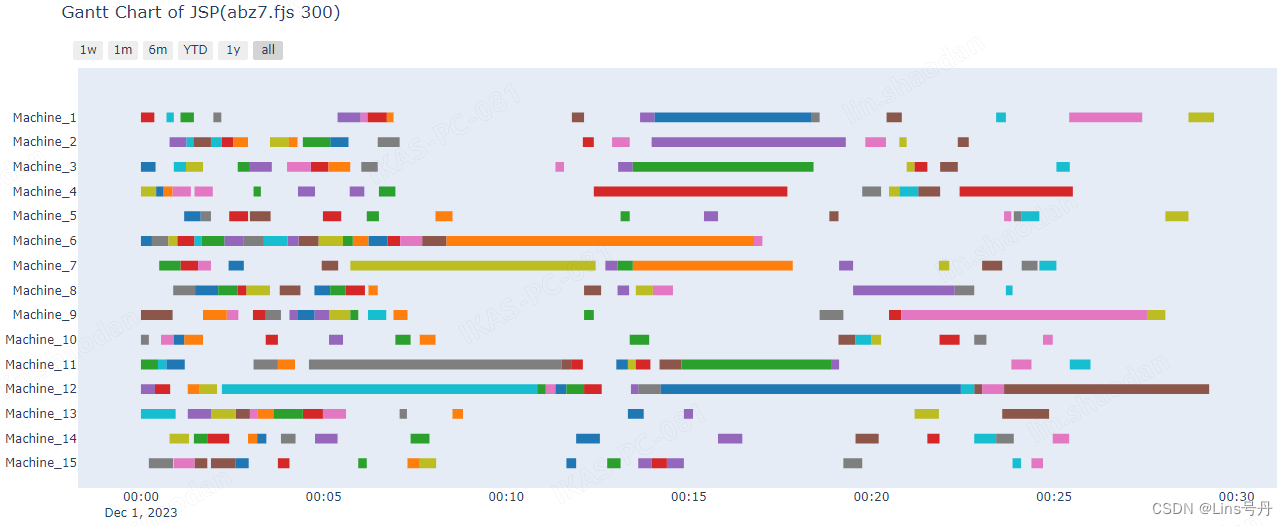
结果发现,实验三平均求解0.2s左右的时间,Gap就收敛到5%以内,实验二到实验三的差距仅在统一了每个工件的总加工时长,带来的求解效率差距显著,由此可见,工序数对求解效率的影响可能更多地是由于工序的开工时间晚导致目标下限提高,进而减少了Gap收敛到5%以内的时间。而真正对求解时间有巨大影响的因素来自统一工序加工时长而改变的深层次原因。
实验三的求解时间缩短了二十多倍,而目标值提高不到3倍,由此可见是由于某些因素的改变导致的求解结构的变化,进而极大地改变了求解效率。
实验三与实验一的对比分析
对于实验三的效率急剧提升,我们进行猜测,难道工序的总工序加工时间保持一致?就能提高求解效率?假设实验三每个工件的工序都在同一台机器上加工,显然该猜测不成立,因为此时不论最后一步的加工时长多长,问题的求解规模是完全不变的。
而之所以实验三有极大的效率变化,是因为工件的工序处在不同的机器上加工,因此我们进一步猜测,这种求解收敛的效率,受到不同设备的可上工序的总加工时长的影响,时长差异越大,则求解收敛效率越高。从直观地理解来看,当瓶颈工序,瓶颈设备显著,则目标值的优化空间会限制在关键工序上,此时整体问题的收敛效率高。
根据实验二和实验三的数据调整可知,实验三数据中机器的可加工工序数与实验一一致,不发生改变,因此比较实验一和实验三的可加工工序的总时长,如下:
# 实验一
{1: 428, 2: 497, 3: 525, 4: 464, 5: 454, 6: 549, 7: 530, 8: 530, 9: 498, 10: 443, 11: 461, 12: 447, 13: 501, 14: 556, 15: 483}
方差:1660.2095238095237
# 实验三
{1: 778, 2: 780, 3: 783, 4: 930, 5: 454, 6: 1021, 7: 1150, 8: 670, 9: 869, 10: 443, 11: 1101, 12: 1737, 13: 565, 14: 556, 15: 483}
方差:116802.38095238095
因此可知,JSP 问题中。设备上的可加工工序的总时长的差异越大,则问题的收敛效率越高,而工序在不同工件上的分布,以及工件的工序数、工件的工序总加工时长等并不很决定性的因素(引起的求解效率的变化不足以支撑它是关键因素)。