[CQOI2014] 危桥
题目描述
Alice 和 Bob 居住在一个由 \(N\) 座岛屿组成的国家,岛屿被编号为 \(0\) 到 \(N-1\)。某些岛屿之间有桥相连,桥上的道路是双向的,但一次只能供一人通行。其中一些桥由于年久失修成为危桥,最多只能通行两次。
Alice 希望在岛屿 \(a_1\) 和 \(a_2\) 之间往返 \(a_n\) 次(从 \(a1\) 到 \(a2\) 再从 \(a2\) 到 \(a1\) 算一次往返)。同时,Bob 希望在岛屿 \(b_1\) 和 \(b_2\) 之间往返 \(b_n\) 次。这个过程中,所有危桥最多通行两次,其余的桥可以无限次通行。请问 Alice 和 Bob 能完成他们的愿望吗?
输入格式
本题有多组测试数据。
每组数据第一行包含七个空格隔开的整数,分别为\(N\)、\(a_1\)、\(a_2\)、\(a_n\)、\(b_1\)、\(b_2\)、\(b_n\)。
接下来是一个 \(N\) 行 \(N\) 列的对称矩阵,由大写字母组成。矩阵的 \(i\) 行 \(j\) 列描述编号 \(i-1\) 和 \(j-1\) 的岛屿间的连接情况,若为 “O” 则表示有危桥相连:为 “N” 表示有普通的桥相连:为 “X” 表示没有桥相连。
输出格式
对于每组测试数据输出一行,如果他们都能完成愿望输出 “Yes”,否则输出 “No”(不含引号)。
样例 #1
样例输入 #1
4 0 1 1 2 3 1
XOXX
OXOX
XOXO
XXOX
4 0 2 1 1 3 2
XNXO
NXOX
XOXO
OXOX样例输出 #1
Yes
No提示
对于所有数据,\(4 \leq N\leq 50,\ 0 \leq a_1, a_2, b_1, b_2 \leq N-1,\ 1 \leq a_n, b_n \leq 50\)。
一个显然的思路:把图建出来后,源点向 \(a_1\) 连 \(a_n\) 流量,\(a_2\) 向汇点连 \(a_n\) 流量。\(b\) 同理。然后你会发现会出现 \(a_1\) 向 \(b_2\) 流的情况,所以满流不代表答案为 Yes
然后有结论:源点向 \(b_2\)连边,\(b_1\) 向汇点连边的情况下,如果还是满流,答案一定为 Yes
证明?看下图: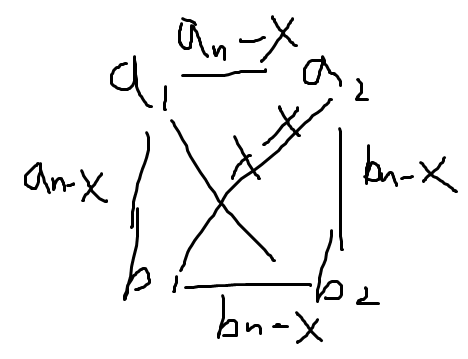
d当中如果两次都满流,大致的流向是这样子,此时如果 \(a_1\) 到 \(b_2\) 有流量,那么 \(a_1->b_1->a_2\) 就是一个符合要求的流。
#include<bits/stdc++.h>
using namespace std;
const int N=55,M=3005;
struct edge{
int v,nxt,f;
}e[M];
int e_num,f[M],hd[N],vh[N],a0,a1,an,b0,b1,bn,l,r,v[N],q[N],n;
void add_edge(int u,int v,int f)
{
e[++e_num]=(edge){v,hd[u],f};
hd[u]=e_num;
}
int bfs()
{
memcpy(vh,hd,sizeof(hd));
memset(v,0,sizeof(v));
v[q[l=r=1]=0]=1;
while(l<=r)
{
for(int i=hd[q[l]];i;i=e[i].nxt)
if(e[i].f&&!v[e[i].v])
v[q[++r]=e[i].v]=v[q[l]]+1;
++l;
}
return v[n+1];
}
int dfs(int x,int fl)
{
if(x==n+1)
return fl;
int k;
for(int&i=vh[x];i;i=e[i].nxt)
{
if(v[e[i].v]==v[x]+1&&e[i].f&&(k=dfs(e[i].v,min(fl,e[i].f))))
{
e[i].f-=k,e[i^1].f+=k;
return k;
}
}
return 0;
}
int dinic()
{
int k,ans=0;;
while(bfs())
{
while(k=dfs(0,1000000000))
ans+=k;
}
return ans;
}
int main()
{
while(scanf("%d%d%d%d%d%d%d",&n,&a0,&a1,&an,&b0,&b1,&bn)==7)
{
e_num=1;
memset(hd,0,sizeof(hd));
++a0,++a1,++b0,++b1;
for(int i=1;i<=n;i++)
{
char ch=getchar();
while(ch^'O'&&ch^'N'&&ch^'X')
ch=getchar();
for(int j=1;j<=n;j++)
{
if(i<=j)
{
if(ch=='O')
add_edge(i,j,1),add_edge(j,i,1);
if(ch=='N')
add_edge(i,j,1000000000),add_edge(j,i,1000000000);
}
ch=getchar();
}
}
add_edge(0,a0,an),add_edge(a0,0,0);
add_edge(a1,n+1,an),add_edge(n+1,a1,0);
for(int i=2;i<=e_num;i++)
f[i]=e[i].f;
int l0=hd[0],lb0=hd[b0],lb1=hd[b1],lbn=hd[n+1];
add_edge(0,b0,bn),add_edge(b0,0,0);
add_edge(b1,n+1,bn),add_edge(n+1,b1,0);
if(dinic()!=an+bn)
{
puts("No");
continue;
}
e_num-=4;
for(int i=2;i<=e_num;i++)
e[i].f=f[i];
hd[0]=l0,hd[b0]=lb0,hd[b1]=lb1,hd[n+1]=lbn;
add_edge(0,b1,bn),add_edge(b1,0,0);
add_edge(b0,n+1,bn),add_edge(n+1,b0,0);
puts(dinic()==an+bn? "Yes":"No");
}
}