一、介绍

传统的监督学习是单标签学习，但是现实中一个实例可能对应多个标签。这篇文章介绍了多标签分类的定义和评价指标、多标签学习的算法还有其他相关的任务。

二、问题相关定义

2.1 多标签学习任务

假设$X=R^d$，表示d维的输入空间，$Y=(y_1,y_2,y_3.,...,y_q$表示输出的可能q个类别。多标签任务是学习一个方程，在训练集合$D=\{(x_i,Y_i)|1\le i\le m\}$学习一个X到Y的函数。对于每个多标签实例，$x_i\in X$是d维特征空间$(x_{i1},x_{i2},...,x_{id}{)}^T$，$Y_i\subseteq Y$是对应于$x$的标签几何。多标签学习任务就是学习一个多标签分类器$h(.)$，对于没有见到过的实例$x\in X$，可以预测他的标签$h(x)\subseteq Y$。

2.2 多标签学习的特点

2.2.1. 不同数据集多标签的程度可能不同

有几个有用的多标签指示符可以用于描述多标签数据集的特性。

• 最自然的方法就是衡量多标签程度的是label cardinality(标签基数）：
  $$LCard(D)=\frac{1}{m}\sum _{i=1}^m|Y_i|$$
  表示每个样本的平均标签数目。
• “标签密度”（label density）按标签空间中可能的标签数规范化标签基数：
  $$LDen(D)=\frac{1}{y}\cdot LCard(D)$$
• 标签多样性：Label diversity
  $$LDiv(D)=|Y|existsx:(x,Y)\in D|$$
  数据集中出现的不同标签集的数目
• 标签多样性可以通过数据集的数量来标准化，以表示不同标签集的比例
  $$PLDiv(D)=\frac{1}{D}\cdot LDiv(D)$$
  多标签学习就是学习x和y的相关性，希望$f(x,y^{{}^{\prime }})\ge f(x,y^{{}^{\prime \prime }})$，其中$y^{\prime }\in Y$, $y^{{}^{\prime \prime }}\notin Y$。所以多标签分类器可以通过函数f(.,.)得到： h ( x ) = { y ∣ f ( x , y ) ≥ t ( x ) , y ∈ Y } h(x) = \{y | f(x,y) \ge t(x), y\in Y\} h(x)={y∣f(x,y)≥t(x),y∈Y}，其中$t(x)$，扮演阈值函数的角色，把标签空间对分成相关的标签集和不相关的标签集。阈值函数可以由训练集产生，可以设为常数。

2.2.2. 标签具有相互关系

学习策略
多标签学习的主要难点在于输出空间的爆炸增长，有效的挖掘标签之间的相关性，是多标签学习成功的关键。根据对相关性挖掘的强弱，可以把多标签算法分为三类。

1. 一阶学习策略：忽略和其它标签的相关性，比如把多标签分解成多个独立的二分类问题（简单高效）。
2. 二阶学习策略：考虑标签之间的成对关联，比如为相关标签和不相关标签排序。
3. 高阶学习策略：考虑多个标签之间的关联，比如对每个标签考虑所有其它标签的影响（效果最优）。

2.2.3 数据不平衡

一. 某个类别对应样例可能远多于另一个类别，类别之间不平衡
二. 某个类别对应的正样本可能远多于负样本（类别之内不平衡）

2.3 阈值校准

多标签学习中的一种常见做法是返回一些实值函数$f（\cdot ，\cdot ）$作为学习模型。为了决定最后的输出结果，每个标签上的实值输出应根据阈值函数输出$t(x)$进行校准。
通常有两种方法设置$t(\ast )$，设置$t(\ast )$为常量或者从训练数据中预测。对于前者，$f$是一个实值函数，所以t可设置为0。当$f$的输出为概率时，$t$设置为0.5。或者当测试集可见时，阈值可以设置为训练集合测试集的多标签程度指标区别最小的数。
对于后一个策略，可以用stacking-style的步骤来决定阈值函数。假设$t$是一个线性模型，即$t(x)=<w,f(x)>+b$，这里$f(x)=(f(x,y1),...,f(x,y_q){)}^T\in R^q$是一个$q$维stacking向量。为了学习$w^{\ast }$和$b^{\ast }$，需要求解线性最小二乘。
$$mi{n}_{w^{\ast },b^{\ast }}\sum _{i-1}^m(<w^{\ast },f^{\ast }(x_i)>+b^{\ast }-s(x_i){)}^2$$
s ( x i ) = a r g m i n a ∈ R ( ∣ { y j ∣ y j ∈ Y i , f ( x i , y j ) ≤ a } ∣ + ∣ { y k ∣ y k ∈ Y ^ i , f ( x i , y k ) ≥ a } ∣ ) s(x_i)=argmin_{a\in R}(|\{y_j | y_j \in Y_i, f(x_i, y_j) \leq a\}|+|\{y_k|y_k \in \hat Y_i, f(x_i, y_k) \geq a\}|) s(xi​)=argmina∈R​(∣{yj​∣yj​∈Yi​,f(xi​,yj​)≤a}∣+∣{yk​∣yk​∈Y^i​,f(xi​,yk​)≥a}∣)表示模型的输出目标，对每个样本，它以最小误差将$Y$划分为相关和不相关。

2.4 评价指标

2.4.1 分类评价指标

1. Examples-based metrics 基于样本评价指标
   通过分别评估学习系统在每个测试示例上的性能，然后返回整个测试集的平均值
2. Label-based metrics 基于标签评价指标
   通过分别评估每个类标签上的学习系统性能，然后返回所有类标签上的宏/微观平均值

2.4.2 排序评价指标

下面对每个指标进行介绍
基于样本的评价指标

1. Subset Accuracy(衡量正确率，预测的样本集和真实的样本集完全一样就是正确)
   $$subsetacc(h)=\frac{1}{p}\sum _{i=1}^p[h(x_i)=Y_i]$$
2. Hamming Loss（衡量的是错分的标签比例，正确标签没有被预测以及错误标签被预测的标签占比）
   $$hloss(h)=\frac{1}{p}\sum _{i=1}^p|h(x_i)\Delta Y_i|$$
   $\Delta$表示两个集合的对称差，返回只在其中一个集合出现的那些值。
3. Accuracy, Precision, Recall, F值（单标签学习中准确率，精准率，召回率，F值）
   $$Accuracy(h)=\frac{1}{p}\sum _{i=1}^p\frac{\mid h(x_i)\cap y_i\mid }{|h(x_i)\cup y_i|}$$
   $$Precision(h)=\frac{1}{p}\sum _{i=1}^p\frac{Y_i\cap h(x_i)}{h(x_i)}$$
   $$Recall=\frac{1}{p}\sum _{i=1}^p\frac{Y_i\cap h(x_i)}{Y_i}$$
   $$F=\frac{1+{\beta }^2\cdot Precision(h)\cdot Recall(h)}{{\beta }^2\cdot (Precision(h)+Recall(h))}$$
4. one-error(“预测到的最相关的标签” 不在 “真实标签”中的样本占比。值越小，表现越好)
   $$one-error(f)=\frac{1}{p}\sum _{i=1}^p[argma{x}_{y\in Y}f(x_i,y)\notin Y_i]$$
5. Coverage（值越小，表现越好)
   $$coverage(f)=\frac{1}{p}\sum _i^{p}ma{x}_{y\in Y_i}ran{k}_{f_{(}{x}_i,y)}-1$$
6. Ranking loss（值越小，表现越好)
   $$rloss(f)=\frac{1}{p}\sum _{i=1}^p\frac{1}{|Y_i||{\hat{Y}}_i|}|\{(y^{\prime },y^{{}^{\prime \prime }})|f(x_i,y^{\prime })\le f(x_i,y^{{}^{\prime \prime }}),(y^{\prime },y^{{}^{\prime \prime }})\in Y_i\times {\hat{Y}}_i\}|$$
7. Average Precision(度量比特定标签更相关的那些标签的排名的占比,越大越好)
   $$avgprec(f)=\frac{1}{p}\sum _{i=1}^p\frac{1}{|Y_i|}\sum _{y\in Y_i}\frac{|y^{\prime }|ran{k}_f(x,y^{\prime })\le ran{k}_f(x_i,y),y^{\prime }\in Y_i|}{ran{k}_{f(x_i,y)}}$$
   基于标签的评价指标
8. 分类评价指标
   对于每个标签，都可以得到$TP,FP,TN,FN$
   
   用$B(T{P}_j,F{P}_j,T{N}_j,F{N}_j)$表示特定的二元分类度量 B ∈ { A c c u r a c y , P r e c i s i o n , R e c a l l , F β } B \in \{Accuracy, Precision, Recall, F^{\beta}\} B∈{Accuracy,Precision,Recall,Fβ}，label-based的分类可以通过两种方式得到

• Macro-averaging(宏平均，先对单个标签下的数量特征计算得到常规指标，再对多个标签取平均)
  $$B_{macro(h)}=\frac{1}{q}\sum _{j=1}^{q}B(T{P}_j,F{P}_j,T{N}_j,F{N}_j)$$
• Micro-averaging(微平均，对数据集中的每一个实例不分类别进行统计建立全局混淆矩阵，然后计算相应指标）
  $$B_{micro(h)}=B(\sum _{j=1}^{q}T{P}_j,\sum _{j=1}^{q}F{P}_j,\sum _{j=1}^{q}T{N}_j,\sum _{j=1}^{q}F{N}_j)$$

9. 排序评价指标 rank metric

• AUC-macro（“排序正确”的数据对的占比,先对单个标签计算，再平均）
  $$AU{C}_{macro}=\frac{1}{q}\sum _{j=1}^{q}AU{C}_j=\frac{1}{q}\sum _{i=1}^q\frac{|\{(x^{\prime },x^{\prime \prime })|f(x^{\prime },y_j)\ge f(x^{\prime },y_j),(x^{\prime },x^{\prime \prime })\in Z_j\times {\hat{Z}}_j\}|}{|Z_j||{\hat{Z}}_j|}$$
  Z j = { x i ∣ y j ∈ Y i , 1 ≤ i ≤ p } Z_j = \{x_i|y_j \in Y_i, 1\leq i \leq p\} Zj​={xi​∣yj​∈Yi​,1≤i≤p}表示的是含有$y_j$标签的样本数量，
  Z ^ j = { x i ∣ y j ∉ Y i , 1 ≤ i ≤ p } \hat Z_j = \{x_i|y_j \notin Y_i, 1\leq i \leq p\} Z^j​={xi​∣yj​∈/Yi​,1≤i≤p}表示的是不含有$y_j$标签的样本数量

• AUC-micro(“排序正确”的数据对的占比，把多个标签考虑在内来计算占比)
  $$AU{C}_{micro}=\frac{1}{q}\sum _{j=1}^{q}AU{C}_j=\frac{1}{q}\sum _{i=1}^q\frac{|\{(x^{\prime },x^{\prime \prime },y^{\prime },y^{\prime \prime })|f(x^{\prime },y^{\prime })\ge f(x^{\prime \prime },y^{\prime \prime }),(x^{\prime },y^{\prime })\in S^{+},(x^{\prime \prime },y^{\prime \prime })\in S^{-}\}|}{|S^{+}||S^{-}|}$$
  $S^{+}=(x_i,y)|y\in Y_i,1\le i\le p$表示的是相关的样本标签对，
  $S^{-}=(x_i,y)|y\notin Y_i,1\le i\le p$表示的是不相关的样本标签对

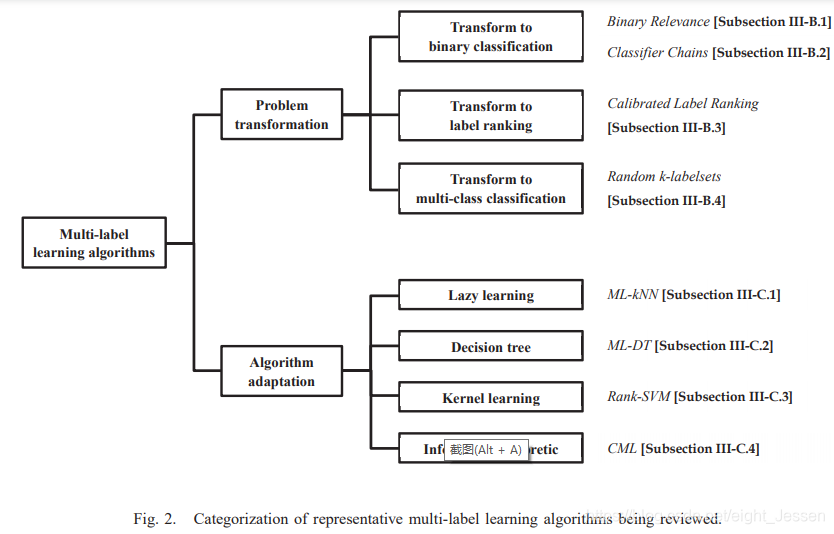
三、多分类学习算法

两种学习方法：

1. 问题转换法（让数据适应算法）
   把多标签分类转为其他成熟的场景。代表算法有一阶binary revevance和高阶方法classifier chains。他们将多标签问题转为二分类。二阶方法有calibrated label ranking。将多标签分类转为标签排序，高阶方法radom k-labelset将多标签学习转为多分类问题。
2. 算法改编方法（让算法适应数据）
   更改学习技术来应对多标签数据。代表算法包括一阶方法ML-knn改编k近邻，一阶方法ML-DT改编决策树，二阶方法Rank-SVM改编核技巧，二阶方法CML改编information-theretic techniques。