Python - 深夜数据结构与算法之 ArrayList

一.引言

二.ArrayList 介绍

1.List

2.Linked List

3.Skip List

三.经典算法实战

1.Two-Sum [1]

2.Three-Sum [15]

3.Merge-Two-Sorted-List [21]

4.Remove-Duplicates-From-Sorted-Array [26]

5.Plus-One [66]

6.Rotate-Array [189]

7. Move-Zero [283]

四.总结

一.引言

本文介绍 Python 中的 ArrayList，主要表现形式为列表和链表，其在 Python 中表示为 []。

二.ArrayList 介绍

1.List

◆ 快速访问

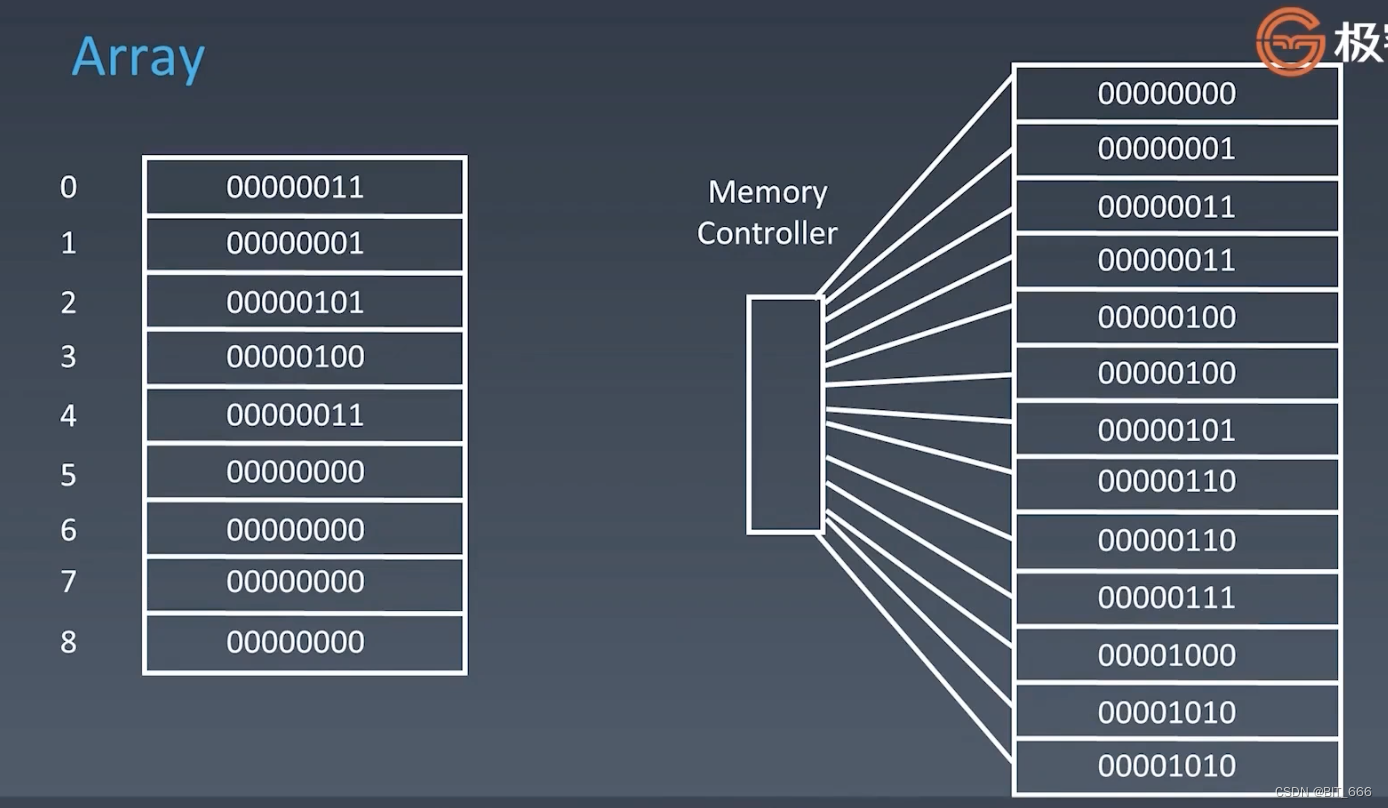
每当我们申请创建数组时，计算机会为数组开辟一段连续的地址，每个地址可以通过内存管理器即上面的 Memory Controller 直接访问到，所以访问数组中任意一个元素的时间复杂度都是一样的，即 o(1)，所以数组的访问速度非常快。

◆ 元素增删

增加元素最好的情况是从尾部 append，此时时间复杂度 o(1)，最坏情况下插入到首位，需要挪动数组内全部元素，此时时间复杂度 o(n)，平均下来需要挪动 n/2 个元素。

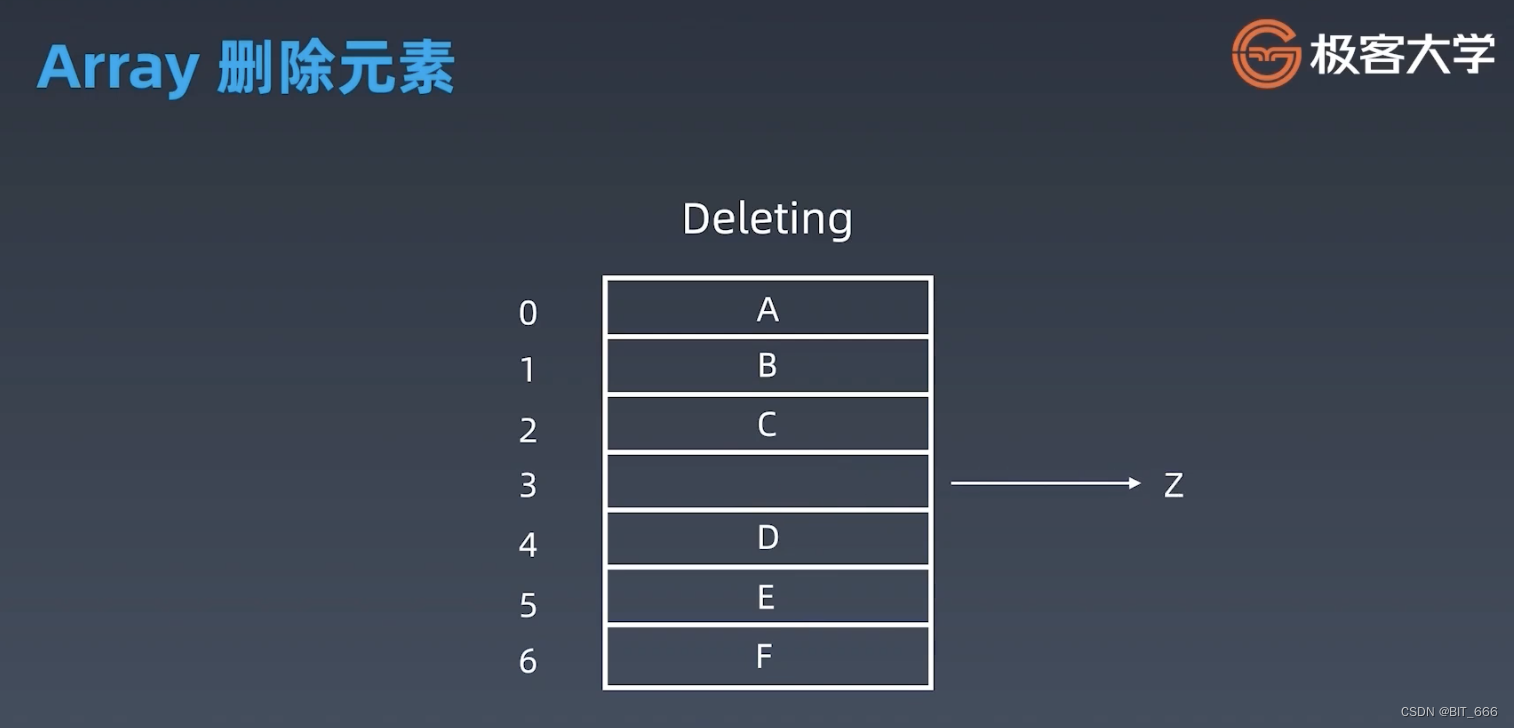
同理元素删除时也会有类似的时间复杂度，当把元素 Z 从数组中拿出去后，将 DEF 前移，此时将位置 6 置为 None，如果是 Java 会触发类似的垃圾回收机制，对空闲内存进行回收。

◆ 时间复杂度

ArrayList 具有 o(1) 的前后插入和查询的时间复杂度，但是插入和删除除首尾位置的元素，时间复杂度均为 o(n)。

2.Linked List

◆ 常见定义

# Definition for singly-linked list.
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

链表 Node 节点一般包含一个自身值 val 以及一个 next 指针指向其下一个元素，如果 next 为 None 代表没有后续的节点。

◆ 增加节点

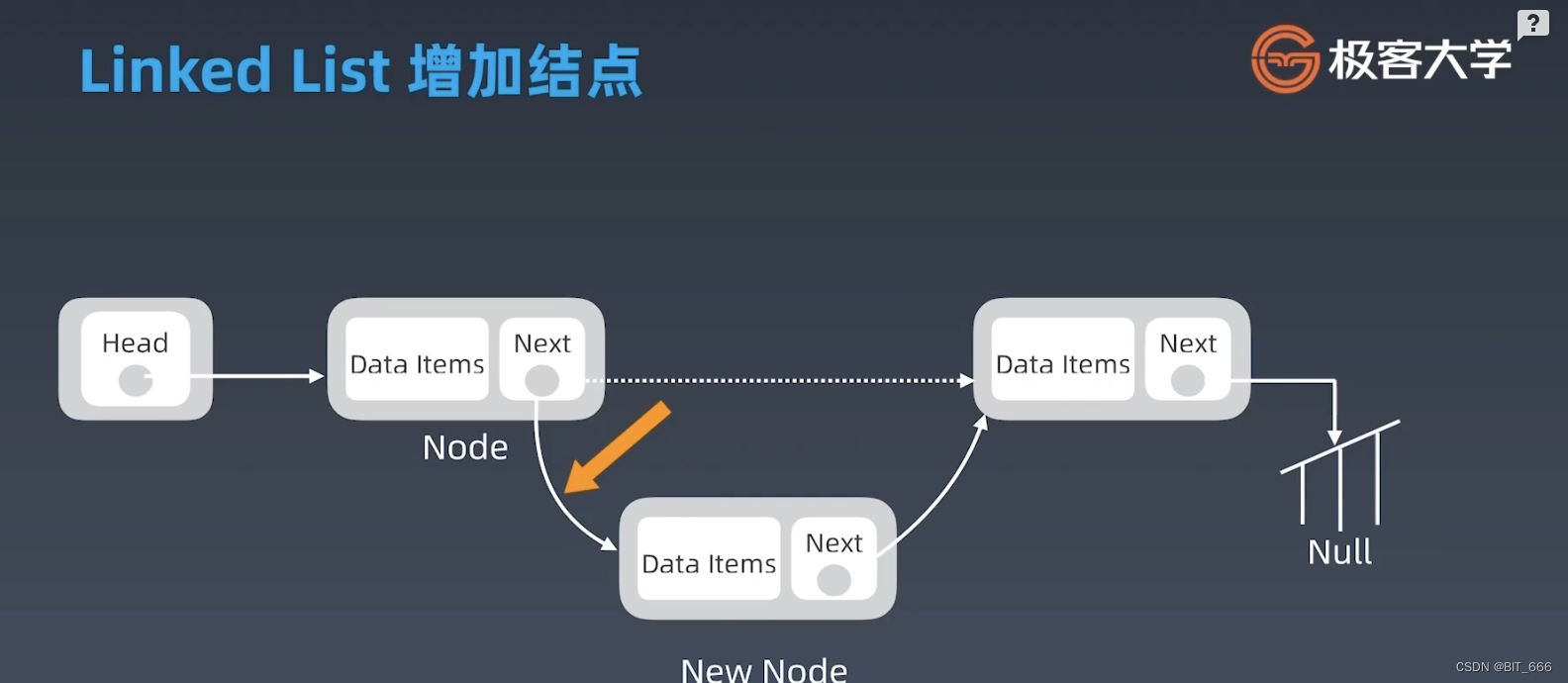
链表增加节点只需将对应位置的 Node 的 next 指向 New Node，再将 New Node 的 next 指向原先的 next 节点，进行一次转换即可，操作的时间复杂度是 o(1)。

◆ 删除节点

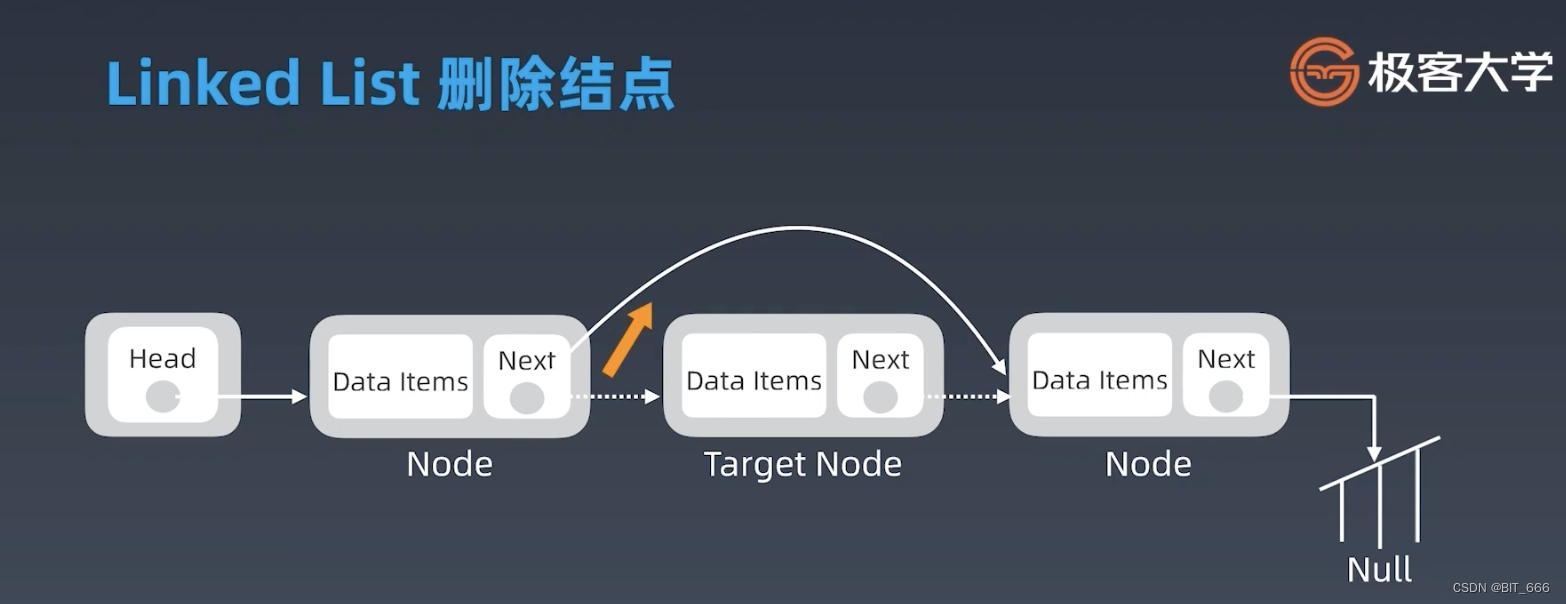
与上面添加类似，只需将待删除的 Target Node 忽略，直接将前项的 Node 节点 next 指向后项的 Node 节点即可，其时间复杂度同样为 o(1)。

◆ 时间复杂度

链表增删节点的时间复杂度均为 o(1)，但是由于其连接的结构，要想访问链表中间位置的元素，需要一个 next 一个 next 访问，所以查询元素的复杂度为 o(n)。

3.Skip List

◆ 基本性质

◆ 跳表形式

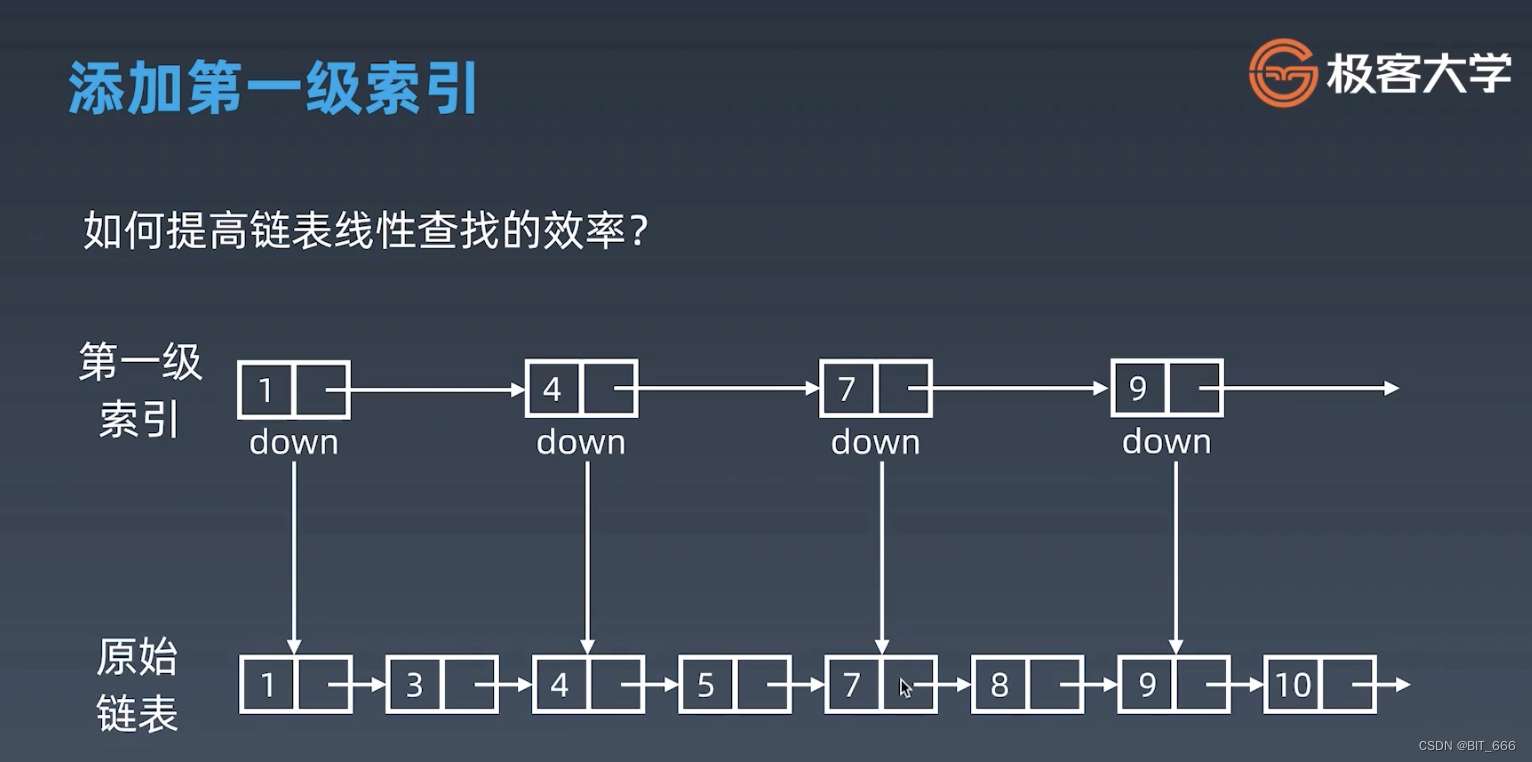
基于二分查找的思想，对于原始的元素有序的链表，我们可以添加一级索引，加速链表查询的步伐，假设我们查找 7，我们只需要在一级索引先查询，这时 1-4 本来需要 next.next 查询，而用第一级索引只需要 next 即可。随着索引层级的增多，我们查询的步伐也越来越大，其速度也越来越快，不过随之而来的是存储的增加，所以这也是一种空间换时间的经典算法思想。

◆ 时间复杂度

由于是二分查找，随着每一层索引的增加，第 k 层对应的索引节点数就为 n / (2^k)，层高 h 即为我们查找的时间复杂度，这里和前面介绍的 Trie 字典树也很像，我们只需要层高次查询即可查到对应的单词，即 o(logn)。

◆ 空间复杂度

根据每 x 个节点抽取数据的不同，我们每层的节点数目也不相同，但是由于最上面的数列是收敛的，其计算下来空间复杂度仍然为 o(n)，但是相比于前面的 List 和 Linked List，其实上面还是多了很多元素。

三.经典算法实战

上面我们介绍了 ArrayList 的几种表现形式以及其对应的一些特性，下面挑选一些 LeetCode 上比较经典的算法，加深 ArrayList 这个数据结构的印象和使用技巧。这里约定一下每个算法的表现形式，Two-Sum 代表算法名称，[x] 中括号里的 x 代表其对应 LeetCode 的第几题。

1.Two-Sum [1]

两数之和: https://leetcode.cn/problems/two-sum/description/

◆ 题目分析

最最最基础的数组算法题，学计算机没做过 Two-Sum，就像考研英语没有背 Abandon 一样。针对本题，基本有两种思路。一种是直接两层 for 循环搞定，但是相对不够优雅；还有一种是借助 HashMap，通过空间辅助。

◆ 双重循环

    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        length = len(nums)
        for i in range(length):
            for j in range(i + 1, length):
                if nums[i] + nums[j] == target:
                    return [i, j]
        return []

这里 i 遍历 range(length)，j 遍历 range(i+1，length)，其实就是枚举了数组中两两元素之间所有的可能，这里找到满足条件的 [i, j] 返回即可。时间复杂度 o(n^2)，因为遍历了两轮数组，空间复杂度 o(1)，没有使用额外的空间。

◆ HashMap 缓存

    def twoSum(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: List[int]
        """
        m = {}
        
        for i in range(0, len(nums)):
            cur = target - nums[i]
            if (cur in m):
                return [m[cur], i]
            m[nums[i]] = i
        
        return []

m 用于缓存元素及其对应索引 index，我们只需要一层循环，由于 x + y = target，所以 y = target - x，针对每一个元素 x，我们只需要找 y 在不在 m 中，如果在的话返回二者索引即可，如果不在，则将当前元素缓存至 m 中。这里时间复杂度 o(n) 因为只 for 循环遍历了一次数组，空间复杂度也是 o(n)，因为最差需要存储 n-1 个元素。

2.Three-Sum [15]

三数之和: https://leetcode.cn/problems/3sum/description/

◆ 题目分析

两数之和、三数之和都是非常经典的算法题目，这里题目要求 i、j、k 三处的元素相加为 0。我们可以进行转换， nums[i] + nums[j] = -1 * nums[k]，再令 -1 * nums[k] 为 Target，即可将题目转换为 Two-Sum，唯一区别是我们需要遍历多个 k 生成多个 Target，相当于做多次 Two-Sum。审题后我们大致得到下述信息：结果为不重复的三元组、a + b + c = 0 => a + b = -c。

◆ 双指针

def threeSum(nums):
    result = []
    # 先将 nums 排序
    nums.sort()

    for k in range(len(nums) - 2):
        # 位置 k>0，则 k 后面的加起来必不可能为 0
        if nums[k] > 0:
            break

        # 排除两数相同的情况
        if k > 0 and nums[k] == nums[k - 1]:
            continue

        i, j = k + 1, len(nums) - 1

        while i < j:
            total = nums[i] + nums[j] + nums[k]

            if total < 0:
                i += 1
            elif total > 0:
                j -= 1
            else:
                # 排除左边、右边重复的情况
                result.append([nums[i], nums[j], nums[k]])
                while i < j and nums[i] == nums[i + 1]:
                    i += 1
                while i < j and nums[j] == nums[j - 1]:
                    j -= 1
                i += 1
                j -= 1
    return result

下面我们看下双指针的实现思路:

nums.sort() - 将数组排序后可以根据和的大小对左右指针进行移动

range(len(nums) - 2) - 因为是三元组，所以只需要遍历到倒数第 3 个元素即可

nums[k] > 0 - 因为数组有序，如果 k > 0，则 k 后面的三个元素怎么相加都可能为 0

nums[k] == nums[k-1] - target = nums[k] * 1，这里 continue 相当于实现了基于 target 的去重

while i < j - 左右指针进行夹逼法，如果满足 total = 0，则将 [i, j, k] 添加到 result 中

nums[i] == nums[i+1] - 这里相当于实现了基于三元组元素的去重

i += 1, j -= 1 - 完成一组解答后，继续遍历其他的 i，j 的情况

Tips:

这里双指针的用法是 ArrayList 非常经典的算法，很多题目都可以借助双指针的思想，一定要好好掌握。

3.Merge-Two-Sorted-List [21]

合并两个有序链表: https://leetcode.cn/problems/merge-tow-sorted-lists/

◆ 题目分析

L1、L2 为给定的两个有序链表，需要将两个有序链表合成一个新的有序链表，思路比较好想但是实现起来需要一点技巧。这里需要构建一个新的 Node 节点，分别比较 L1 和 L2 的 head，将较小的节点连接到 Node，即 Node.next = Smaller，随后把 L1 或 L2 指向 next ，直到其中某个为空，再将剩下的节点补齐至最后即可。

◆ 递归实现

    def mergeTwoLists(self, list1, list2):
        if not list1: return list2
        if not list2: return list1

        if list1.val <= list2.val:
            list1.next = self.mergeTwoLists(list1.next, list2)
            return list1
        else:
            list2.next = self.mergeTwoLists(list1, list2.next)
            return list2

这里开始的 not list1 和 not list2 用于检测链表为空的情况。后面判断大小也很好理解，博主当时有疑问的地方是 return list1，list2 这个部分，后来看了乐扣上网友的分析感觉很有道理:

递归的核心在于，我只关注我这一层要干什么，返回什么，至于我的下一层(规模减1)，我不管，我就是甩手掌柜.

自己的理解:

结合这个图，针对最前面的 list，其只管返回自己即可，后面其余部分的链表合并可以看做是一个整体，和他没有关系，他甩手后面自己合并即可，但是他需要返回，因为这里不返回的话我们最终就没有最终输出结果了。

◆ 从头再来

    def mergeTwoLists(self, l1, l2):
        cur = dummy = ListNode() # dummy 为影子节点

        while l1 and l2:
            # 判断数值并更新链表
            if l1.val > l2.val:
                cur.next = l2
                l2 = l2.next
            else:
                cur.next = l1
                l1 = l1.next

            cur = cur.next
        
        # 补齐剩下的有序链表   
        if l1:
            cur.next = l1
        if l2:
            cur.next = l2

        return dummy.next

这一版实现和我上面自己的思路分析比较一致，因为递归的思想有时候并不是很好想或者实现。这里 dummy 又称为影子节点，因为 cur 需要随着 while 循环逐步推进，这时候 cur 和 dummy 都指向同一个地址，我们后续想要获得头结点就只需要 dummy.next 即可，其主要是这个作用。whlie 和下面 if 的比较好理解，这一版是自己的思路实现，感觉更符合自己目前的水平哈哈。

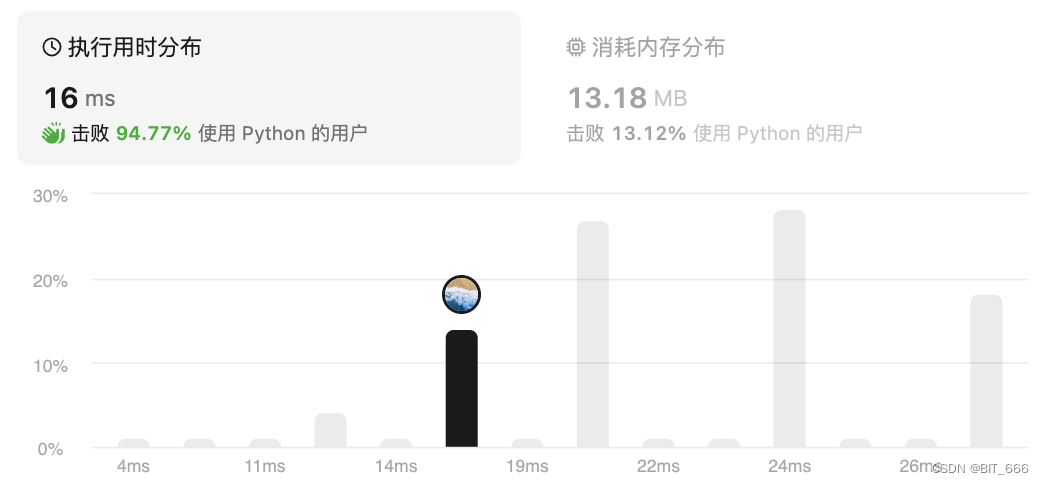
4.Remove-Duplicates-From-Sorted-Array [26]

有序数组移除重复元素: https://leetcode.cn/problems/remove-duplicates-from-sorted-array

◆ 题目分析

数组是非严格递增的，代表可能存在相同的元素。原地删除元素，代表我们不能引入额外的数据结构处理，例如引入 set 直接去重。最后是返回值，这里返回 nums 中非重复元素的数组长度而不是非重复元素。

◆ 单指针

    def removeDuplicates(self, nums):

        # 长度为 1 直接返回
        if len(nums) == 1:
            return 1

        j = 0
        # 判重
        for i in range(len(nums)):
            if nums[i] != nums[j]:
                j += 1
                nums[j] = nums[i]

        return j + 1

引入单指针索引 j，遍历每个元素，如果其与上一个 j 对应的元素不相等，则 j += 1，放置新的非重复元素，最后由于数组索引是 0 开始，所以我们返回长度需要返回 j + 1。

5.Plus-One [66]

数组元素加一: https://leetcode.cn/problems/plus-one/description/

◆ 题目分析

这一题使用数组表示数字，将数字 +1 后再重新使用数组表示，数学逻辑的话很简单，就是一个加法，主要是其涉及到进位所以对于数组长度以及数组的索引元素会造成修改，所以我们主要进位导致的这两个问题即可。自己想了两个思路，一种是把数字 Int 直接提出来，加完再找新数组放进去；另外就是原地执行，通过一个辅助变量记录是否进位。

◆ 直截了当

    def plusOne(self, digits):
        """
        :type digits: List[int]
        :rtype: List[int]
        """
        
        num = ""
        for i in digits:
            num += str(i)

        plus = str(int(num) + 1) # 数组转数字 Int

        re = []
        for i in plus:
            re.append(int(i))

        return re

这个方法是我读题第一时间想到的，执行起来看着还能接受，内存也没有消耗过大。

◆ 原地起飞

    def plusOne(self, digits):

        length = len(digits)
        is_add = False # 记录是否进位
        for i in range(length):
            # 因为加法从个位开始，所以数组从后向前遍历
            cur_index = length - (i + 1)
            cur_value = digits[cur_index]

            if is_add or i == 0:
                cur_value = cur_value + 1
            
            # 判断是否需要进位    
            if cur_value >= 10:
                is_add = True
                digits[cur_index] = 0
            else:
                is_add = False
                digits[cur_index] = cur_value

        # 判断是否需要在数组前追加一位
        if is_add:
            return [1] + digits
        else:
            return digits

这个就是正常的加法逻辑，其通过 is_add 记录是否需要进位，随后从后向前没遍历一位都执行相加和修改元素，最后再判断一次 is_add 判断相加是否导致数字进位从而为数组补一位。由于是原地执行，所以内存的占用会比上面的方法小一些。

6.Rotate-Array [189]

轮转数组: https://leetcode.cn/problems/rotate-array/description/

◆ 题目分析

根据 k 的步伐，数组后面的元素依次挤过来，前面的被顶到后边。以 [1,2,3,4,5,6,7] k=3 为例，挪动后的数组为 [5,6,7,1,2,3,4]，所以 k 次移动对应的是 -k 即倒数 k 的元素对应的数组挪到前面，再把剩下的数组挪到后面。

◆ 前后颠倒 - 错误版

    def rotate(self, nums, k):
        """
        Do not return anything, modify nums in-place instead.
        """
        if k == 0:
            return nums
        else:
            length = len(nums)
            move = k % length

            return nums[-move:] + nums[:-move]

这一版按照我们前面的思路写的，k % length 是为了防止数组轮转多遍。但是执行后会报错:

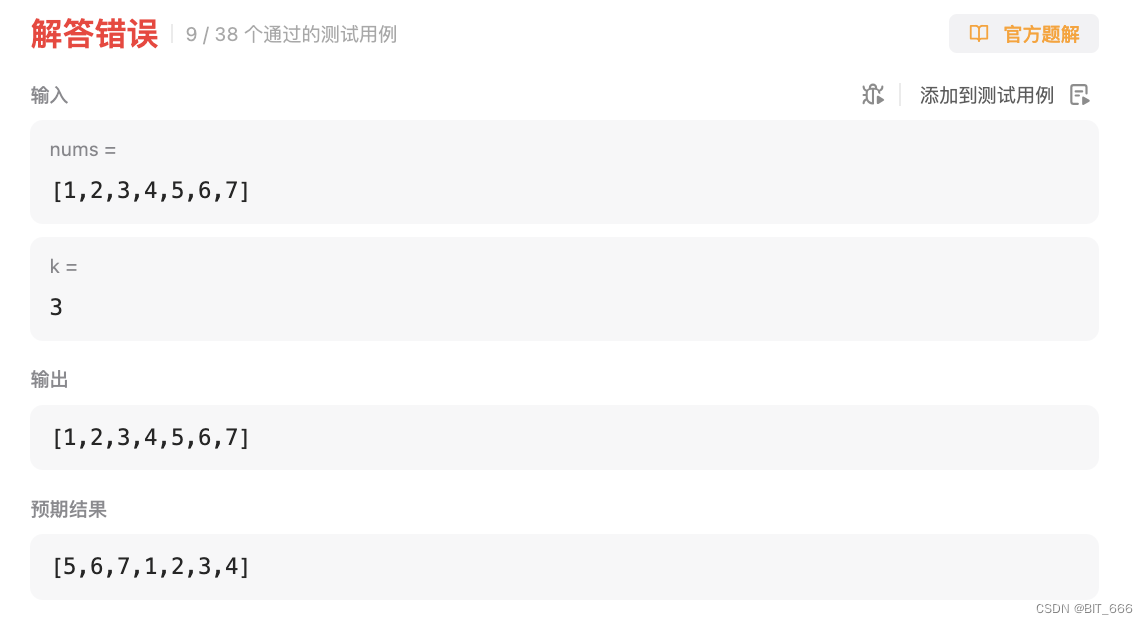
都是 "Do not return anything, modify nums in-place instead" 惹的祸，还是读题不严谨，而且题目要求原地修改，不允许修改内存地址。

◆ 前后颠倒 - 正确版

    def rotate(self, nums, k):
        """
        Do not return anything, modify nums in-place instead.
        """
        if k == 0:
            return nums
        else:
            length = len(nums)
            move = k % length

            nums[:] = nums[-move:] + nums[:-move]

这里去掉了 return，增加了 nums[:]，[:] 的写法可以保持内存地址 id 不变，而 '=' 号后面的写法负责改变 value，这样就实现了数组轮转。

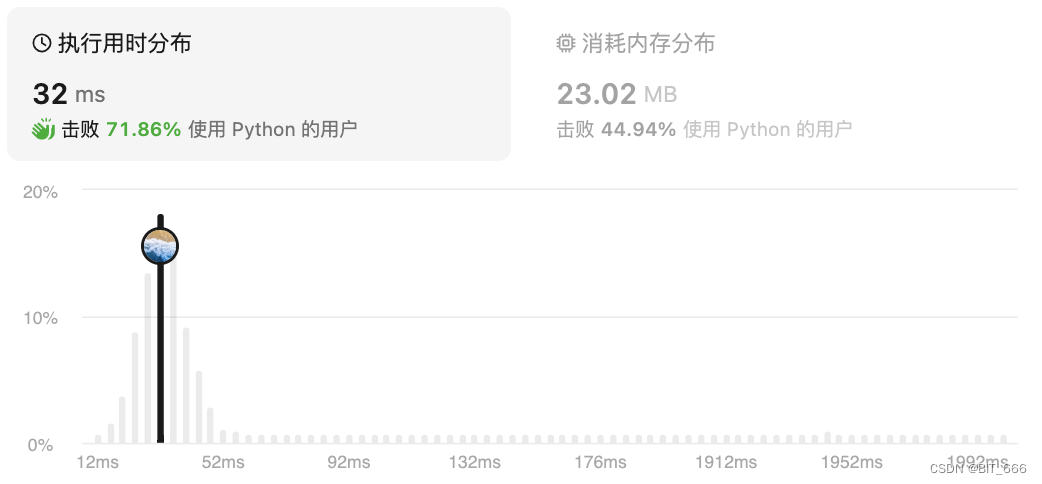
◆ 旋转跳跃

class Solution:

    # 数组对称交换
    def swap(self, nums, left, right):
        while left < right:
            nums[left], nums[right] = nums[right], nums[left]
            left += 1
            right -= 1
        
    # 换就完事了
    def rotate(self, nums, k):
        """
        Do not return anything, modify nums in-place instead.
        """
        if k == 0:
            return nums
        else:
            length = len(nums)
            k %= length
            self.swap(nums, 0, length-k-1)
            self.swap(nums, length-k, length-1)
            self.swap(nums, 0, length-1)

除了上面精简的写法外，还有一个 swap 的方法，其是根据元素对称性实现的，为了更好的理解代码，下面给出简单的执行过程，还是以 [1,2,3,4,5,6,7] k=3 为例：

第一次 swap: [4,3,2,1,7,6,5] 反转前面 n-k 个

第二次 swap: [1,2,3,4,7,6,5] 反转后 k 个

第三次 swap: [5,6,7,1,2,3,4] 整体前后反转

多次 swap 执行时间较长，但是由于 swap 是原地交换，所以内存消耗较小。

7. Move-Zero [283]

移动零: https://leetcode.cn/problems/move-zeroes/description/

◆ 题目分析

将所有零移动到数组后面，且不改变原始顺序，还是前面的思路方法，我们引入一个单指针，记录存放非0元素的位置，遇到为零的元素 i，将该元素与 j 交换，相当于把 0 扔后面，把非 0 拿到前面，再将 j += 1 指定下一个存放非 0 位置的元素即可。

◆ 斗转星移

class Solution(object):

    def swap(self, i, j, nums):
        nums[i], nums[j] = nums[j], nums[i]


    def moveZeroes(self, nums):
        """
        Do not return anything, modify nums in-place instead.
        """
        j = 0
        for i in range(len(nums)):
            if nums[i] != 0:
                self.swap(i, j, nums)
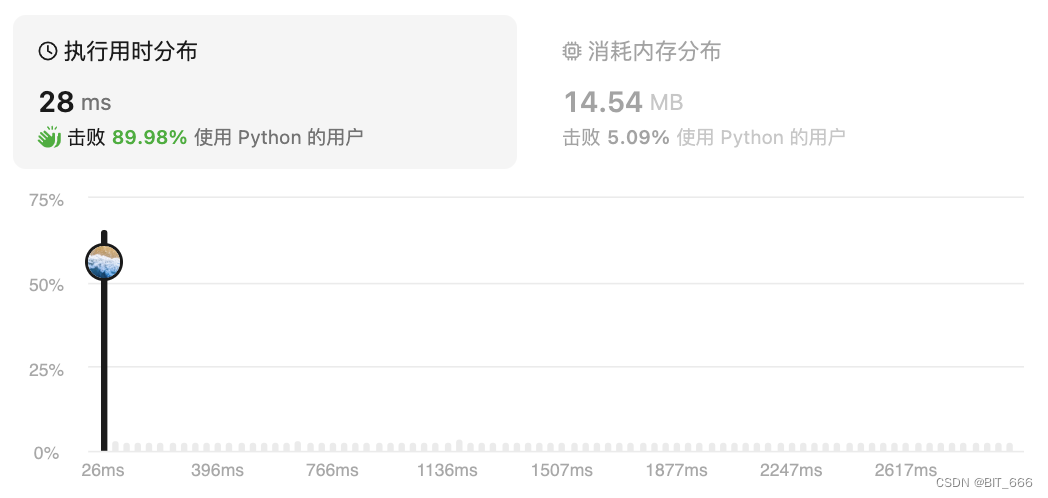
                j += 1

前面是数组的 swap，这个是直接 i、j 索引的 swap，遍历数组，判断非零元素并交换即可。以 [0,1,0,3,12] 为例:

i=1, j=0 => [1,0,0,3,12]

i=3, j=1 => [1,3,0,0,12]

i=4, j=2 => [1,3,12,0,0]

四.总结

上面讲解了数组的基本概念以及 LeetCode 里一些基本的算法操作，这里介绍的题目以简单和中等为主，主要是用于了解一些常用的算法实现方式，这里数组和链表我们使用了：单指针、双指针、递归、元素 swap、数组 swap、空间换时间等最常用的技巧，后面可以多多练习加深印象，博主也会出其他数据结构的相关栏目。

本文都是工作之外的时间创作，大部分在晚上，所以其名为 <深夜数据结构与算法>，整理一篇文章大概需要两周左右，创作不易，如果对你有帮助，欢迎留下痕迹 ^_^