import numpy as np
import matplotlib.pyplot as plt

f = lambda x: (x - 3.5) ** 2 - 4.5 * x + 10
x = np.linspace(0, 10, 200)
y = f(x)
plt.plot(x, y, color='g')

方式一： 求导

g = lambda x: 2 * (x - 3.5) - 4.5
# 令导数等于0  g=0
# 0 = 2 * (x-3.5)-4.5
# 2x - 11.5 = 0
x_min = 11.5 / 2
print(x_min)

方式二：梯度下降

if np.abs(x_ - last_x_) < precision: 通过对x_和last_x_进行对比查看学习率的变化判断是不是已经达到了最优

step = 0.01  #学习率
# 瞎蒙  随机的最小值
x_ = np.random.randint(0, 12, size=1)[0]
print("随机生产学习", '+++++++++++++++++++++++++++++++', x_)
# 记录上一次梯度下降的x_值
last_x_ = x_ + 2  # 只要与x_有一个比较大差值，就可以
# 需要使用x_和last_x_ 差值，作为退出条件
# 精确度  退出条件
precision = 1e-4
x_result = [x_]
count = 0
while True:
    if np.abs(x_ - last_x_) < precision:
        break
    else:
        # 更新之前的last_x_
        last_x_ = x_  # 将当前的x_复制给last_x_
        # 更新当前的x_
        x_ = x_ - step * g(x_)  #梯度下降更新权重，目标值
        x_result.append(x_)
        print('__________________________________', x_)
plt.figure(figsize=(9, 6))
plt.plot(x, y, color='red')
plt.scatter(np.array(x_result), f(np.array(x_result)), color='green')

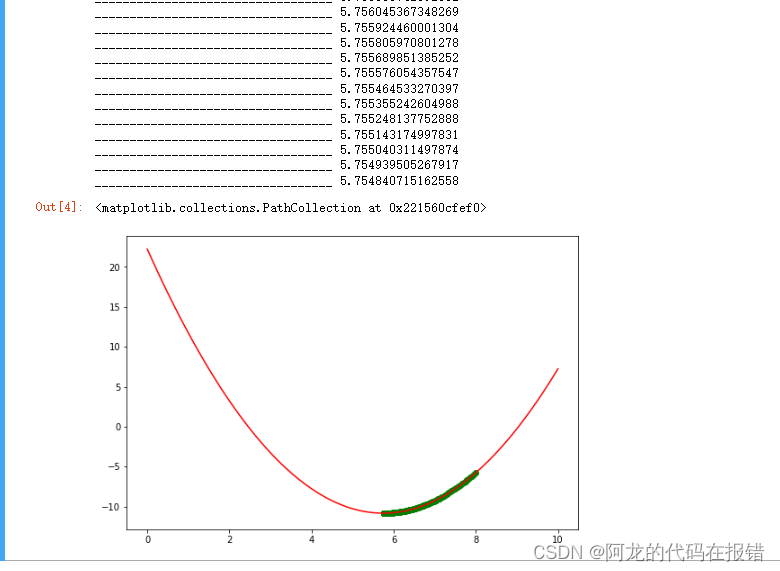
if np.abs(g(x_)) < precision: 通过公式判断导数是不是趋于0 进行判断是不是达到最优

step = 0.01  #学习率
# 瞎蒙  随机的最小值
x_ = np.random.randint(0, 12, size=1)[0]
print("随机生产学习", '+++++++++++++++++++++++++++++++', x_)
# 记录上一次梯度下降的x_值
last_x_ = x_ + 2  # 只要与x_有一个比较大差值，就可以
# 需要使用x_和last_x_ 差值，作为退出条件
# 精确度  退出条件
precision = 1e-4
x_result = [x_]
count = 0
while True:
    if np.abs(g(x_)) < precision:  # 判断的梯度趋于0，到达最小值，山谷处，她的导数为0
        break
    else:
        # 更新之前的last_x_
        last_x_ = x_  # 将当前的x_复制给last_x_
        # 更新当前的x_
        x_ = x_ - step * g(x_)  #梯度下降更新权重，目标值
        x_result.append(x_)
        print('__________________________________', x_)
plt.figure(figsize=(9, 6))
plt.plot(x, y, color='red')
plt.scatter(np.array(x_result), f(np.array(x_result)), color='green')

if np.abs((f(x_)) - f(last_x_)) / np.abs(f(last_x_)) < precision: # 利用损失函数进行判断是不是已经达到了最优

step = 0.01  #学习率
# 瞎蒙  随机的最小值
x_ = np.random.randint(0, 12, size=1)[0]
print("随机生产学习", '+++++++++++++++++++++++++++++++', x_)
# 记录上一次梯度下降的x_值
last_x_ = x_ + 2  # 只要与x_有一个比较大差值，就可以
# 需要使用x_和last_x_ 差值，作为退出条件
# 精确度  退出条件
precision = 1e-4
x_result = [x_]
count = 0
while True:
 if np.abs((f(x_)) - f(last_x_)) / np.abs(f(last_x_)) < precision:  # 利用损失函数进行判断
        break
    else:
        # 更新之前的last_x_
        last_x_ = x_  # 将当前的x_复制给last_x_
        # 更新当前的x_
        x_ = x_ - step * g(x_)  #梯度下降更新权重，目标值
        x_result.append(x_)
        print('__________________________________', x_)
plt.figure(figsize=(9, 6))
plt.plot(x, y, color='red')
plt.scatter(np.array(x_result), f(np.array(x_result)), color='green')