问题描述
八皇后问题是十九世纪著名的数学家高斯于1850年提出的。
问题是:在8×8的棋盘上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上。可以把八皇后问题扩展到n皇后问题,即在n×n的棋盘上摆放n个皇后,使任意两个皇后都不能处于同一行、同一列或同一斜线上。
显然,棋盘的每一行上可以而且必须摆放一个皇后,所以,n皇后问题的可能解用一个n元向量X=(x1, x2, …, xn)表示,其中,1≤i≤n并且1≤xi≤n,即第i个皇后放在第i行第xi列上。
由于两个皇后不能位于同一列上,所以,解向量X必须满足约束条件:
xi≠xj (式8.1)
若两个皇后摆放的位置分别是(i, xi)和(j, xj),在棋盘上斜率为-1的斜线上,满足条件i-j= xi-xj,在棋盘上斜率为1的斜线上,满足条件i+j= xi+xj,综合两种情况,由于两个皇后不能位于同一斜线上,所以,解向量X必须满足约束条件:
|i-xi|≠|j-xj| (式8.2)
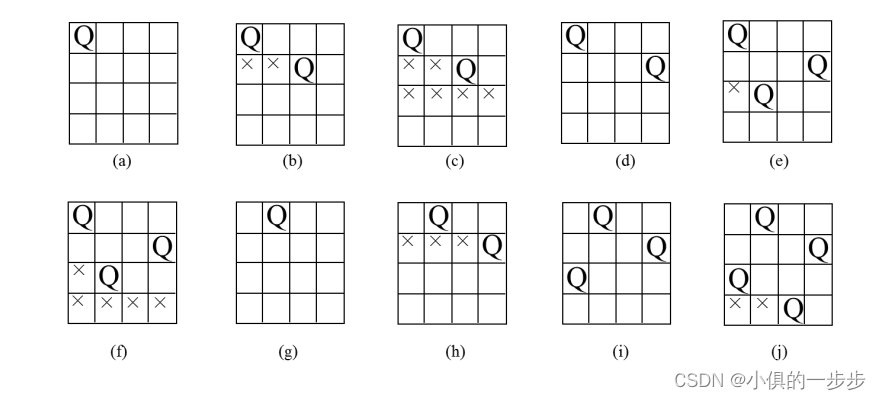
四皇后问题示例
实验目的
(1)掌握回溯算法的设计思想;
(2)掌握解空间树的动态生成过程。
实验要求
(1)设计解空间树的动态生成算法,并设计剪枝函数加快搜索速度;
(2)将上面图例(四皇后问题)按回溯算法搜索并输出全部的解。
核心思路:
使用递归+回溯
1.初始化棋盘全部为“.”
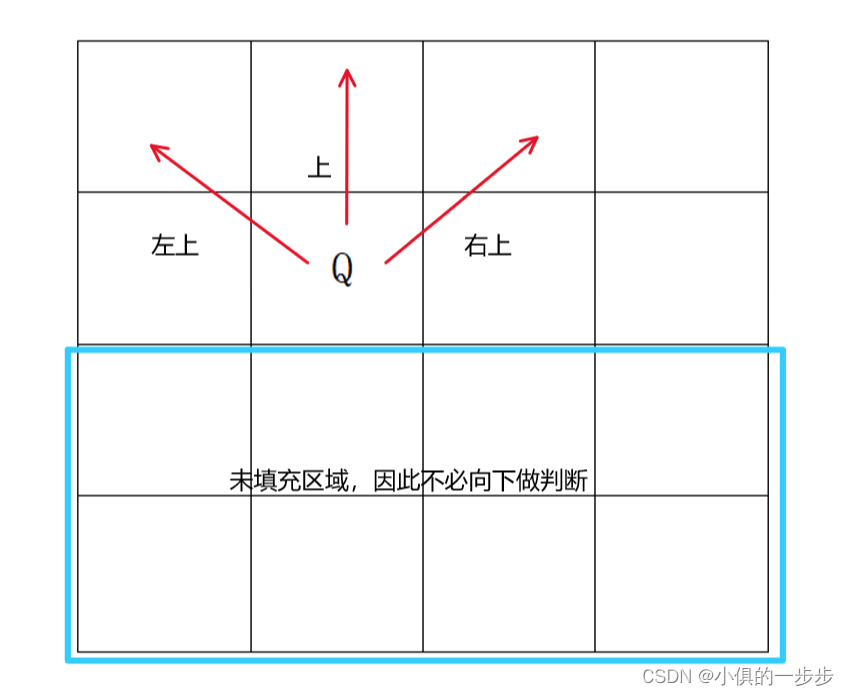
2.从第一行开始,遍历该行的每一个位置,符合的填为“Q”,不符合的跳过,再递归下一行,遍历完下一行后,将该行当前位置又重置为“.”,这一过程就是回溯的过程。依次 遍历进行判断每一行。
判断位置是否可以放“Q”:
算法实现:
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
public class S51 {
List<List<String>> res = new LinkedList<>();
public List<List<String>> solveNQueens(int n) {
char[][] borad = new char[n][n];
//初始化棋盘
for (int i = 0; i < borad.length; i++) {
Arrays.fill(borad[i], '.');
}
backtrack(0, borad);
return res;
}
/**
* 第row行的填充结果
* @param row 到第row行
* @param borad 棋盘
*/
private void backtrack(int row, char[][] borad) {
if (row < 0 || row > borad.length) {
return;
}
if (row == borad.length) {
List<String> item = new LinkedList<>();
for (int i = 0; i < borad.length; i++) {
StringBuffer sb = new StringBuffer();
for (int j = 0; j < borad[0].length; j++) {
//方便打印结果一目了然添加“\t”
sb.append(borad[i][j]+"\t");//改为sb.append(borad[i][j]),即可解决力扣51题
}
item.add(sb.toString());
}
res.add(item);
return;
}
int n = borad[row].length;
//对row行的每个位置进行判断是否符合放皇后的位置
for (int col = 0; col < n; col++) {
if (!isfang(row, col, borad)) {//已放过,即不符合
continue;
}
borad[row][col] = 'Q';
//进入下层决策
backtrack(row + 1, borad);
//回溯
borad[row][col] = '.';
}
}
/**
* 判断【row,col】位置是否可以放皇后
* @param row 行
* @param col 列
* @param borad 棋盘
* @return true 可放
*/
private boolean isfang(int row, int col, char[][] borad) {
int n = borad.length;
//竖直上方
for (int k = 0; k <= row; k++) {
if (borad[k][col] == 'Q') {
return false;
}
}
//右上方
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (borad[i][j] == 'Q') {
return false;
}
}
//左上方
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (borad[i][j] == 'Q') {
return false;
}
}
return true;
}
public static void main(String[] args) {
S51 s51 = new S51();
int n = 4;
List<List<String>> lists = s51.solveNQueens(n);
System.out.println(n+" 皇后的解法如下:");
for (int i = 0; i < lists.size(); i++) {
List<String> res = lists.get(i);
System.out.println("结果"+(i+1)+":");
for (int j = 0; j < res.size(); j++) {
System.out.println(res.get(j));
}
System.out.println();
}
}
}
输出结果:
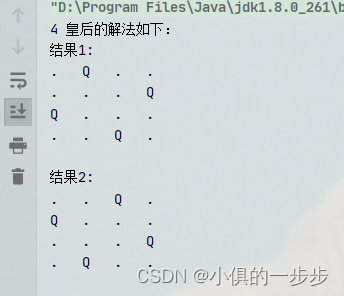
将以上代码中‘sb.append(borad[i][j]+"\t")’改为sb.append(borad[i][j]),就可以提交通过力扣51题
51. N 皇后

快去提交吧~~~