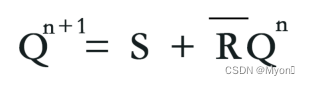思路来源

https://www.tuicool.com/articles/ee2QZf6

spoj375(树链剖分)-CSDN博客

概念

直接扒过来了，懒得写了……

显然轻子树比重子树小，就少于父亲的一半，

然后性质2的证明就是基于此的……

因为重链是间断的，所以两条重链夹着一条轻边，

然后若重链x条，必夹着(x-1)条轻边，由x-1为log级则重链log级

心得

及时把板子总结好到时候就能改吧改吧应对各种情况……

dfs1就是树形dp的基础操作，把要处理的都处理好

par[]:当前点的父亲
dep[]:当前点的深度(以根为0) 
siz[]:当前点的子树大小(包括自己)
son[]:当前点的重儿子(siz最大的那个儿子)
id[]:dfs序时间戳 
arc[]:id[]的映射,如id[u]=v,则arc[v]=u 
top[]:某一条链最靠近树根的结点 即边最靠上的那个端点 
tree[]:按照dfs序建的线段树 重链映射到连续区间 轻链映射到一个点 
cnt:edge的标号;num:时间戳的标号

dfs2的时候处理dfs序，优先搜索重儿子，这样重儿子就会堆到一起形成一个连续的区间

然后剩下的就是处理dfs序的线性序列，线段树操作，很常见的

询问u到v的时候，每次点向该链的top上走，直到两条链的top相同，即两个点走到一条链上，最后特殊处理这条链

其实询问LCA、最大、求和的操作也都是基于此，由于链的条数是log，

对重链求和的操作是log，对轻边求和的操作是1，所以每次查询是O(logn*logn)的

嗯这么总结过了以后应该不会再忘了叭

经典的操作：

①询问u到v这条链上的最大值最小值

②询问u到v这条链上的权值之和

③询问u到v这条链上的第k大值（树剖+主席树）

儿子以父节点为pre来建树，这样每个儿子对应的树就是到根节点的这条链，

询问u->v这条链内的权值的时候，u+v-lca(u,v)-par[lca(u,v)]，传参查kth的时候传进去四棵树的参数就可以了

画一下图就搞出来了，lca(u,v)到根都被记了两遍，剩下的部分都被记了一遍

而lca(u,v)是需要一遍的，剩下的par[lca(u,v)]是需要被记零遍的，对应减掉就可以了

例题

bzoj2588 Spoj 10628. Count on a tree（主席树+树剖）

题解【主席树】bzoj2588 Spoj 10628. Count on a tree - AutSky_JadeK - 博客园

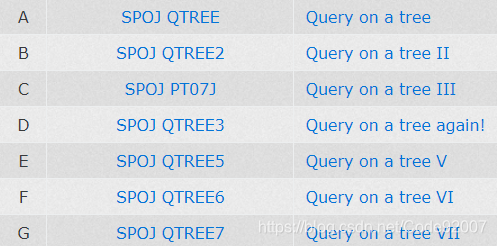
代码1（根据点权dfs序建树）

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn=1e5+10;
typedef long long ll;
struct edge
{
	int to,nex,w;
}e[maxn*2];  
struct node
{
	int max;
	ll sum;
}tree[maxn*5];
//par[]:当前点的父亲
//dep[]:当前点的深度(以根为0) 
//siz[]:当前点的子树大小(包括自己)
//son[]:当前点的重儿子(siz最大的那个儿子)
//id[]:dfs序时间戳 
//arc[]:id[]的映射,如id[u]=v,则arc[v]=u 
//top[]:某一条链最靠近树根的结点 即边最靠上的那个端点 
//tree[]:按照dfs序建的线段树 重链映射到连续区间 轻链映射到一个点 
//cnt:edge的标号;num:时间戳的标号
int par[maxn],dep[maxn],siz[maxn],son[maxn],top[maxn];
int head[maxn],cnt,a[maxn];
int id[maxn],arc[maxn],num;
int n,q;
char op[10];
void add(int u,int v,int w)
{
	e[cnt].to=v;
	e[cnt].w=w;
	e[cnt].nex=head[u];
	head[u]=cnt++;
}
void init()
{
	//memset(par,0,sizeof(par)); 由于dfs1的时候会覆盖 不需要 
	//memset(dep,0,sizeof(dep)); 由于后续dep[v]=dep[u]+1 只需更新根节点 
	//memset(siz,0,sizeof(siz)) 由于siz[u]=1覆盖 不需要 
	//memset(tree,0,sizeof(tree));
	//memset(top,0,sizeof(top)); 后续都是根据根节点更新的 
	//memset(id,0,sizeof(id)); num=0了什么都好说 
	dep[1]=0;top[1]=1;
	memset(son,0,sizeof(son));
	memset(head,-1,sizeof(head));
	cnt=num=0; 
	
}
void dfs1(int u)
{
	siz[u]=1;
	for(int i=head[u];~i;i=e[i].nex)
	{
		int v=e[i].to;
		if(v!=par[u])
		{
			par[v]=u;
			dep[v]=dep[u]+1;
			dfs1(v);
			siz[u]+=siz[v];
			if(siz[v]>siz[son[u]])son[u]=v;
		}
	}
}
void dfs2(int u)
{
	id[u]=++num;//dfs序 时间戳 id[i]即在线段树的第i位 想象给一颗dfs树标号 
	arc[id[u]]=u;//arc[i] 第i位的值对应的原节点 
	if(son[u])//优先遍历重儿子 保证重链dfs序相邻 
	{
		top[son[u]]=top[u];//重链上的根一定和父相同
		dfs2(son[u]); 
	} 
	for(int i=head[u];~i;i=e[i].nex)
	{
		int v=e[i].to;
		if(v!=par[u]&&v!=son[u])//非父 轻儿子
		{
			top[v]=v;//轻链以自己为根
			dfs2(v); 
		} 
	}
}
void pushup(int p)
{
	tree[p].sum=tree[p<<1].sum+tree[p<<1|1].sum;
	tree[p].max=max(tree[p<<1].max,tree[p<<1|1].max);
} 
void build(int p,int l,int r)
{
	if(l==r)
	{
		tree[p].sum=tree[p].max=a[arc[l]];
		return;
	}
	int mid=(l+r)>>1;
	build(p<<1,l,mid);
	build(p<<1|1,mid+1,r);
	pushup(p);
} 
void update(int p,int l,int r,int pos,int v)//单点修改 
{
	if(l==r)
	{
		tree[p].sum+=v;
		tree[p].max+=v;
		return; 
	}
	int mid=(l+r)>>1;
	if(pos<=mid)update(p<<1,l,mid,pos,v);
	else update(p<<1|1,mid+1,r,pos,v);
	pushup(p);
}
ll asksum(int p,int l,int r,int ql,int qr)//区间和 
{
     if(ql<=l&&r<=qr)return tree[p].sum;
	 ll res=0;
	 int mid=(l+r)>>1;
	 if(ql<=mid)res+=asksum(p<<1,l,mid,ql,qr);
	 if(qr>mid)res+=asksum(p<<1|1,mid+1,r,ql,qr);
	 return res;
}
ll askmax(int p,int l,int r,int ql,int qr)//区间最值 
{
	 if(ql<=l&&r<=qr)return tree[p].max;
	 ll res=-1e18;
	 int mid=(l+r)>>1;
	 if(ql<=mid)res=max(res,askmax(p<<1,l,mid,ql,qr));
	 if(qr>mid)res=max(res,askmax(p<<1|1,mid+1,r,ql,qr));
	 return res;
}
int lca(int u,int v)//重链log 轻链log 故O(log)在线查询LCA 
{
	//保证u的那条链的top一直在下 
	while(top[u]!=top[v])
	{
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		u=par[top[u]];//从top走向它的父亲 
	}
	//此时top[u]==top[v] 初始状况或未swap 判一下 返回靠上的 
	if(dep[u]>dep[v])swap(u,v); 
	return u; 
}
ll findsum(int u,int v)//u->v链之和 按轻重链找 
{
	ll ans=0;
	while(top[u]!=top[v])
	{
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		ans+=asksum(1,1,n,id[top[u]],id[u]);//重链区间和或轻链单点和 
		u=par[top[u]]; 
	}
	//u、v现在top相同 在一条链上 
	if(dep[u]>dep[v])ans+=asksum(1,1,n,id[v],id[u]);
	else ans+=asksum(1,1,n,id[u],id[v]);
	return ans; 
} 
ll findmax(int u,int v)//u->v链上的最大值 按轻重链找 
{
	ll ans=-1e18;
	while(top[u]!=top[v])
	{
		if(dep[top[u]]<dep[top[v]])swap(u,v);
		ans=max(ans,askmax(1,1,n,id[top[u]],id[u]));//重链区间和或轻链单点和 
		u=par[top[u]]; 
	}
	//u、v现在top相同 在一条链上 
	if(dep[u]>dep[v])ans=max(ans,asksum(1,1,n,id[v],id[u]));
	else ans=max(ans,asksum(1,1,n,id[u],id[v]));
	return ans; 
} 
int main() 
{
	//freopen("test.in","r",stdin);
	//freopen("test.out","w",stdout); 
	int T;
	scanf("%d",&T);
	while(T--)
	{ 
	 scanf("%d",&n);
	 init();
	 for(int i=1;i<n;++i)//树 n-1条边 边权
	 {
	 	int u,v,w;
	 	scanf("%d%d%d",&u,&v,&w);
	 	add(u,v,w);
	 	add(v,u,w);
	 }
	 for(int i=1;i<=n;++i)
	 scanf("%d",&a[i]);//点上有点权的情况 
	 dfs1(1);
	 dfs2(1);
	 build(1,1,n);
	 /*后续操作*/
    }
	return 0;
}

代码2（根据边权dfs序建树）