第4章 深度学习的数学基础
目录
4.6 矩阵
4.6 矩阵
下一章开始,我们就会用到矩阵。借助矩阵,可以用一个式子表示大量的联立方程式,特别方便。此外,使用矩阵或向量表示,也会更有助于我们直观理解方程式。

图4-13 标量、向量、矩阵、张量
4.6.1 什么是矩阵
把数横向或纵向排列,得到的是向量;把数像表格一样既横向排列又纵向排列,得到的就是矩阵。下式表示的是一个2×3矩阵(图4-14):
A
=
[
1
2
3
4
5
6
]
(4-70)
A=\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6\tag{4-70} \end{array}\right]
A=[142536](4-70)

图4-14 矩阵
通常,矩阵中横向的内容从上至下读作第1行、第2行等,纵向的内容从左至右读作第1列、第2列等。为了与Python中数组的索引一致,矩阵从0行0列开始计数,即横向从上至下分别是第0行、第1行等,纵向从左至右分别是第0列、第1列等。
式4-70所示的矩阵通常用“2行3列的矩阵”描述。当用一个变量表示矩阵时,一般用粗斜体的大写字母A表示。矩阵中元素的表示方法是:
[
A
]
i
,
j
(4-71)
[A]_{i, j}\tag{4-71}
[A]i,j(4-71)
该式表示的是矩阵A中第
i
i
i行第
j
j
j列的元素,如:
[
A
]
0
,
1
=
2
,
[
A
]
1
,
2
=
6
(4-72)
[A]_{0,1}=2,[A]_{1,2}=6\tag{4-72}
[A]0,1=2,[A]1,2=6(4-72)
请注意,元素的序号是从0开始的。
在用变量表示矩阵中的元素时,由于元素是标量,所以用斜体的小写字母表示:
A
=
[
a
0
,
0
a
0
,
1
a
0
,
2
a
1
,
0
a
1
,
1
a
1
,
2
]
(4-73)
\boldsymbol{A}=\left[\begin{array}{lll} a_{0,0} & a_{0,1} & a_{0,2} \\ a_{1,0} & a_{1,1} & a_{1,2}\tag{4-73} \end{array}\right]
A=[a0,0a1,0a0,1a1,1a0,2a1,2](4-73)
a i , j a_{i,j} ai,j的下标 i , j i,j i,j分别是行和列的序号。下标之间的“,”有时会省略,比如写作 a 01 a_{01} a01。
向量可以算作一种矩阵。比如,如下列向量可以看作一个3行1列的矩阵:
[
1
2
3
]
(4-74)
\left[\begin{array}{l} 1 \\ 2 \\ 3\tag{4-74} \end{array}\right]
123
(4-74)
而如下行向量可以看作一个1行2列的矩阵:
[
4
5
]
(4-75)
\begin{bmatrix} 4 & 5 \tag{4-75} \end{bmatrix}
[45](4-75)
4.6.2 矩阵的加法和减法
在介绍矩阵和联立方程式的关系之前,我们先介绍几个矩阵相关的规则。首先看一下矩阵的加法运算。下面以2×3矩阵A和B为例:
A
=
[
1
2
3
4
5
6
]
,
B
=
[
7
8
9
10
11
12
]
(4-76)
\boldsymbol{A}=\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right], \boldsymbol{B}=\left[\begin{array}{ccc} 7 & 8 & 9 \\ 10 & 11 & 12\tag{4-76} \end{array}\right]
A=[142536],B=[710811912](4-76)
矩阵的加法运算是把对应的元素相加(图4-15):
A
+
B
=
[
1
2
3
4
5
6
]
+
[
7
8
9
10
11
12
]
=
[
8
10
12
14
16
18
]
(4-77)
\boldsymbol{A}+\boldsymbol{B}=\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right]+\left[\begin{array}{ccc} 7 & 8 & 9 \\ 10 & 11 & 12 \end{array}\right]=\left[\begin{array}{ccc} 8 & 10 & 12 \\ 14 & 16 & 18 \tag{4-77} \end{array}\right]
A+B=[142536]+[710811912]=[81410161218](4-77)

图4-15 矩阵的加法和减法
减法运算与加法运算一样,是把对应的元素相减:
A
−
B
=
[
1
2
3
4
5
6
]
−
[
7
8
9
10
11
12
]
=
[
1
−
7
2
−
8
3
−
9
4
−
10
5
−
11
6
−
12
]
=
[
−
6
−
6
−
6
−
6
−
6
−
6
]
(4-78)
\boldsymbol{A}-\boldsymbol{B}=\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right]-\left[\begin{array}{ccc} 7 & 8 & 9 \\ 10 & 11 & 12 \end{array}\right]=\left[\begin{array}{ccc} 1-7 & 2-8 & 3-9 \\ 4-10 & 5-11 & 6-12 \end{array}\right]=\left[\begin{array}{ccc} -6 & -6 & -6 \\ -6 & -6 & -6 \tag{4-78} \end{array}\right]
A−B=[142536]−[710811912]=[1−74−102−85−113−96−12]=[−6−6−6−6−6−6](4-78)
无论是加法运算还是减法运算,两个矩阵的大小(行数和列数)必须相等。要想利用Python进行矩阵计算,必须和进行向量运算时一样,先使用import导入NumPy库。
# 代码清单 4-3-(1)
import numpy as np
然后,使用np.array定义矩阵。
# 代码清单 4-3-(2)
A=np.array([[1, 2, 3], [4, 5, 6]])
print(A)
输出结果:
[[1 2 3]
[4 5 6]]
在定义向量时,我们只是像np.array([1,2,3])这样用了一组[];而在定义矩阵时,则是先把每行的元素用一组[]括住,然后用[]把整个内容括起来,使用的是双层结构。下面定义矩阵B。
# 代码清单 4-3-(3)
B = np.array([[7, 8, 9], [10, 11, 12]])
print(B)
输出结果:
[[ 7 8 9]
[10 11 12]]
计算A+B、A-B:
# 代码清单 4-3-(4)
print(A + B)
print(A - B)
输出结果:
[[ 8 10 12]
[14 16 18]]
[[-6 -6 -6]
[-6 -6 -6]]
4.6.3 标量积
当矩阵乘以标量值时,结果是所有的元素都乘以标量值:
2
A
=
2
×
[
1
2
3
4
5
6
]
=
[
2
×
1
2
×
2
2
×
3
2
×
4
2
×
5
2
×
6
]
=
[
2
4
6
8
10
12
]
(4-79)
2 A=2 \times\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \end{array}\right]=\left[\begin{array}{lll} 2 \times 1 & 2 \times 2 & 2 \times 3 \\ 2 \times 4 & 2 \times 5 & 2 \times 6 \end{array}\right]=\left[\begin{array}{ccc} 2 & 4 & 6 \\ 8 & 10 & 12 \tag{4-79} \end{array}\right]
2A=2×[142536]=[2×12×42×22×52×32×6]=[28410612](4-79)

图4-16 矩阵的标量积
在Python中,矩阵的标量积代码如下:
# 代码清单 4-3-(5)
A = np.array([[1, 2, 3], [4, 5, 6]])
print(2 * A)
输出结果:
[[ 2 4 6]
[ 8 10 12]]
4.6.4 矩阵的乘积
矩阵之间的乘积(矩阵积)与加法或减法运算不同。
首先看一看1行三列的矩阵A和3行一列的矩阵B,这两个矩阵可以分别看作行向量和列向量,不过这里当作矩阵进行计算:
A = [ 1 2 3 ] , B = [ 4 5 6 ] (4-80) A=\left[\begin{array}{lll} 1 & 2 & 3 \end{array}\right], \boldsymbol{B}=\left[\begin{array}{l} 4 \\ 5 \\ 6 \tag{4-80} \end{array}\right] A=[123],B= 456 (4-80)

图4-17 1 × M 1\times M 1×M矩阵和 M × 1 M\times 1 M×1矩阵的乘积
这两个矩阵的乘积可以计算为:
A
B
=
[
1
2
3
]
[
4
5
6
]
=
1
×
4
+
2
×
5
+
3
×
6
=
32
(4-81)
A B=\left[\begin{array}{lll} 1 & 2 & 3 \end{array}\right]\left[\begin{array}{l} 4 \\ 5 \\ 6 \tag{4-81} \end{array}\right]=1 \times 4+2 \times 5+3 \times 6=32
AB=[123]
456
=1×4+2×5+3×6=32(4-81)
这就是把A和B当作向量时得到的内积。在Python中,A和B的内积如代码如下:
# 代码清单 4-3-(6)
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
print(A.dot(B))
#输出结果:32
计算A和B的内积用A.dot(B),A.dot(B)不仅可以计算向量内积,还可以计算矩阵积。但是这样的话,会产生一种对行向量A和B计算矩阵积的错觉。
其实,在Python中计算矩阵积时,矩阵的行和列会被自动调整为可以进行计算的形式。此时,B会被看作列向量,这样就可以继续计算内积了。
注意:如果使用通常的乘法运算符号“*”,则乘法运算会在对应的元素之间进行,如下代码所示:
# 代码清单 4-3-(7)
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
print(A * B)
#输出结果:[ 4 10 18]
这跟“+”或“-”相同。“/”也一样,是在对应的元素之间进行除法运算。演示代码如下:
# 代码清单 4-3-(8)
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])
print(A / B)
#输出结果:[0.25 0.4 0.5 ]
接下来,思考一下A为
2
×
3
2\times 3
2×3矩阵、B为
3
×
2
3\times 2
3×2矩阵时的情况:
A
=
[
1
2
3
−
1
−
2
−
3
]
,
B
=
[
4
−
4
5
−
5
6
−
6
]
\boldsymbol{A}=\left[\begin{array}{ccc} 1 & 2 & 3 \\ -1 & -2 & -3 \end{array}\right], \quad \boldsymbol{B}=\left[\begin{array}{cc} 4 & -4 \\ 5 & -5 \\ 6 & -6 \end{array}\right]
A=[1−12−23−3],B=
456−4−5−6
此时,我们把A看作2行的行向量,把B看作2列的列向量,并以各自的组合计算内积,然后在对应的位置写上答案。

图4-18 L × M L\times M L×M矩阵和 M × N M\times N M×N矩阵的乘积
具体的计算步骤如下:
A
B
=
[
1
2
3
−
1
−
2
−
3
]
[
4
−
4
5
−
5
6
−
6
]
=
[
1
×
4
+
2
×
5
+
3
×
6
1
×
(
−
4
)
+
2
×
(
−
5
)
+
3
×
(
−
6
)
(
−
1
)
×
4
+
(
−
2
)
×
5
+
(
−
3
)
×
6
(
−
1
)
×
(
−
4
)
+
(
−
2
)
×
(
−
5
)
+
(
−
3
)
×
(
−
6
)
]
=
[
32
−
32
−
32
32
]
\begin{aligned} A B &=\left[\begin{array}{ccc} 1 & 2 & 3 \\ -1 & -2 & -3 \end{array}\right]\left[\begin{array}{cc} 4 & -4 \\ 5 & -5 \\ 6 & -6 \end{array}\right] \\ &=\left[\begin{array}{cc} 1 \times 4+2 \times 5+3 \times 6 & 1 \times(-4)+2 \times(-5)+3 \times(-6) \\ (-1) \times 4+(-2) \times 5+(-3) \times 6 & \quad(-1) \times(-4)+(-2) \times(-5)+(-3) \times(-6) \end{array}\right] \\ &=\left[\begin{array}{cc} 32 & -32 \\ -32 & 32 \end{array}\right] \end{aligned}
AB=[1−12−23−3]
456−4−5−6
=[1×4+2×5+3×6(−1)×4+(−2)×5+(−3)×61×(−4)+2×(−5)+3×(−6)(−1)×(−4)+(−2)×(−5)+(−3)×(−6)]=[32−32−3232]
(
4
−
82
)
(4-82)
(4−82)
与前面一样,同样使用A.dot(B)计算。
# 代码清单 4-3-(9)
A = np.array([[1, 2, 3], [-1, -2, -3]])
B = np.array([[4, -4], [5, -5], [6, -6]])
print(A.dot(B))
输出结果:
[[ 32 -32]
[-32 32]]
在一般情况下,当A为 L × M L\times M L×M矩阵、B为 M × N M\times N M×N矩阵时,AB的大小为 L × N L\times N L×N。当A的列数与B的行数不等时,不能计算矩阵积。
矩阵积的元素
i
、
j
i、j
i、j计算为:
[
A
B
]
i
,
j
=
∑
m
=
0
M
−
1
a
i
,
m
b
m
,
j
(4-83)
[\boldsymbol{A} \boldsymbol{B}]_{i, j}=\sum_{m=0}^{M-1} a_{i, m} b_{m, j} \tag{4-83}
[AB]i,j=m=0∑M−1ai,mbm,j(4-83)
行数和列数相等的矩阵叫作方阵。当A和B均为方阵时,虽然我们可以计算出AB和BA的值,但是在一般情况下AB=BA是不成立的,所以在矩阵的乘法运算中,顺序很重要。从这一点来说,矩阵积与即使改变顺序答案也不变的标量积不同。
4.6.5 单位矩阵
对角元素均为1、其他元素均为0的特殊方阵叫作单位矩阵,用I表示,如
3
×
3
3\times3
3×3的单位矩阵为:
I
=
[
1
0
0
0
1
0
0
0
1
]
(4-84)
\boldsymbol{I}=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \tag{4-84} \end{array}\right]
I=
100010001
(4-84)

图4-19 单位矩阵
在Python中,np.identity(n)用于生成 n × n n\times n n×n的单位矩阵),示例如下:
# 代码清单 4-3-(10)
print(np.identity(3))
输出结果:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
print(np.eye(3))
输出结果:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
各个元素之后有” ⋅ \cdot ⋅”,这表示矩阵的元素可以是用于表示小数的float类型。
单位矩阵与标量“1”类似。任何数乘以1,结果都还是该数。单位矩阵也一样,任何矩阵(大小相同的方阵)与单位矩阵相乘,结果都不发生变化。比如,3×3矩阵与单位矩阵相乘:
[
1
2
3
4
5
6
7
8
9
]
[
1
0
0
0
1
0
0
0
1
]
=
[
1
+
0
+
0
0
+
2
+
0
0
+
0
+
3
4
+
0
+
0
0
+
5
+
0
0
+
0
+
6
7
+
0
+
0
0
+
8
+
0
0
+
0
+
9
]
=
[
1
2
3
4
5
6
7
8
9
]
\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{lll} 1+0+0 & 0+2+0 & 0+0+3 \\ 4+0+0 & 0+5+0 & 0+0+6 \\ 7+0+0 & 0+8+0 & 0+0+9 \end{array}\right]=\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{array}\right]
147258369
100010001
=
1+0+04+0+07+0+00+2+00+5+00+8+00+0+30+0+60+0+9
=
147258369
(4-85)
\tag{4-85}
(4-85)
计算代码如下:
# 代码清单 4-3-(11)
A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
I = np.identity(3)
print(A.dot(I))
输出结果:
[[1. 2. 3.]
[4. 5. 6.]
[7. 8. 9.]]
这里介绍单位矩阵,其实是为了给接下来要介绍的逆矩阵做铺垫。
4.6.6 逆矩阵
如何对矩阵进行除法运算呢?对于标量,除以3的运算与乘以3的倒数
1
3
\frac{1}{3}
31是一样的。一个数的倒数是与其相乘可以得到1的数。
a
a
a的倒数为
1
a
\frac{1}{a}
a1,也可以表示为
a
−
1
a^{-1}
a−1:
a
×
a
−
1
=
1
(4-86)
a \times a^{-1}=1\tag{4-86}
a×a−1=1(4-86)
与之类似,矩阵也有与其对应的逆矩阵。

图4-20 逆矩阵
但是,只有行数和列数相等的方阵才具有逆矩阵。一个方阵A与其逆矩阵 A − 1 \boldsymbol A^{-1} A−1相乘的结果为单位矩阵I:
A A − 1 = A − 1 A = I (4-87) \boldsymbol A \boldsymbol A^{-1}=\boldsymbol A^{-1} \boldsymbol A=\boldsymbol I\tag{4-87} AA−1=A−1A=I(4-87)
在一般情况下,矩阵积的结果与顺序有关,但一个矩阵与其逆矩阵的积一定是单位矩阵,所以与顺序无关。
比如,当A为2×2方阵时,令 A = [ a b c d ] \boldsymbol A=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right] A=[acbd],则A的逆矩阵为:
A − 1 = 1 a d − b c [ d − b − c a ] (4-88) \boldsymbol A^{-1}=\frac{1}{a d-b c}\left[\begin{array}{cc} d & -b \\ -c & a \tag{4-88} \end{array}\right] A−1=ad−bc1[d−c−ba](4-88)
如果 A = [ 1 2 3 4 ] \boldsymbol A=\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right] A=[1324],那么A的逆矩阵为:
A − 1 = 1 1 ⋅ 4 − 2 ⋅ 3 [ 4 − 2 − 3 1 ] = − 1 2 [ 4 − 2 − 3 1 ] = [ − 2 1 1.5 − 0.5 ] (4-89) \boldsymbol A^{-1}=\frac{1}{1 \cdot 4-2 \cdot 3}\left[\begin{array}{cc} 4 & -2 \\ -3 & 1 \end{array}\right]=-\frac{1}{2}\left[\begin{array}{cc} 4 & -2 \\ -3 & 1 \end{array}\right]=\left[\begin{array}{cc} -2 & 1 \\ 1.5 & -0.5 \tag{4-89} \end{array}\right] A−1=1⋅4−2⋅31[4−3−21]=−21[4−3−21]=[−21.51−0.5](4-89)
试着计算 A A − 1 \boldsymbol{AA}^{-1} AA−1,可得到单位矩阵:
A A − 1 = [ 1 2 3 4 ] ⋅ − 1 2 [ 4 − 2 − 3 1 ] = − 1 2 [ − 2 0 0 − 2 ] = [ 1 0 0 1 ] (4-90) \boldsymbol{A} \boldsymbol{A}^{-1}=\left[\begin{array}{ll} 1 & 2 \\ 3 & 4 \end{array}\right] \cdot-\frac{1}{2}\left[\begin{array}{cc} 4 & -2 \\ -3 & 1 \end{array}\right]=-\frac{1}{2}\left[\begin{array}{cc} -2 & 0 \\ 0 & -2 \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \tag{4-90} \end{array}\right] AA−1=[1324]⋅−21[4−3−21]=−21[−200−2]=[1001](4-90)
在Python中,np.linalg.inv(A)用于求A的逆矩阵:
# 代码清单 4-3-(12)
A = np.array([[1, 2], [3, 4]])
invA = np.linalg.inv(A)
print(invA)
输出结果:
[[-2. 1. ]
[ 1.5 -0.5]]
如上所示,得到的结果与上面的式4-89的结果一样。
这里必须注意,也有一些方阵没有对应的逆矩阵。如果是2×2方阵,那么使得 a d − b c = 0 ad-bc=0 ad−bc=0的矩阵就不存在逆矩阵。因为这样的话,式4-88中分数的分母就是0。
比如矩阵 [ 2 − 2 − 1 1 ] \left[\begin{array}{cc} 2 & -2 \\ -1 & 1 \end{array}\right] [2−1−21],由于 a d − b c = 0 ad-bc=0 ad−bc=0,所以它没有逆矩阵。
对于3×3和4×4等较大的矩阵,虽然也可以使用公式求逆矩阵,但是计算过程很复杂。因此,在机器学习中一般会借用库的力量,使用np.linalg.inv(A)求逆矩阵。
4.6.7 转置
将列向量转换为行向量、将行向量转换为列向量的转置运算,已在4.1节介绍。这个转置运算也可以扩展到矩阵中。
以下式为例说明一下:
A = [ 1 2 3 4 5 6 ] (4-91) \boldsymbol{A}=\left[\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6\tag{4-91} \end{array}\right] A=[142536](4-91)
把矩阵A的行和列互换,即可得到A的转置 A T \boldsymbol A^T AT,结果为(图4-23):
A T = [ 1 4 2 5 3 6 ] (4-92) \boldsymbol{A}^{\mathrm{T}}=\left[\begin{array}{ll} 1 & 4 \\ 2 & 5 \\ 3 & 6\tag{4-92} \end{array}\right] AT= 123456 (4-92)
Python实现代码如下:
# 代码清单 4-3-(13)
A = np.array([[1, 2, 3], [4, 5, 6]])
print(A)
print(A.T)
扩展到一般情况,转置之后,矩阵下标的顺序会被替换:
[ A ] i j = [ A T ] j i (4-93) [\boldsymbol{A}]_{i j}=\left[\boldsymbol{A}^{\mathrm{T}}\right]_{j i}\tag{4-93} [A]ij=[AT]ji(4-93)
在对AB整体进行转置时,如下关系式成立:
( A B ) T = B T A T (4-94) (\boldsymbol{A} \boldsymbol{B})^{\mathrm{T}}=\boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}\tag{4-94} (AB)T=BTAT(4-94)
转置之后矩阵积的顺序与转置前相反。以2×2矩阵为例,如下所示,可以证明式4-94成立:
( A B ) T = [ [ a 11 a 12 a 21 a 22 ] [ b 11 b 12 b 21 b 22 ] ] T = [ a 11 b 11 + a 12 b 21 a 21 b 11 + a 22 b 21 a 11 b 12 + a 12 b 22 a 21 b 12 + a 22 b 22 ] B T A T = [ b 11 b 21 b 12 b 22 ] [ a 11 a 21 a 12 a 22 ] = [ a 11 b 11 + a 12 b 21 a 21 b 11 + a 22 b 21 a 11 b 12 + a 12 b 22 a 21 b 12 + a 22 b 22 ] \begin{array}{l} (\boldsymbol{A B})^{\mathrm{T}}=\left[\left[\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]\left[\begin{array}{ll} b_{11} & b_{12} \\ b_{21} & b_{22} \end{array}\right]\right]^{\mathrm{T}}=\left[\begin{array}{ll} a_{11} b_{11}+a_{12} b_{21} & a_{21} b_{11}+a_{22} b_{21} \\ a_{11} b_{12}+a_{12} b_{22} & a_{21} b_{12}+a_{22} b_{22} \end{array}\right] \\ \boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}=\left[\begin{array}{ll} b_{11} & b_{21} \\ b_{12} & b_{22} \end{array}\right]\left[\begin{array}{ll} a_{11} & a_{21} \\ a_{12} & a_{22} \end{array}\right]=\left[\begin{array}{ll} a_{11} b_{11}+a_{12} b_{21} & a_{21} b_{11}+a_{22} b_{21} \\ a_{11} b_{12}+a_{12} b_{22} & a_{21} b_{12}+a_{22} b_{22} \end{array}\right] \end{array} (AB)T=[[a11a21a12a22][b11b21b12b22]]T=[a11b11+a12b21a11b12+a12b22a21b11+a22b21a21b12+a22b22]BTAT=[b11b12b21b22][a11a12a21a22]=[a11b11+a12b21a11b12+a12b22a21b11+a22b21a21b12+a22b22]
使用式4-94可以简单推导出:
( A B C ) T = C T ( A B ) T = C T B T A T (4-95) (\boldsymbol{A} \boldsymbol{B} \boldsymbol{C})^{\mathrm{T}}=\boldsymbol{C}^{\mathrm{T}}(\boldsymbol{A} \boldsymbol{B})^{\mathrm{T}}=\boldsymbol{C}^{\mathrm{T}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{A}^{\mathrm{T}}\tag{4-95} (ABC)T=CT(AB)T=CTBTAT(4-95)
这是把看作一个整体,先对与C进行转置,最后对AB进行转置。哪怕是三个矩阵的矩阵积,转置之后,矩阵下标的顺序也会被替换。
4.6.8 矩阵和联立方程式
借助矩阵,我们可以用一个式子表示大量的联立方程式,特别方便。到此为止的内容都是为使用矩阵做的铺垫,接下来,我们尝试用一个矩阵表示两个联立方程式,并使用矩阵运算求解答案。具体来说,这里以下面的联立方程式为例:
y
=
2
x
(4-96)
y=2x \tag{4-96}
y=2x(4-96)
y
=
−
x
+
3
(4-97)
y=-x+3 \tag{4-97}
y=−x+3(4-97)

图4-21 用矩阵表示法求解联立方程式
对于上面的联立方程式,把式4-96代入式4-97之后,可以简单地求出 x = 1 x=1 x=1, y = 2 y=2 y=2。这里特意通过矩阵的方式求解。首先,将式4-96和式4-97变形,得到:
2 x − y = 0 x + y = 3 (4-98) \begin{array}{l} 2 x-y=0\\ x+y=3 \tag{4-98} \end{array} 2x−y=0x+y=3(4-98)
上式可以表示为矩阵:
[
2
−
1
1
1
]
[
x
y
]
=
[
0
3
]
(4-99)
\left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} 0 \\ 3 \end{array}\right]\tag{4-99}
[21−11][xy]=[03](4-99)
为什么可以这样表示呢?计算式4-99的左边之后,可知下式成立,即两个列向量相等:
[
2
x
−
y
x
+
y
]
=
[
0
3
]
(4-100)
\left[\begin{array}{l} 2 x-y \\ x+y \end{array}\right]=\left[\begin{array}{l} 0 \\ 3 \end{array}\right]\tag{4-100}
[2x−yx+y]=[03](4-100)
式子左边和右边的向量相等,即矩阵中的对应元素相等,所以式4-100与式4-98是一个意思。
接下来,要想求出 x x x和 y y y的值,需要把式4-99变形为:
[ x y ] = [ ? ? ] \left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} ? \\ ? \end{array}\right] [xy]=[??]
因此,首先让式4-99的两边乘以$
\left[\begin{array}{cc}
2 & -1 \
1 & 1
\end{array}\right]
$的逆矩阵:
[ 2 − 1 1 1 ] − 1 [ 2 − 1 1 1 ] [ x y ] = [ 2 − 1 1 1 ] − 1 [ 0 3 ] (4-101) \left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]^{-1}\left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]^{-1}\left[\begin{array}{l} 0 \\ 3 \end{array}\right]\tag{4-101} [21−11]−1[21−11][xy]=[21−11]−1[03](4-101)
根据逆矩阵的性质可知,左边是一个单位矩阵:
[ 1 0 0 1 ] [ x y ] = [ 2 − 1 1 1 ] − 1 [ 0 3 ] (4-102) \left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]^{-1}\left[\begin{array}{l} 0 \\ 3 \end{array}\right]\tag{4-102} [1001][xy]=[21−11]−1[03](4-102)
已知单位矩阵乘以 [ x y ] T [x y]^{\mathrm{T}} [xy]T,结果不变,所以我们可以得到:
[ x y ] = [ 2 − 1 1 1 ] − 1 [ 0 3 ] \left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]^{-1}\left[\begin{array}{l} 0 \\ 3 \end{array}\right] [xy]=[21−11]−1[03]
通过公式4-88计算出如下所示的 [ 2 − 1 1 1 ] − 1 \left[\begin{array}{cc}2 & -1 \\ 1 & 1\end{array}\right]^{-1} [21−11]−1的结果:
[ 2 − 1 1 1 ] − 1 = 1 2 × 1 − ( − 1 ) × 1 [ 1 1 − 1 2 ] = 1 3 [ 1 1 − 1 2 ] \left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]^{-1}=\frac{1}{2 \times 1-(-1) \times 1}\left[\begin{array}{cc} 1 & 1 \\ -1 & 2 \end{array}\right]=\frac{1}{3}\left[\begin{array}{cc} 1 & 1 \\ -1 & 2 \end{array}\right] [21−11]−1=2×1−(−1)×11[1−112]=31[1−112]
然后得到:
[ x y ] = 1 3 [ 1 1 − 1 2 ] [ 0 3 ] = 1 3 [ 1 × 0 + 1 × 3 ( − 1 ) × 0 + 2 × 3 ] = [ 1 2 ] (4-103) \left[\begin{array}{l} x \\ y \end{array}\right]=\frac{1}{3}\left[\begin{array}{cc} 1 & 1 \\ -1 & 2 \end{array}\right]\left[\begin{array}{l} 0 \\ 3 \end{array}\right]=\frac{1}{3}\left[\begin{array}{l} 1 \times 0+1 \times 3 \\ (-1) \times 0+2 \times 3 \end{array}\right]=\left[\begin{array}{l} 1 \\ 2 \end{array}\right]\tag{4-103} [xy]=31[1−112][03]=31[1×0+1×3(−1)×0+2×3]=[12](4-103)
观察对应的元素可知,我们得到了正确的值,即 x = 1 x=1 x=1, y = 2 y=2 y=2。
对方程式求解时也需要变形,求出“ x = ? x=? x=?”。从这一点来说,这种方法与求解方程式的过程是类似的。对于方程式 a x = b ax=b ax=b,我们会在等式的两边都乘以 a a a的倒数,将其变形为 x = b / a x=b/a x=b/a的形式。而矩阵是让等式两边都从左边乘以逆矩阵,将$\boldsymbol{A}x= \boldsymbol B 变形 变形 变形x=\boldsymbol{A}^{-1}\boldsymbol{B}$的形式。
对于只有两个变量的两个联立方程式,即使用普通方法求解也不算麻烦,但是当变量和式子增多时,比如有 D D D个式子,这种使用矩阵的方法就会起到不凡的作用。
4.6.9 矩阵和映射
我们可以通过图形解释向量的加法或减法,同样地,也可以通过图形解释矩阵运算。矩阵可以看作“把向量转换为另一个向量的规则”。此外,如果将向量解释为坐标,即空间内的某个点,那么矩阵就可以解释为“令某点向别的点移动的规则”。
像这样关于从组(向量或点)到组(向量或点)的对应关系的规则叫作映射,矩阵的映射是一种线性映射。
比如,看一下上一节4-99矩阵方程式的左边,即式:
[ 2 − 1 1 1 ] [ x y ] \left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [21−11][xy]
将上式展开之后,可得到下式:
[ 2 − 1 1 1 ] [ x y ] = [ 2 x − y x + y ] (4-104) \left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} 2 x-y \\ x+y \end{array}\right]\tag{4-104} [21−11][xy]=[2x−yx+y](4-104)
因此矩阵 [ 2 − 1 1 1 ] \left[\begin{array}{cc}2 & -1 \\ 1 & 1\end{array}\right] [21−11]可以解释为一个令点 [ x y ] \left[\begin{array}{cc}x \\ y\end{array}\right] [xy]向点 [ 2 x − y x + y ] \left[\begin{array}{cc}2x-y \\ x+y\end{array}\right] [2x−yx+y]向点移动的映射。
比如,把向量 [ 1 , 0 ] T [1,0]^T [1,0]T代入式4-104之后,可得到 [ 2 , 1 ] T [2,1]^T [2,1]T,所以可以说点 [ 1 , 0 ] T [1,0]^T [1,0]T通过这个矩阵移动到点 [ 2 , 1 ] T [2,1]^T [2,1]T。同样,也可以说点 [ 0 , 1 ] T [0,1]^T [0,1]T通过这个矩阵移动到 [ − 1 , − 1 ] T [-1,-1]^T [−1,−1]T,点 [ 1 , 2 ] T [1,2]^T [1,2]T通过这个矩阵移动到 [ 0 , 3 ] T [0,3]^T [0,3]T。像这样从各种点移动的情形如图4-22中的左图所示,形状为由内向外的旋涡状。
图4-22中的右图为 [ 2 − 1 1 1 ] \left[\begin{array}{cc}2 & -1 \\ 1 & 1\end{array}\right] [21−11]的逆矩阵的映射,它是由外向内的旋涡状,与原矩阵的映射的移动方向刚好相反。
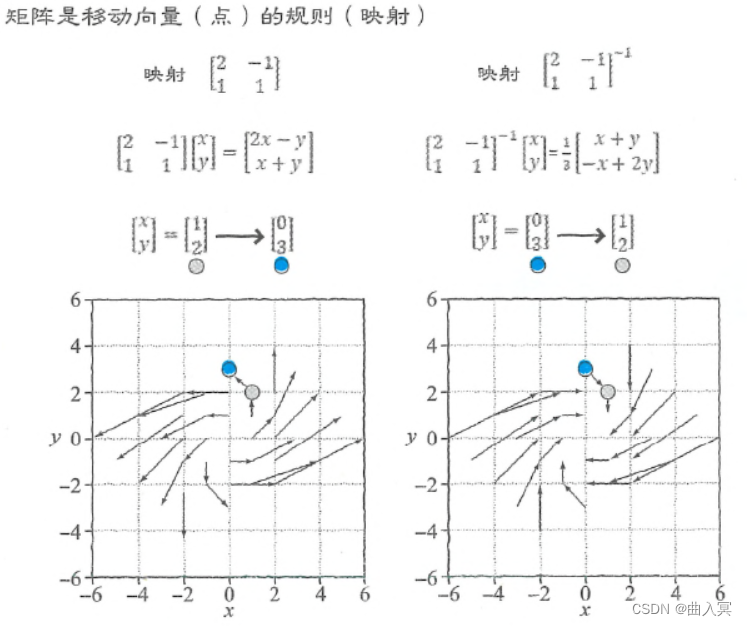
图4-22 矩阵形式的向量的映射
这里,式4-99可以解释为这样一个问题:应用矩阵 [ 2 − 1 1 1 ] \left[\begin{array}{cc}2 & -1 \\ 1 & 1\end{array}\right] [21−11]的映射规则被移动到 [ 0 3 ] \left[\begin{array}{cc}0 \\ 3\end{array}\right] [03]的是哪个点?
[ 2 − 1 1 1 ] [ x y ] = [ 0 3 ] \left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{l} 0 \\ 3 \end{array}\right] [21−11][xy]=[03]
答案为:
[ x y ] = [ 2 − 1 1 1 ] − 1 [ 0 3 ] = [ 1 2 ] \left[\begin{array}{l} x \\ y \end{array}\right]=\left[\begin{array}{cc} 2 & -1 \\ 1 & 1 \end{array}\right]^{-1}\left[\begin{array}{l} 0 \\ 3 \end{array}\right]=\left[\begin{array}{l} 1 \\ 2 \end{array}\right] [xy]=[21−11]−1[03]=[12]
我们可以这样理解:通过逆矩阵把移动后的点 [ 0 3 ] \left[\begin{array}{cc}0 \\ 3\end{array}\right] [03]恢复到动前的位置可知,移动前的位置是点 [ 1 2 ] \left[\begin{array}{cc}1 \\ 2\end{array}\right] [12]。