关卡名	认识贪心思想	我会了✔️
内容	1.复习一维数组，对数组进行多轮插入或者删除时会频繁移动数据，理解双指针是如何避免该问题的	✔️
	2.理解滑动窗口的原理和适用场景	✔️
	3.掌握窗口变与不变的两种情况是如何用来解题的	✔️

1.难以解释的贪心算法 

贪心的思想非常不好解释，而且越使用权威的语言解释越难懂。而且做题的时候根据自己的理解直接做可能能做出来，而非要解释一下怎么使用的贪心的话反而懵圈了。
更郁闷的是贪心的题目没有固定的套路，一题一样，好在大部分的贪心算法题不是特别难，因此公认的贪心学习法则是”直接做题，不考虑贪不贪心“，本章我们就从一些经典题目中寻找一些“哲学规律”。
贪婪算法(贪心算法)是指在对问题进行求解时，在每一步选择中都采取最好或者最优(即最有利)的选择，从而希望能够导致结果是最好或者最优的算法；贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解)，但是都是相对近似(接近)最优解的结果。
那贪心是否一定能得到最优解呢？《算法导论》给出了最明确的答案——贪心算法不能保证一定能得到最优解，但是对很多问题确实可以得到最优解 。
既然不能保证 ，我怎么知道某个解法是不是最优解呢？很遗憾，笔者查阅大量材料，也没有谁给出定论，大部分的解释其实就是——看上去是就是了。
那我怎么知道什么时候该用贪心呢？这要求要解决的问题具有”最优子结构“，那什么是”最优子结构“呢？这个问题好比用高等数学证明”1+1=2“，解释不如不解释。
既然贪心这么邪门，那该怎么学呢？笔者的观点是将常见的贪心题都找出来看看大致是什么样子的，面试经常遇到的贪心题目也是有限的，我们找出来学一学就行了。
贪心常见的经典应用场景有如下这些，这些算法很多与图有关，本身比较复杂，也难以实现 ，我们一般掌握其思想即可：
1.排序问题：选择排序、拓扑排序2.优先队列：堆排序3.赫夫曼压缩编码4.图里的Prim、Fruskal和Dijkstra算法5.硬币找零问题6.分数背包问题7.并查集的按大小或者高度合并问题或者排名8.任务调度部分场景9.一些复杂问题的近似算法
所以贪心就像太极，无招胜有招，根据具体的题目特点直接想怎么做就行，不用考虑其他的。

2.贪心问题举例

2.1 分发饼干

我们先看一个简单的题目，LeetCode455，分发饼干：假设你要给孩子们一些小饼干。但是每个孩子最多只能给一块饼干。每个孩子的饭量不同，对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。示例：
其中g是胃口，s是拥有的饼干。

输入: g = [1,2,3], s = [1,1]

输出: 1

解释:

你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。

虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。所以你应该输出1。

这里既要满足小孩的胃口，也不要造成饼干尺寸的浪费。大尺寸的饼干既可以满足胃口大的孩子也可以满足胃口小的孩子，那么就应该优先满足胃口大的。这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。
所以，这里可以使用贪心策略，先将饼干数组和小孩数组排序。 然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量就可以了。也就是这样：

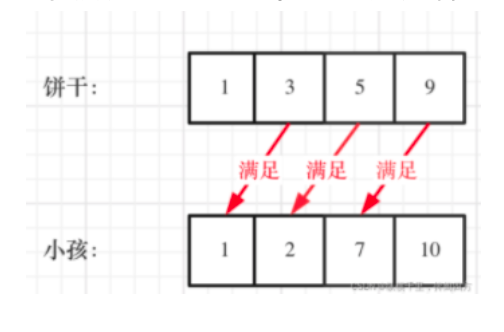
这里我们就考虑胃口，大饼干先喂饱大胃口，最后看能满足几个孩子的需要就行。

//g是孩子的胃口数组，s是拥有的饼干数组
public int findContentChildren(int[] g, int[] s) {
    Arrays.sort(g);
    Arrays.sort(s);
    int count = 0;
    int start = s.length - 1;
    // 遍历孩子的胃口
    for(int index=g.length-1;index>=0;index--){
        if(start>=0 && g[index]<=s[start]){
            start--;
            count++;
        }
    }
    return count;
}

2.2 柠檬水找零

这也是贪心的典型题目之一，先看题目要求：LeetCode860，在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。
注意，一开始你手头没有任何零钱。给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例1：

输入：bills = [5,5,5,10,20]

输出：true

解释：

前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。

第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。

第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。

由于所有客户都得到了正确的找零，所以我们输出 true。

示例2：

输入：bills = [5,5,10,10,20]

输出：false

解释：

前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。

对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。

对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。

由于不是每位顾客都得到了正确的找零，所以答案是 false。

这个题描述有点啰嗦，但是根据示例，不难看懂。这个题给小学生是不是也会做呢？然后当我们分析如何用代码实现时会有点懵，其实主要有三种情况：

• 1.如果给的是5，那么直接收下。
• 2.如果给的是10元，那么收下一个10，给出一个5，此时必须要有一个5才行。
• 3.如果给的是20，那么优先消耗一个10元，再给一个5元。假如没有10元，则给出3个5元。

上面情况三里，有10就先给10，没有才给多个5，这就是贪心选择的过程。为什么要优先消耗一个10和一个5呢？小学生都知道因为10只能给账单20找零，而5可以给账单10和账单20找零，5更万能！所以这里的局部最优就是遇到账单20，优先消耗美元10，完成本次找零。
这就是局部最优可以推出全局最优，代码如下： 

public boolean lemonadeChange(int[] bills) {
//这里只表示5元和10元纸币的数量，而不是总金额
    int cash_5 = 0;
    int cash_10 = 0;
    for(int i=0;i<bills.length;i++){
        if(bills[i]==5){
            cash_5++;
        } else if(bills[i]==10){
            cash_5--;
            cash_10++;
        } else if(bills[i]==20){
            if(cash_10>0){
                cash_10--;
                cash_5--;
            } else {
                cash_5 -= 3;
            }
        }
        if(cash_5<0 || cash_10<0) return false;
    }
    return ture;
}

2.3 分发糖果 

这个题目虽然官方标记是困难，但其实特别简单。LeetCode135：n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。你需要按照以下要求，给这些孩子分发糖果，并返回需要准备的 最少糖果数目：

• 每个孩子至少分配到 1 个糖果。
• 相邻两个孩子评分更高的孩子会获得更多的糖果。

 示例1：

输入：ratings = [1,0,2]

输出：5

解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

示例2：

输入：ratings = [1,2,2]

输出：4

解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。

第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

首先我们来看这个题是什么意思。假如有5个孩子，因为每个孩子至少一个糖果，所以一定要花出去的最少糖果是{1,1,1,1,1} 一共5个。
然后是相邻孩子评分更高的能获得更多的糖果。假如评分为{1,2,3,2}，则最少花出去的糖果为{1,2,3,1}，因为前三个评分在增加，则糖果必须递增，因此分别要发的糖果最少为{1,2,3}个，最后一个因为评分低了，所以我们给最少1个。
另外，假如评分相等，例如{1,2,2,2,2,}，根据题目要求，则后面重复的都给一个的就行了，也就是分别给{1,2,1,1,1}个。
首先，我们根据题意从左向后依次比较，确定第一轮要预发的糖果数量，只要右边的比左边的大，就一直加1；如果右边比左边小，就设置为1 ，然后继续向右比较。结果如下：

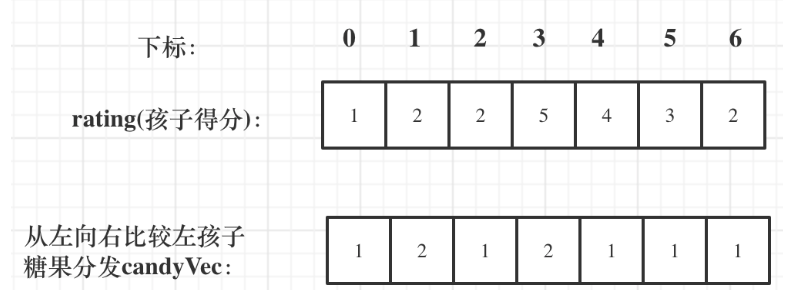此时有人就有疑问了，题目是要求相邻的孩子评分高的孩子必须获得更多的糖果，上面序列的后面几个评分为 4 、3、 2 但是得到的糖果却是一样的，那怎么办呢？
很简单， 我们在上面的基础上，再从右向左走一轮。如果左边的比右边的小，则不管。如果左边的比右边的大，则不是简单的加一，而是要在{i+1}的基础上，先加1再赋值给{i}。看例子：
最后四个评分为 {5 4 3 2 }，第一轮结束之后应该发的糖果为left={2,1,1,1}。
如果当我们只考虑从右向左的时候，很显然：

• 最后一个评分为2得到1个糖果
• 倒数第二个评分为3，得到2个糖果
• 倒数第三个评分为4，得到2+1=3个糖果
• 倒数第四个评分为5，得到3+1=4个糖果

因此最后四个的right={4,3,2,1}，接下来每个位置i我们只要从left[i]和right[i]中选最大就行了。不过这里我们其实不用两个数组，一个数组更新两次即可，首先从左向后给数组candyVec赋值，然后再从右向左更新数组元素，每次赋值之前先比较一下取max即可。如下图： 

public static int candy(int[] ratings) {
        int[] candyVec = new int[ratings.length];
        candyVec[0] = 1;
        for (int i = 1; i < ratings.length; i++) {
            if (ratings[i] > ratings[i - 1]) {
                candyVec[i] = candyVec[i - 1] + 1;
            } else {
                candyVec[i] = 1;
            }
        }
        for (int i = ratings.length - 2; i >= 0; i--) {
            if (ratings[i] > ratings[i + 1]) {
                candyVec[i] = Math.max(candyVec[i], candyVec[i + 1] + 1);
            }
        }
        int ans = 0;
        for (int s : candyVec) {
            ans += s;
        }
        return ans;
}