单调栈结构

news2024/11/27 14:28:59

单调栈
单调栈是一种特殊设计的栈结构，为了解决如下的问题：
给定一个可能含有重复数值的 arr[]，i位置的数一定存在如下两种信息：

arr[i]的左侧离 i 最近并且小于（或者大于）arr[i] 的数在哪？
arr[i]的右侧离 i 最近并且小于（或者大于）arr[i] 的数在哪？

如果想要得到arr[]中所有元素的这两个位置的信息，怎么能让得到信息的过程尽可能的快？

单调栈的实现

无重复值
拿左右侧距离arr[i]最近并且小于arr[i]来举例
假设当前有数组arr[] = {3,1,5,7,2,6,4}，从0 ~ N-1顺序遍历。而我们的单调栈严格保持着栈底到栈顶是由小到大的顺序，此时栈中为null，所以0位置的3直接放入栈中。
在这里插入图片描述
下一个1位置1，如果此时将1放入栈中破坏了小 -> 大的栈结构，所以将0位置3弹出，弹出时收集0 - 3的左右侧距离最近的小于当前元素的信息。0 - 3弹出后栈中无元素，证明左侧没有比它小的，所以为 -1，右侧最近为1，此时弹出0->3 将 1-1放入栈中。
在这里插入图片描述
继续向下，数组下标2位置的5和3位置的7都可以保证栈由小到大的顺序，所以按照顺序放入栈中即可。此时数组下标来到了4位置的2。

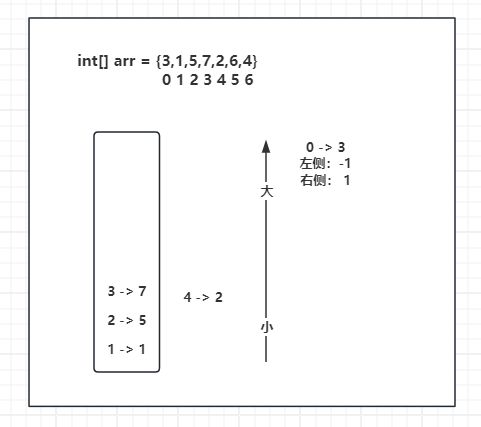
4 - 2如果想要放入栈中，会破坏由小到大的顺序，所以此时弹出栈顶元素 3 - 7，3 - 7右侧最近并且小于当前元素的值为 4 - 2，左侧最近且小的元素为当前栈顶元素 2 - 5 ，3 - 7元素左右侧信息收集完成。
此时4 - 2依然不能放入栈中，因为当前栈顶元素为2 - 5，弹出栈顶元素2 - 5，收集 2 - 5 的信息，同样的，4 - 2元素过来导致的2 - 5元素出栈，所以 4 - 2 元素为2 - 5的右侧最近且小于当前元素的值。此时栈中剩余元素 1 - 1，所以2 - 5 右侧信息 4 - 2 左侧信息 1 -1。
栈中剩余元素 1 - 1，4 - 2放入满足条件，直接入栈。
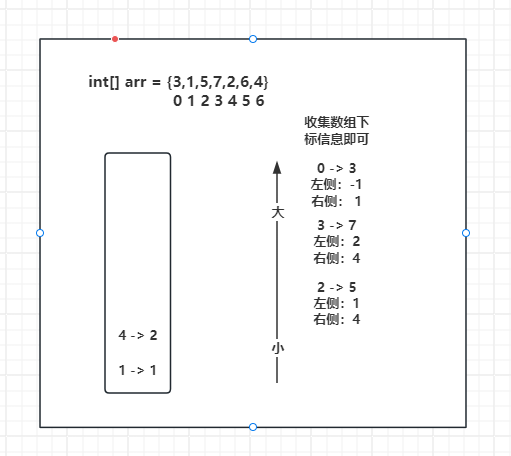
在这里插入图片描述
下一个元素 5 - 6直接入栈，来到最后一个元素 6 - 4。

来看6 - 4，此时栈顶元素 5 - 6，直接入栈不符合有小到大要求，所以弹出栈顶元素 5 - 6，收集 5 - 6信息，6 - 4元素的到来导致的5 - 6元素的出栈，所以6 - 4为 5 - 6的右侧最近且小的元素，此时栈顶元素4 - 2为左侧最近且小的元素，收集好5 -6信息后，6 - 4元素入栈。
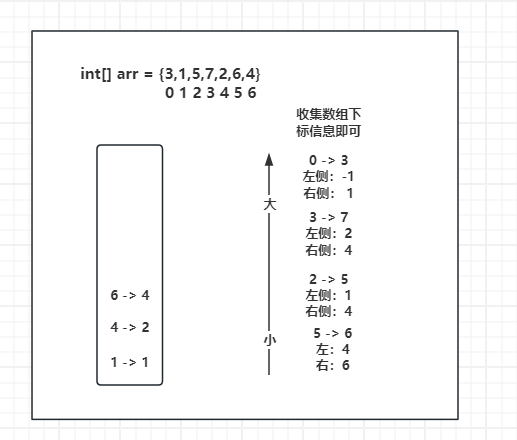
在这里插入图片描述
此时数组已经遍历完了，接下来怎么办？循环弹出栈中元素，把栈弹空即可。
因为此时已经不会再有新的元素加进来，所以栈中剩余元素的右侧最近且小的值都为 - 1。
弹出 6 - 4后，栈顶元素为 4 - 2，所以 4 - 2是6 - 4左侧最近且小的元素，右侧为-1。
弹出 4 - 2后，栈顶元素为1 - 1，所以 1 - 1是 4 - 2左侧最近且小的元素，右侧为 -1。
最后剩的元素1 - 1，弹出后栈为null，所以1 - 1左右两侧都没有最近且小的值， -1 -1。
数组中所有元素左右侧信息收集完毕。
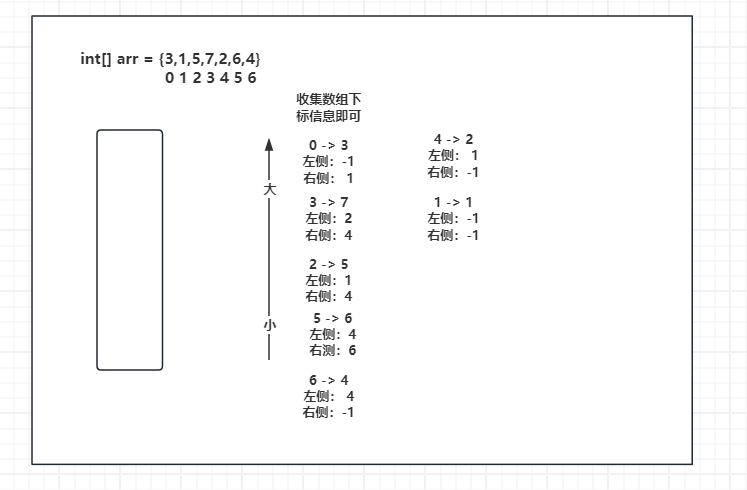
在这里插入图片描述

证明（数组中无重复值）
我们来验证一下上面所说的流程，看它为什么是对的。
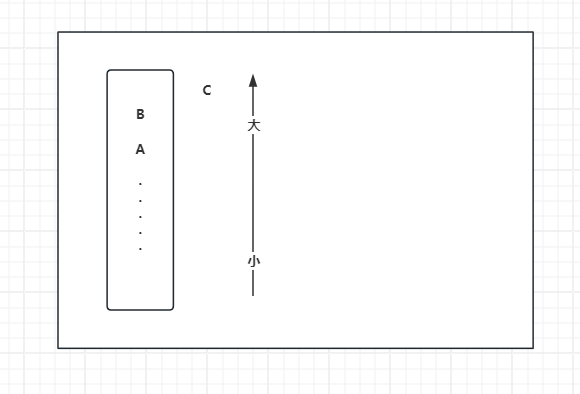
假设在某一步，B下面是A，此时由于C的到来B要出栈，此时要收集B的信息。

为什么C会是B右侧最近且小的数。

C为什么会使B弹出？由于我们单调栈的特性，所以一定是因为B的值大于C，并且是从数组0位置开始到 N - 1位置遍历，所以说数组中C一定在B的右边。
B和C中间的数有没有可能小于B？也不可能，如果BC中间有小于B的数，那B早就会被弹出栈，不会等C过来的时候才出栈。所以C才是B右边最近且小于B的数。

为什么B左边比它小的是A？

因为在栈中B在A的上面，所以在数组中B一定在A的右边。
A和B中间的数，有没有可能小于A？不可能，如果有这样的数，A早就会出栈，不会B下面压着A。
A和B中间的数，有没有大于A 小于B？也不可能，比如说A = 3 B = 7，在数组中是3 5 4 7这样的顺序。3进栈后5紧接着也会跟着进栈，但是到4的时候，5虽然出栈了，不过等7进栈时，B不会压着A，中间还会有个4，B能直接压着A说明AB中间没有大于A小于B的数。
A和B中间的数都是大于B的，B下面压着A，A在B的左边，那A不就是B左边最近且小的值么？

数组中有重复值
如果数组中有重复值该怎么弄？栈中存一个链表结构，相同值的数组下标放在一起，来看下面的图。
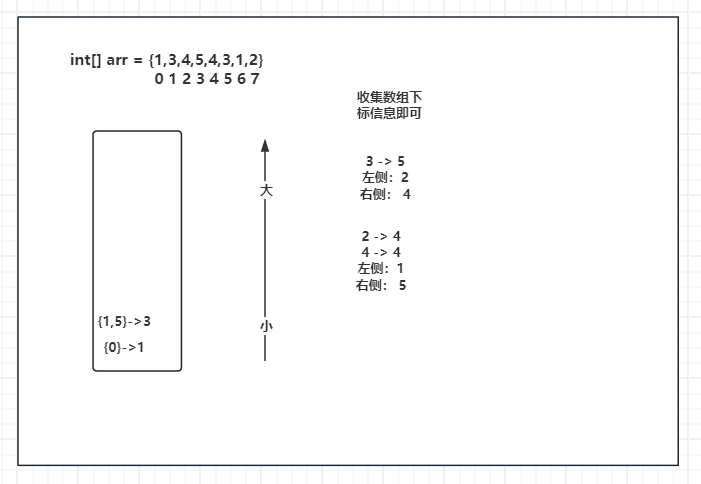
假设数组int[] arr = {1,3,4,5,4,3,1,2}，刚来上0 - 1时，栈中为null，直接入栈，后面的3 4 5同样符合栈中元素从小到大的顺序，一次入栈。此时来到了数组下标位置为4的元素。
在这里插入图片描述
4 - 4小于当前栈顶元素 3 - 5，弹出栈顶元素，此时结算3 - 5元素的信息，因为是 4 - 4元素的到来导致我出栈的，所以我右侧最近且小的信息是4 - 4，左侧最近且小的元素为栈中下一个元素的链表中最后一个元素，在这里是2 - 4，所以3 - 5左侧最近且小的值2 - 4，右侧最近且小的值 4 - 4。还没完，此时栈顶元素2 - 4的值和4 - 4的值相等，统一放在链表中。
在这里插入图片描述
接下往下走，来到了5 - 3，此时栈顶元素大于当前值5 - 3，弹出栈顶元素，2 - 4和4 - 4两个值一起结算，因为是5 - 3的到来导致我们两个出栈，所以右侧最近且小的值为5- 3，左侧最近且小的值，依然是找栈中下一个元素的链表中的最后一个元素，在这里是1 - 3，一起结算的相同值的左右最近且最小元素一定是一样的，所以2 - 4和4 - 4左侧最近且小的值为1 - 3，右侧近且小的值为5 - 3。弹出后，5 - 3压入栈中。
在这里插入图片描述
在往下走，来到了6 - 1，同样处理，1 - 3 和 5 - 3 弹出，一起结算，左侧最近且小的值为 0 - 1，右侧最近且小的值为 6 - 1。6 - 1压入栈中。

最后7 - 2直接入栈。数组遍历到头了，循环遍历直接弹出栈中元素。依然是没有新的元素加入，所以栈中剩余元素所有的右侧最近且小的值为-1。
7 - 2左侧最近且小的值，看栈中下一个元素的链表中最后一个元素，在这里为 6 - 1，所以 7 - 2的左侧最近且小的值为 6 - 1，右侧最近且小为 -1。
剩余的 0 - 1元素和 6 - 1元素，左右最近且小的值都为-1。
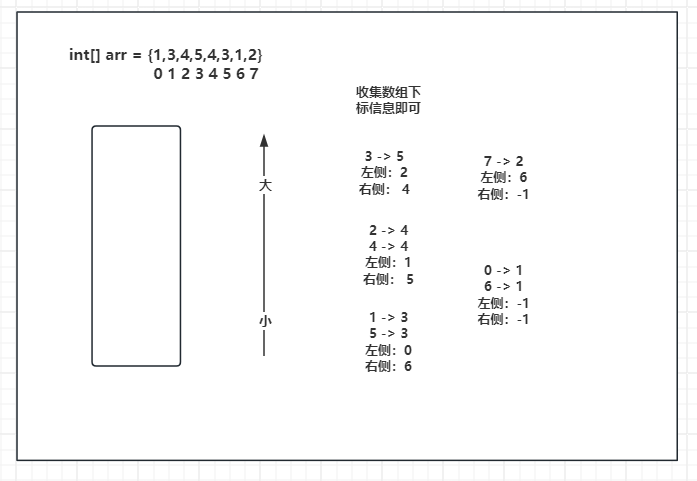
在这里插入图片描述
数组中元素信息全部收集完成。

总结
那个元素使栈中元素弹出，即为弹出元素的右侧最近且小的值，弹出后的栈顶元素为弹出元素的左侧最近且小的值。数组长度为N，遍历完整个数组，所有元素再栈中最多进一次出一次，所以时间复杂度为 $O (N)$ 。
如果数组中有重复值，则用链表维护相同值的元素下标。

代码
返回的二维数组中第一个数组代表arr中的下标，每个数组对应的第二个数组中一共两个值，0表示左侧最近且小，1表示右侧最近且小。
[
0 : [-1, 1]
1 : [-1, -1]
2 : [ 1, -1]
3 : [ 2, -1]
]
无重复值

 public static int[][] getNearLessNoRepeat(int[] arr) {
        int[][] result = new int[arr.length][2];

        Stack<Integer> stack = new Stack<>();
        for (int i = 0; i < arr.length; i++) {
            while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {
                Integer cur = stack.pop();
                Integer leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
                result[cur][0] = leftLessIndex;
                result[cur][1] = i;
            }
            stack.push(i);
        }
        while (!stack.isEmpty()) {
            Integer cur = stack.pop();
            Integer leftLessIndex = stack.isEmpty() ? -1 : stack.peek();
            result[cur][0] = leftLessIndex;
            result[cur][1] = -1;
        }
        return result;
    }

有重复值

 public static int[][] getNearLess(int[] arr) {
        int[][] res = new int[arr.length][2];
        Stack<List<Integer>> stack = new Stack<>();

        for (int i = 0; i < arr.length; i++) {
            while (!stack.isEmpty() && arr[stack.peek().get(0)] > arr[i]) {
                List<Integer> linked = stack.pop();
                Integer leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);

                for (Integer cur : linked) {
                    res[cur][0] = leftLessIndex;
                    res[cur][1] = i;
                }
            }
            if (!stack.isEmpty() && stack.peek().get(0) == i) {
                stack.peek().add(Integer.valueOf(i));
            } else {
                ArrayList<Integer> list = new ArrayList<>();
                list.add(i);
                stack.push(list);
            }
        }

        while (!stack.isEmpty()) {
            List<Integer> lists = stack.pop();
            Integer leftLessIndex = stack.isEmpty() ? -1 : stack.peek().get(stack.peek().size() - 1);

            for (Integer cur : lists) {
                res[cur][0] = leftLessIndex;
                res[cur][1] = -1;
            }
        }
        return res;
    }