二叉搜索树中第K小的元素[中等]

优质博文：IT-BLOG-CN

一、题目

给定一个二叉搜索树的根节点root，和一个整数k，请你设计一个算法查找其中第k个最小元素（从1开始计数）。

示例 1：

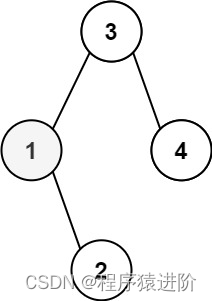
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

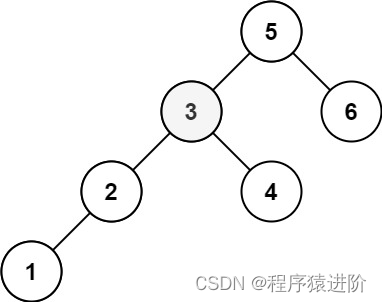
输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

树中的节点数为n。
1 <= k <= n <= 104
0 <= Node.val <= 104

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

二、代码

【1】中序遍历： 二叉搜索树具有如下性质：
● 结点的左子树只包含小于当前结点的数。
● 结点的右子树只包含大于当前结点的数。
● 所有左子树和右子树自身必须也是二叉搜索树。

二叉树的中序遍历即按照访问左子树——根结点——右子树的方式遍历二叉树；在访问其左子树和右子树时，我们也按照同样的方式遍历；直到遍历完整棵树。

思路和算法： 因为二叉搜索树和中序遍历的性质，所以二叉搜索树的中序遍历是按照键增加的顺序进行的。于是，我们可以通过中序遍历找到第k个最小元素。

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
        while (root != null || !stack.isEmpty()) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            --k;
            if (k == 0) {
                break;
            }
            root = root.right;
        }
        return root.val;
    }
}

时间复杂度： 时间复杂度：O(H+k)，其中H是树的高度。在开始遍历之前，我们需要O(H)到达叶结点。当树是平衡树时，时间复杂度取得最小值O(log⁡N+k)；当树是线性树（树中每个结点都只有一个子结点或没有子结点）时，时间复杂度取得最大值O(N+k)。
空间复杂度： O(H)，栈中最多需要存储H个元素。当树是平衡树时，空间复杂度取得最小值O(log⁡N)；当树是线性树时，空间复杂度取得最大值O(N)。

【2】记录子树的结点数： 如果你需要频繁地查找第k小的值，你将如何优化算法？

思路和算法： 在方法一中，我们之所以需要中序遍历前k个元素，是因为我们不知道子树的结点数量，不得不通过遍历子树的方式来获知。因此，我们可以记录下以每个结点为根结点的子树的结点数，并在查找第k小的值时，使用如下方法搜索：
● 令node等于根结点，开始搜索。
● 对当前结点node进行如下操作：
○ 如果node的左子树的结点数left小于k−1，则第k小的元素一定在node的右子树中，令node等于其的右子结点，k等于k−left−1，并继续搜索；
○ 如果node的左子树的结点数left等于k−1，则第k小的元素即为node，结束搜索并返回node即可；
○ 如果node的左子树的结点数left大于k−1，则第k小的元素一定在node的左子树中，令node等于其左子结点，并继续搜索。

在实现中，我们既可以将以每个结点为根结点的子树的结点数存储在结点中，也可以将其记录在哈希表中。

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        MyBst bst = new MyBst(root);
        return bst.kthSmallest(k);
    }
}

class MyBst {
    TreeNode root;
    Map<TreeNode, Integer> nodeNum;

    public MyBst(TreeNode root) {
        this.root = root;
        this.nodeNum = new HashMap<TreeNode, Integer>();
        countNodeNum(root);
    }

    // 返回二叉搜索树中第k小的元素
    public int kthSmallest(int k) {
        TreeNode node = root;
        while (node != null) {
            int left = getNodeNum(node.left);
            if (left < k - 1) {
                node = node.right;
                k -= left + 1;
            } else if (left == k - 1) {
                break;
            } else {
                node = node.left;
            }
        }
        return node.val;
    }

    // 统计以node为根结点的子树的结点数
    private int countNodeNum(TreeNode node) {
        if (node == null) {
            return 0;
        }
        nodeNum.put(node, 1 + countNodeNum(node.left) + countNodeNum(node.right));
        return nodeNum.get(node);
    }

    // 获取以node为根结点的子树的结点数
    private int getNodeNum(TreeNode node) {
        return nodeNum.getOrDefault(node, 0);
    }
}

时间复杂度： 预处理的时间复杂度为O(N)，其中N是树中结点的总数；我们需要遍历树中所有结点来统计以每个结点为根结点的子树的结点数。搜索的时间复杂度为O(H)，其中H是树的高度；当树是平衡树时，时间复杂度取得最小值O(log⁡N)；当树是线性树时，时间复杂度取得最大值O(N)。
空间复杂度： O(N)，用于存储以每个结点为根结点的子树的结点数。

【3】平衡二叉搜索树： 如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第k小的值，你将如何优化算法？

方法三需要先掌握平衡二叉搜索树（AVL树）的知识。平衡二叉搜索树具有如下性质：
● 平衡二叉搜索树中每个结点的左子树和右子树的高度最多相差1；
● 平衡二叉搜索树的子树也是平衡二叉搜索树；
● 一棵存有 nnn 个结点的平衡二叉搜索树的高度是O(log⁡n)。

思路和算法： 我们注意到在方法二中搜索二叉搜索树的时间复杂度为O(H)，其中H是树的高度；当树是平衡树时，时间复杂度取得最小值O(log⁡N)。因此，我们在记录子树的结点数的基础上，将二叉搜索树转换为平衡二叉搜索树，并在插入和删除操作中维护它的平衡状态。

class Solution {
    public int kthSmallest(TreeNode root, int k) {
        // 中序遍历生成数值列表
        List<Integer> inorderList = new ArrayList<Integer>();
        inorder(root, inorderList);

        // 构造平衡二叉搜索树
        AVL avl = new AVL(inorderList);

        // 模拟1000次插入和删除操作
        int[] randomNums = new int[1000];
        Random random = new Random();
        for (int i = 0; i < 1000; ++i) {
            randomNums[i] = random.nextInt(10001);
            avl.insert(randomNums[i]);
        }
        shuffle(randomNums); // 列表乱序
        for (int i = 0; i < 1000; ++i) {
            avl.delete(randomNums[i]);
        }

        return avl.kthSmallest(k);
    }

    private void inorder(TreeNode node, List<Integer> inorderList) {
        if (node.left != null) {
            inorder(node.left, inorderList);
        }
        inorderList.add(node.val);
        if (node.right != null) {
            inorder(node.right, inorderList);
        }
    }

    private void shuffle(int[] arr) {
        Random random = new Random();
        int length = arr.length;
        for (int i = 0; i < length; i++) {
            int randIndex = random.nextInt(length);
            int temp = arr[i];
            arr[i] = arr[randIndex];
            arr[randIndex] = temp;
        }
    }
}

// 平衡二叉搜索树（AVL树）：允许重复值
class AVL {
    Node root;

    // 平衡二叉搜索树结点
    class Node {
        int val;
        Node parent;
        Node left;
        Node right;
        int size;
        int height;

        public Node(int val) {
            this(val, null);
        }

        public Node(int val, Node parent) {
            this(val, parent, null, null);
        }

        public Node(int val, Node parent, Node left, Node right) {
            this.val = val;
            this.parent = parent;
            this.left = left;
            this.right = right;
            this.height = 0; // 结点高度：以node为根节点的子树的高度（高度定义：叶结点的高度是0）
            this.size = 1; // 结点元素数：以node为根节点的子树的节点总数
        }
    }

    public AVL(List<Integer> vals) {
        if (vals != null) {
            this.root = build(vals, 0, vals.size() - 1, null);
        }
    }

    // 根据vals[l:r]构造平衡二叉搜索树 -> 返回根结点
    private Node build(List<Integer> vals, int l, int r, Node parent) {
        int m = (l + r) >> 1;
        Node node = new Node(vals.get(m), parent);
        if (l <= m - 1) {
            node.left = build(vals, l, m - 1, node);
        }
        if (m + 1 <= r) {
            node.right = build(vals, m + 1, r, node);
        }
        recompute(node);
        return node;
    }

    // 返回二叉搜索树中第k小的元素
    public int kthSmallest(int k) {
        Node node = root;
        while (node != null) {
            int left = getSize(node.left);
            if (left < k - 1) {
                node = node.right;
                k -= left + 1;
            } else if (left == k - 1) {
                break;
            } else {
                node = node.left;
            }
        }
        return node.val;
    }

    public void insert(int v) {
        if (root == null) {
            root = new Node(v);
        } else {
            // 计算新结点的添加位置
            Node node = subtreeSearch(root, v);
            boolean isAddLeft = v <= node.val; // 是否将新结点添加到node的左子结点
            if (node.val == v) { // 如果值为v的结点已存在
                if (node.left != null) { // 值为v的结点存在左子结点，则添加到其左子树的最右侧
                    node = subtreeLast(node.left);
                    isAddLeft = false;
                } else { // 值为v的结点不存在左子结点，则添加到其左子结点
                    isAddLeft = true;
                }
            }

            // 添加新结点
            Node leaf = new Node(v, node);
            if (isAddLeft) {
                node.left = leaf;
            } else {
                node.right = leaf;
            }

            rebalance(leaf);
        }
    }

    // 删除值为v的结点 -> 返回是否成功删除结点
    public boolean delete(int v) {
        if (root == null) {
            return false;
        }

        Node node = subtreeSearch(root, v);
        if (node.val != v) { // 没有找到需要删除的结点
            return false;
        }

        // 处理当前结点既有左子树也有右子树的情况
        // 若左子树比右子树高度低，则将当前结点替换为右子树最左侧的结点，并移除右子树最左侧的结点
        // 若右子树比左子树高度低，则将当前结点替换为左子树最右侧的结点，并移除左子树最右侧的结点
        if (node.left != null && node.right != null) {
            Node replacement = null;
            if (node.left.height <= node.right.height) {
                replacement = subtreeFirst(node.right);
            } else {
                replacement = subtreeLast(node.left);
            }
            node.val = replacement.val;
            node = replacement;
        }

        Node parent = node.parent;
        delete(node);
        rebalance(parent);
        return true;
    }

    // 删除结点p并用它的子结点代替它，结点p至多只能有1个子结点
    private void delete(Node node) {
        if (node.left != null && node.right != null) {
            return;
            // throw new Exception("Node has two children");
        }
        Node child = node.left != null ? node.left : node.right;
        if (child != null) {
            child.parent = node.parent;
        }
        if (node == root) {
            root = child;
        } else {
            Node parent = node.parent;
            if (node == parent.left) {
                parent.left = child;
            } else {
                parent.right = child;
            }
        }
        node.parent = node;
    }

    // 在以node为根结点的子树中搜索值为v的结点，如果没有值为v的结点，则返回值为v的结点应该在的位置的父结点
    private Node subtreeSearch(Node node, int v) {
        if (node.val < v && node.right != null) {
            return subtreeSearch(node.right, v);
        } else if (node.val > v && node.left != null) {
            return subtreeSearch(node.left, v);
        } else {
            return node;
        }
    }

    // 重新计算node结点的高度和元素数
    private void recompute(Node node) {
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        node.size = 1 + getSize(node.left) + getSize(node.right);
    }

    // 从node结点开始（含node结点）逐个向上重新平衡二叉树，并更新结点高度和元素数
    private void rebalance(Node node) {
        while (node != null) {
            int oldHeight = node.height, oldSize = node.size;
            if (!isBalanced(node)) {
                node = restructure(tallGrandchild(node));
                recompute(node.left);
                recompute(node.right);
            }
            recompute(node);
            if (node.height == oldHeight && node.size == oldSize) {
                node = null; // 如果结点高度和元素数都没有变化则不需要再继续向上调整
            } else {
                node = node.parent;
            }
        }
    }

    // 判断node结点是否平衡
    private boolean isBalanced(Node node) {
        return Math.abs(getHeight(node.left) - getHeight(node.right)) <= 1;
    }

    // 获取node结点更高的子树
    private Node tallChild(Node node) {
        if (getHeight(node.left) > getHeight(node.right)) {
            return node.left;
        } else {
            return node.right;
        }
    }

    // 获取node结点更高的子树中的更高的子树
    private Node tallGrandchild(Node node) {
        Node child = tallChild(node);
        return tallChild(child);
    }

    // 重新连接父结点和子结点（子结点允许为空）
    private static void relink(Node parent, Node child, boolean isLeft) {
        if (isLeft) {
            parent.left = child;
        } else {
            parent.right = child;
        }
        if (child != null) {
            child.parent = parent;
        }
    }

    // 旋转操作
    private void rotate(Node node) {
        Node parent = node.parent;
        Node grandparent = parent.parent;
        if (grandparent == null) {
            root = node;
            node.parent = null;
        } else {
            relink(grandparent, node, parent == grandparent.left);
        }

        if (node == parent.left) {
            relink(parent, node.right, true);
            relink(node, parent, false);
        } else {
            relink(parent, node.left, false);
            relink(node, parent, true);
        }
    }

    // trinode操作
    private Node restructure(Node node) {
        Node parent = node.parent;
        Node grandparent = parent.parent;

        if ((node == parent.right) == (parent == grandparent.right)) { // 处理需要一次旋转的情况
            rotate(parent);
            return parent;
        } else { // 处理需要两次旋转的情况：第1次旋转后即成为需要一次旋转的情况
            rotate(node);
            rotate(node);
            return node;
        }
    }

    // 返回以node为根结点的子树的第1个元素
    private static Node subtreeFirst(Node node) {
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }

    // 返回以node为根结点的子树的最后1个元素
    private static Node subtreeLast(Node node) {
        while (node.right != null) {
            node = node.right;
        }
        return node;
    }

    // 获取以node为根结点的子树的高度
    private static int getHeight(Node node) {
        return node != null ? node.height : 0;
    }

    // 获取以node为根结点的子树的结点数
    private static int getSize(Node node) {
        return node != null ? node.size : 0;
    }
}