聚类算法的性能度量
聚类算法就是根据数据中样本与样本之间的距离或相似度,将样本划分为若干组/类/簇,其划分的原则:簇内样本相似、簇间样本不相似,聚类的结果是产生一个簇的集合。
其划分方式主要分为两种,
- 嵌套类型

- 非嵌套类型
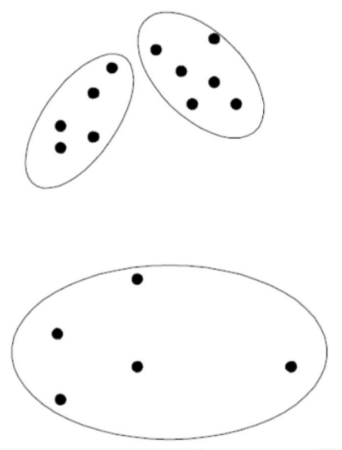
其中簇往往分为三种情况
- 基于中心的簇:簇内的点和其“中心”较为相近(或相似),和其他簇的“中心”较远,这样的一组样本形成的簇
- 基于邻接的簇:相比其他任何簇的点,每个点都至少和所属簇的某一个点更近
- 基于密度的簇:簇是由高密度的区域形成的,簇之间是一些低密度的区域
簇的相似性与距离度量
若采用距离为度量
闵可夫斯基距离:
d
i
s
t
(
x
i
,
x
j
)
=
(
∑
d
=
1
D
∣
x
i
,
d
−
x
j
,
d
∣
p
)
1
/
p
dist(x^i,x^j)=\left(\sum_{d=1}^D|x_{i,d}-x_{j,d}|^p\right)^{1/p}
dist(xi,xj)=(∑d=1D∣xi,d−xj,d∣p)1/p
当
p
=
2
p=2
p=2时,为欧氏距离
:
d
i
s
t
(
x
i
,
x
j
)
=
∑
d
=
1
D
(
x
i
,
d
−
x
j
,
d
)
2
:dist(x^i,x^j)=\sqrt{\sum_{d=1}^D\left(x_{i,d}-x_{j,d}\right)^2}
:dist(xi,xj)=∑d=1D(xi,d−xj,d)2
当
p
=
1
p=1
p=1时,为曼哈顿距离:
d
i
s
t
(
x
i
,
x
j
)
=
∑
d
=
1
D
∣
x
i
,
d
−
x
j
,
d
∣
dist(x^i,x^j)=\sum_{d=1}^D\left|x_{i,d}-x_{j,d}\right|
dist(xi,xj)=∑d=1D∣xi,d−xj,d∣
这类距离函数对特征的旋转和平移变换不敏感,对数值尺度敏感
若采用余弦相似度量
两变量
x
i
,
x
j
x^i,x^j
xi,xj,看作D维空间的两个向量,这两个向量间的夹角余弦可用下式进行计算
s
(
x
i
,
x
j
)
=
∑
d
=
1
D
x
i
,
d
x
j
,
d
∑
d
=
1
D
x
i
,
d
2
∑
d
=
1
D
x
j
,
d
2
=
(
x
i
)
T
x
j
∥
x
i
∥
∥
x
j
∥
s(x^i,x^j)=\frac{\sum_{d=1}^Dx_{i,d}x_{j,d}}{\sqrt{\sum_{d=1}^Dx_{i,d}^2}\sqrt{\sum_{d=1}^Dx_{j,d}^2}}=\frac{(x^i)^Tx^j}{\|x^i\|\|x^j\|}
s(xi,xj)=∑d=1Dxi,d2∑d=1Dxj,d2∑d=1Dxi,dxj,d=∥xi∥∥xj∥(xi)Txj
若采用相关系数
r
(
x
i
,
x
j
)
=
c
o
v
(
x
i
,
x
j
)
σ
x
i
σ
x
j
=
E
[
(
x
i
−
μ
i
)
(
x
j
−
μ
j
)
]
σ
x
i
σ
x
j
=
∑
d
=
1
D
(
x
i
,
d
−
μ
i
,
d
)
(
x
j
,
d
−
μ
j
,
d
)
∑
d
=
1
D
(
x
i
,
d
−
μ
i
,
d
)
2
∑
d
=
1
D
(
x
j
,
d
−
μ
j
,
d
)
2
\begin{gathered} r(x^i,x^j)=\frac{cov(x^i,x^j)}{\sigma_{x_i}\sigma_{x_j}}=\frac{\mathbb{E}[(x^i-\mu^i)(x^j-\mu^j)]}{\sigma_{x_i}\sigma_{x_j}} \\ \begin{aligned}=\frac{\sum_{d=1}^D(x_{i,d}-\mu_{i,d})(x_{j,d}-\mu_{j,d})}{\sqrt{\sum_{d=1}^D\left(x_{i,d}-\mu_{i,d}\right)^2\sum_{d=1}^D\left(x_{j,d}-\mu_{j,d}\right)^2}}\end{aligned} \end{gathered}
r(xi,xj)=σxiσxjcov(xi,xj)=σxiσxjE[(xi−μi)(xj−μj)]=∑d=1D(xi,d−μi,d)2∑d=1D(xj,d−μj,d)2∑d=1D(xi,d−μi,d)(xj,d−μj,d)
当数据采用中心化处理后
μ
i
=
μ
j
=
0
\mu_i=\mu_j=0
μi=μj=0,相关系数等于余弦相似度
对聚类算法的性能评价指标
参考模型
设存在数据集 D = { x 1 , x 2 , . . . x N } D=\{x^1,x^2,...x^N\} D={x1,x2,...xN},聚类结果 : C = { C 1 , C 2 , . . . C K } :C=\{\mathcal{C}_1,\mathcal{C}_2,...\mathcal{C}_K\} :C={C1,C2,...CK},其中 C k \mathcal{C}_k Ck表示属于类别 k k k的样本的集合,其中参考模型的分类结果为 C ∗ = { C 1 ∗ , . . . , C K ∗ } \mathcal{C}^*=\{\mathcal{C}_1^*,...,\mathcal{C}_K^*\} C∗={C1∗,...,CK∗}, λ \lambda λ 和 λ ∗ \lambda^* λ∗ 分别为 c c c和 c ∗ c^* c∗ 的标记向量
其中聚类结果有4种情况
a
=
{
(
x
i
,
x
j
)
∣
x
i
,
x
j
∈
C
k
;
x
i
,
x
j
∈
C
l
∗
}
在两种聚类结果中,两个样本的所属的簇相同
d
=
{
(
x
i
,
x
j
)
∣
x
i
∈
C
k
1
,
x
j
∈
C
k
2
;
x
i
∈
C
l
1
∗
,
x
j
∈
C
l
2
∗
}
在两种聚类结果中,两个样本的所属的簇不同
b
=
{
(
x
i
,
x
j
)
∣
x
i
,
x
j
∈
C
k
;
x
i
∈
C
l
1
∗
,
x
j
∈
C
l
2
∗
}
c
=
{
(
x
i
,
x
j
)
∣
x
i
∈
C
k
1
,
x
j
∈
C
k
2
;
x
i
,
x
j
∈
C
l
∗
}
\begin{aligned} a=&\begin{Bmatrix}(x^i,x^j)|x^i,x^j\in\mathcal{C}_k;&x^i,x^j\in\mathcal{C}_l^*\end{Bmatrix}\\ &\text{在两种聚类结果中,两个样本的所属的簇相同}\\ d=&\{(x^i,x^j)|x^i\in\mathcal{C}_{k1},x^j\in\mathcal{C}_{k2};\:x^i\in\mathcal{C}_{l1}^*,x^j\in\mathcal{C}_{l2}^*\}\\ &\text{在两种聚类结果中,两个样本的所属的簇不同}\\ b=&\big\{(x^i,x^j)|x^i,x^j\in\mathcal{C}_k;\:x^i\in C_{l1}^*,x^j\in\mathcal{C}_{l2}^*\big\}\\ c=&\big\{(x^i,x^j)|x^i\in\mathcal{C}_{k1},x^j\in\mathcal{C}_{k2};\:x^i,x^j\in\mathcal{C}_l^*\big\} \end{aligned}
a=d=b=c={(xi,xj)∣xi,xj∈Ck;xi,xj∈Cl∗}在两种聚类结果中,两个样本的所属的簇相同{(xi,xj)∣xi∈Ck1,xj∈Ck2;xi∈Cl1∗,xj∈Cl2∗}在两种聚类结果中,两个样本的所属的簇不同{(xi,xj)∣xi,xj∈Ck;xi∈Cl1∗,xj∈Cl2∗}{(xi,xj)∣xi∈Ck1,xj∈Ck2;xi,xj∈Cl∗}
每个样本对
(
x
i
,
x
j
)
(
i
<
j
)
(x_i,x_j)(i<j)
(xi,xj)(i<j) 仅能出现在一个集合中,因此有
a
+
b
+
c
+
d
=
m
(
m
−
1
)
/
2
a+b+c+d=m(m-1)/2
a+b+c+d=m(m−1)/2 成立

Jaccard 系数(Jaccard Coefficient, 简称 JC)
JC
=
a
a
+
b
+
c
\text{JC}=\frac a{a+b+c}
JC=a+b+ca
FM 指数(Fowlkes and Mallows Index, 简称 FMI)
F
M
I
=
a
a
+
b
⋅
a
a
+
c
\mathrm{FMI}=\sqrt{\frac a{a+b}\cdot\frac a{a+c}}
FMI=a+ba⋅a+ca
Rand 指数(Rand Index, 简称 RI$) $
R
I
=
2
(
a
+
d
)
N
(
N
−
1
)
\mathrm{RI}=\frac{2(a+d)}{N(N-1)}
RI=N(N−1)2(a+d)
上述性能度量的结果值均在 [0,1] 区间,值越大越好
无参考模型
其要求簇内相似度越大越好,簇间相似度越小越好
平均距离:
a
v
g
(
C
k
)
=
1
∣
C
k
∣
(
∣
C
k
∣
−
1
)
∑
x
i
,
x
j
∈
C
k
d
i
s
t
(
x
i
,
x
j
)
avg(\mathcal{C}_k)=\frac1{|\mathcal{C}_k|(|\mathcal{C}_k|-1)}\sum_{x^i,x^j\in\mathcal{C}_k}dist(x^i,x^j)
avg(Ck)=∣Ck∣(∣Ck∣−1)1xi,xj∈Ck∑dist(xi,xj)
最大距离:
d
i
a
m
(
C
k
)
=
max
x
i
,
x
j
∈
C
k
d
i
s
t
(
x
i
,
x
j
)
diam\left(\mathcal{C}_k\right)=\max_{x^i,x^j\in\mathcal{C}_k}dist(\boldsymbol{x}^i,\boldsymbol{x}^j)
diam(Ck)=xi,xj∈Ckmaxdist(xi,xj)
簇的半径:
d
i
a
m
(
C
k
)
=
1
∣
C
k
∣
∑
x
i
∈
C
k
(
d
i
s
t
(
x
i
,
μ
k
)
)
2
diam(\mathcal{C}_k)=\sqrt{\frac1{|C_k|}\sum_{x^i\in\mathcal{C}_k}(dist(x^i,\mu^k))^2}
diam(Ck)=∣Ck∣1xi∈Ck∑(dist(xi,μk))2
其中
μ
k
=
1
∣
C
k
∣
∑
x
i
∈
C
k
x
i
\mu^{k}=\frac{1}{|\mathcal{C}_{k}|}\sum_{x^{i}\in\mathcal{C}_{k}}\boldsymbol{x}^{i}
μk=∣Ck∣1∑xi∈Ckxi
最小距离:
d
m
i
n
(
C
k
,
C
l
)
=
min
x
i
∈
C
k
,
x
j
∈
C
l
d
i
s
t
(
x
i
,
x
j
)
d_{min}(\mathcal{C}_k,\mathcal{C}_l)=\min_{x^i\in\mathcal{C}_k,x^j\in\mathcal{C}_l}dist(x^i,x^j)
dmin(Ck,Cl)=xi∈Ck,xj∈Clmindist(xi,xj)
类中心的距离:
d
c
e
n
(
C
k
,
C
l
)
=
d
i
s
t
(
μ
k
,
μ
l
)
,
d_{cen}(\mathcal{C}_k,\mathcal{C}_l)=dist(\mathbf{\mu}^k,\mathbf{\mu}^l),
dcen(Ck,Cl)=dist(μk,μl),
DB指数(DBI)【簇内距离/簇间距离】:
D
B
I
=
1
K
∑
k
=
1
K
max
k
≠
l
arg
(
C
k
)
+
a
v
g
(
C
l
)
d
c
e
n
(
C
k
,
C
l
)
DBI=\frac1K\sum_{k=1}^K\max_{k\neq l}\frac{\arg(\mathcal{C}_k)+avg(\mathcal{C}_l)}{d_{cen}(\mathcal{C}_k,\mathcal{C}_l)}
DBI=K1k=1∑Kk=lmaxdcen(Ck,Cl)arg(Ck)+avg(Cl)
其中DBI越小越好,即簇越小越远
Dunn 指数(DI)【最小簇间距离/最大簇的半径】:
D
I
=
min
1
≤
k
<
l
≤
K
d
m
i
n
(
C
k
,
C
l
)
max
1
≤
k
≤
K
d
i
a
m
(
C
k
)
DI=\min_{1\leq k<l\leq K}\frac{d_{min}(\mathcal{C}_k,\mathcal{C}_l)}{\max_{1\leq k\leq K}diam(\mathcal{C}_k)}
DI=1≤k<l≤Kminmax1≤k≤Kdiam(Ck)dmin(Ck,Cl)
其中DI越大越好