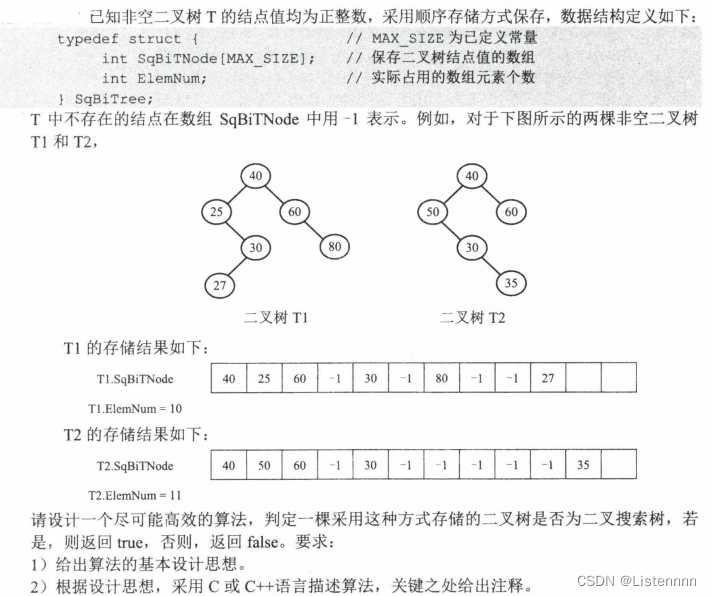
- 对于采用顺序存储方式保存的二叉树,根结点保存在SqBiTNode[0]中;当某结点保存SqBiTNode[i]中时,若有左孩子,则其值保存在SqBiTNode [2i+1]中;若有右孩子,则其值保存在SqBiTNode[2i+2]中;若有双亲结点,则其值保存在SqBiTNode [(i-1)/2]中
- 二叉搜索树需要满足的条件是:任一结点值大于其左子树中的全部结点值,小于其右子树中的全部结点值。中序遍历二叉搜索树得到一个升序序列
算法思想
- 对二叉树进行中序遍历,在遍历过程中,判断当前访问结点是否大于等于上一个访问的结点,若遍历的每个结点均满足条件,则遍历结束后返回true,否则返回false
算法实现
int preIndex = 0;
bool isBST(SqBiTree *T,int index){
if(T->SqBiNode[index] == -1) return true;
if(!isBST(T,index*2+1)) return false;
if(T->SqBiNode[index] <= T->SqBiNode[preIndex]) return false;
else preIndex = index;
if(!isBST(T,index*2+2)) return false;
return true;
}
补充:链式存储的二叉树判断是否为二叉排序树
- 二叉排序的中序遍历时递增有序的序列
- 设置全局变量temp记录已访问过结点的最大值
- 设置全局变量flag记录是否满足后访问的结点始终大于先前访问的结点
- 若遍历结束后,flag的值未发生变化,为true,则是二叉排序树
int temp=MIN_INT;
bool isBST=true;
void InOrder(BiTree T){
if(T =NULL)return;
InOrder(T->Ichild);
if (T->data >temp){
temp=T->data;
else
isBST=false;
InOrder(T->rchild);
}
TreeNode* pre = NULL;
bool isValidBST(TreeNode* root) {
if (root == NULL) return true;
bool left = isValidBST(root->left);
if (pre != NULL && pre->val >= root->val) return false;
pre = root;
bool right = isValidBST(root->right);
return left && right;
}