数字逻辑电路基础-组合逻辑电路之4位先行进位加法器

news2024/11/17 2:46:09

文章目录

    • 一、问题描述
    • 二、verilog源码
    • 三、仿真结果

一、问题描述

前面介绍4位行波进位全加器（串行加法器）的原理及verilog实现，但是它是一种串行加法器，当位数多时，比如32位的二进制数相加，由于进位逐位从低位向高位传递，这会造成相当大的延迟。对于需要快速加法运算的信号处理电路来说，我们需要对其进行改进，一个常见的想法就是将进位提前计算出来，这样我们可以实现一种称为超前进位加法器的加法电路。

4位超前进位加法器的结构如下图所示：
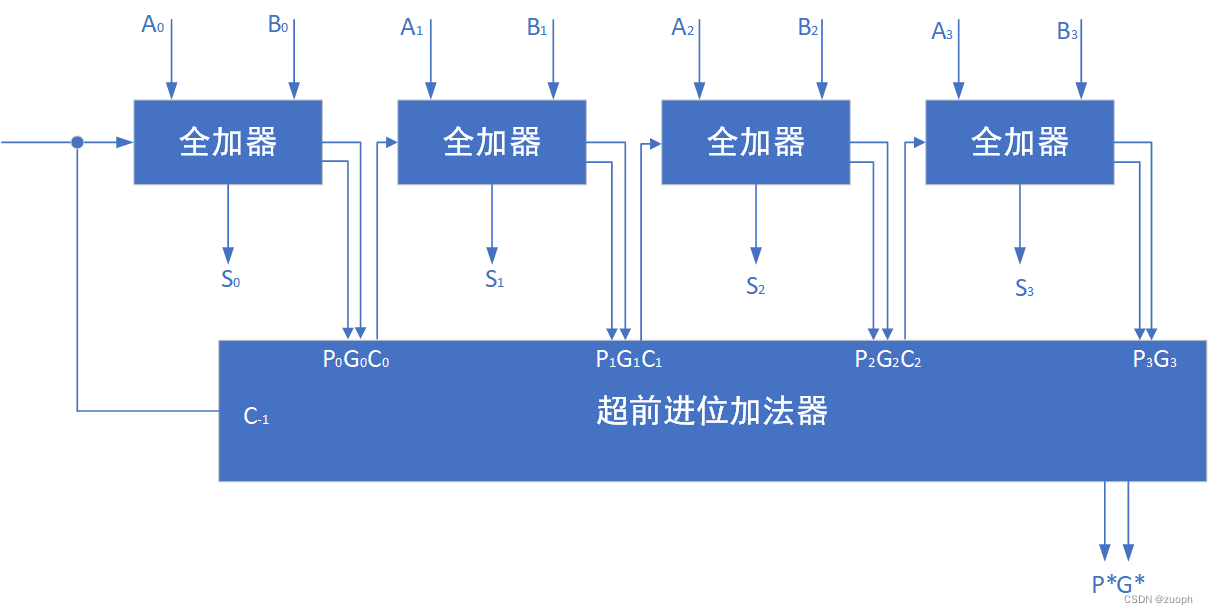
4位超前进位加法器

其中
Pi=Ai or Bi 称为进位传递函数
Gi=Ai and Bi 称为进位产生函数

Si=Pi xor Ci
Ci=(Pi and Ci-1) or Gi

根据上述逻辑等式算出各进位的逻辑值：
C0 = cin
C1=G0 + P0·C0
C2=G1 + P1·C1 = G1 + P1·G0 + P1·P0 ▪C0
C3=G2 + P2·C2 = G2 + P2·G1 + P2·P1·G0 + P2·P1·P0·C0
C4=G3 + P3·C3 = G3 + P3·G2 + P3·P2·G1 + P3·P2·P1·G0 + P3·P2·P1·P0·C0
cout=C4

二、verilog源码

module cla_adder4b(
  input[3:0] a,
  input[3:0] b,
  input cin,
  output[3:

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1299131.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

LeNet

LeNet

概念 代码 model import torch.nn as nn import torch.nn.functional as Fclass LeNet(nn.Module):def __init__(self):super(LeNet, self).__init__() # super()继承父类的构造函数self.conv1 nn.Conv2d(3, 16, 5)self.pool1 nn.MaxPool2d(2, 2)self.conv2 nn.Conv2d(16…
阅读更多...
Three.js+pcl.js 实现Web端的点云处理+显示

Three.js+pcl.js 实现Web端的点云处理+显示

1 功能实现 在前面我们实现了PCD的加载器的基础上，这次将加上 pcl.js —— 著名的PCL库的web版本，详情见https://pcl.js.org/，来处理我们加载上去的点云。 具体实现如下： 用户可以通过每个板块的右上角进行处理前 / 后的切换&am…
阅读更多...
php使用vue.js实现省市区三级联动

php使用vue.js实现省市区三级联动

参考gpt 有问题问gpt 实现效果 现省市区三级联动的方法可以使用PHP结合AJAX异步请求来实现。下面是一个简单的示例代码&#xff1a; HTML部分&#xff1a; <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>省市区三级联动…
阅读更多...
vue-seamless-scroll无缝滚动组件

vue-seamless-scroll无缝滚动组件

首先找到他的官网vue-seamless-scroll 1.进行安装依赖 vue2 npm install vue-seamless-scroll --save vue3 npm install vue3-seamless-scroll --save 2.全局引入 vue2 import scroll from vue-seamless-scroll Vue.use(scroll) vue3 import vue3SeamlessScroll fro…
阅读更多...
JVM 内存分析工具 Memory Analyzer Tool（MAT）的深度讲解

JVM 内存分析工具 Memory Analyzer Tool（MAT）的深度讲解

目录 一. 前言 二. MAT 使用场景及主要解决问题 三. MAT 基础概念 3.1. Heap Dump 3.2. Shallow Heap 3.3. Retained Set 3.4. Retained Heap 3.5. Dominator Tree 3.6. OQL 3.7. references 四. MAT 功能概述 4.1. 内存分布 4.2. 对象间依赖 4.3. 对象状态 4.4…
阅读更多...
【交流】PHP生成唯一邀请码

【交流】PHP生成唯一邀请码

目录 前言&#xff1a; 1.随机生成&#xff0c;核对user表是否已存在 代码&#xff1a; 解析&#xff1a; 缺点&#xff1a; 2.建表建库&#xff0c;每次从表中随机抽取一条&#xff0c;用完时扩充 表结构 表视图 代码 解析 缺点 结论&#xff1a; 前言&#xff1a; …
阅读更多...
【rabbitMQ】rabbitMQ的下载，安装与配置

【rabbitMQ】rabbitMQ的下载，安装与配置

目录 1. 下载Erland 安装步骤&#xff1a; 配置环境变量&#xff1a; 校验环境变量配置是否成功 2.下载MQ 安装步骤&#xff1a; 添加可视化插件 &#xff1a; 启动&#xff1a; 拒绝访问 1. 下载Erland 因为rabbitMQ是基于Erland,所以在安装rabbitMQ之前需要安装Erla…
阅读更多...
距离度量（各距离含义）

距离度量（各距离含义）

欧氏距离 在n维空间中两点的真实距离&#xff0c;向量的自然长度 由于欧几里得几何学的关系称为欧氏距离 二维空间两点计算公式&#xff1a; d ( x 1 − x 2 ) 2 ( y 1 − y 2 ) 2 d \sqrt{(x_1 - x_2)^2 (y_1 - y_2)^2} d(x1​−x2​)2(y1​−y2​)2 ​ 三维空间两点计算…
阅读更多...
7.MySQL 存储过程

7.MySQL 存储过程

目录 概述 概念&#xff1a; 特性&#xff1a; 变量 局部变量 定义方法&#xff1a; 语法1: 语法2: 用户变量 语法&#xff1a; 系统变量 全局变量 会话变量 参数传递 in out inout 流程控制 分支语句 if case 循环语句 循环控制: while while while…
阅读更多...
Java面试遇到的一些常见题

Java面试遇到的一些常见题

目录 1. Java语言有几种基本类型&#xff0c;分别是什么&#xff1f; 整数类型&#xff08;Integer Types&#xff09;&#xff1a; 浮点类型&#xff08;Floating-Point Types&#xff09;&#xff1a; 字符类型&#xff08;Character Type&#xff09;&#xff1a; 布尔类…
阅读更多...
基于Springboot的校园失物招领系统（有报告）。Javaee项目，springboot项目。

基于Springboot的校园失物招领系统（有报告）。Javaee项目，springboot项目。

演示视频&#xff1a; 基于Springboot的校园失物招领系统&#xff08;有报告&#xff09;。Javaee项目&#xff0c;springboot项目。 项目介绍&#xff1a; 采用M&#xff08;model&#xff09;V&#xff08;view&#xff09;C&#xff08;controller&#xff09;三层体系结构…
阅读更多...
【智能家居】七、人脸识别 翔云平台编程使用(编译openSSL支持libcurl的https访问、安装SSL依赖库openSSL)

【智能家居】七、人脸识别 翔云平台编程使用(编译openSSL支持libcurl的https访问、安装SSL依赖库openSSL)

一、翔云 人工智能开放平台 API文档开发示例下载 二、编译openSSL支持libcurl的https访问 安装SSL依赖库openSSL(使用工具wget)libcurl库重新配置&#xff0c;编译&#xff0c;安装运行&#xff08;运行需添加动态库为环境变量&#xff09; 三、编程实现人脸识别 四、Base6…
阅读更多...
react中使用react-konva实现画板框选内容

react中使用react-konva实现画板框选内容

文章目录 一、前言1.1、API文档1.2、Github仓库 二、图形2.1、拖拽draggable2.2、图片Image2.3、变形Transformer 三、实现3.1、依赖3.2、源码3.2.1、KonvaContainer组件3.2.2、use-key-press文件 3.3、效果图 四、最后 一、前言 本文用到的react-konva是基于react封装的图形绘…
阅读更多...
【rabbitMQ】rabbitMQ控制台模拟收发消息

【rabbitMQ】rabbitMQ控制台模拟收发消息

目录 1.新建队列 2.交换机绑定队列 3.查看消息是否到达队列 总结&#xff1a; 1.新建队列 2.交换机绑定队列 点击amq.fonout 3.查看消息是否到达队列 总结&#xff1a; 生产者&#xff08;publisher&#xff09;发送消息&#xff0c;先到达交换机&#xff0c;再到队列&…
阅读更多...
深度学习之全面了解预训练模型

深度学习之全面了解预训练模型

在本专栏中&#xff0c;我们将讨论预训练模型。有很多模型可供选择&#xff0c;因此也有很多考虑事项。 这次的专栏与以往稍有不同。我要回答的问题全部源于 MathWorks 社区论坛&#xff08;ww2.mathworks.cn/matlabcentral/&#xff09;的问题。我会首先总结 MATLAB Answers …
阅读更多...
计算机视觉-05-目标检测：LeNet的PyTorch复现（MNIST手写数据集篇）（包含数据和代码）

计算机视觉-05-目标检测：LeNet的PyTorch复现（MNIST手写数据集篇）（包含数据和代码）

文章目录 0. 数据下载1. 背景描述2. 预测目的3. 数据总览4. 数据预处理4.1 下载并加载数据&#xff0c;并做出一定的预先处理4.2 搭建 LeNet-5 神经网络结构&#xff0c;并定义前向传播的过程4.3 将定义好的网络结构搭载到 GPU/CPU&#xff0c;并定义优化器4.4 定义训练过程4.5…
阅读更多...
机器学习算法（9）——集成技术（Bagging——随机森林分类器和回归）

机器学习算法（9）——集成技术（Bagging——随机森林分类器和回归）

一、说明 在这篇文章&#xff0c;我将向您解释集成技术和著名的集成技术之一&#xff0c;它属于装袋技术&#xff0c;称为随机森林分类器和回归。 集成技术是机器学习技术&#xff0c;它结合多个基本模块和模型来创建最佳预测模型。为了更好地理解这个定义&#xff0c;我们需要…
阅读更多...
C语言进阶之路之结构体、枚举关卡篇

C语言进阶之路之结构体、枚举关卡篇

目录 一、学习目标 二、组合数据类型-结构体 结构体基本概念 结构体的声明&#xff1a; 小怪实战 结构体初始化 指定成员初始化的好处&#xff1a; 结构体成员引用 结构体指针与数组 关卡BOOS 三、结构体的尺寸 CPU字长 地址对齐 结构体的M值 可移植性 四、联合体…
阅读更多...
ssm的健身房预约系统（有报告）。Javaee项目。ssm项目。

ssm的健身房预约系统（有报告）。Javaee项目。ssm项目。

演示视频&#xff1a; ssm的健身房预约系统&#xff08;有报告&#xff09;。Javaee项目。ssm项目。 项目介绍&#xff1a; 采用M&#xff08;model&#xff09;V&#xff08;view&#xff09;C&#xff08;controller&#xff09;三层体系结构&#xff0c;通过Spring Spring…
阅读更多...
极智一周 | AI 算力国产化、通义开源、Gemini、鸿蒙、蔚来 And so on

极智一周 | AI 算力国产化、通义开源、Gemini、鸿蒙、蔚来 And so on

欢迎关注我的公众号 [极智视界]&#xff0c;获取我的更多技术分享 大家好&#xff0c;我是极智视界&#xff0c;带来本周的 [极智一周]&#xff0c;关键词&#xff1a;AI 算力国产化、通义开源、Gemini、鸿蒙、蔚来 And so on。 邀您加入我的知识星球「极智视界」&#xff0c;…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023