题目描述

给出一个数 $n$ 以及 $x$ , $y$ , $z$ ，求 $1$ 到 $n$ 中，有多少个数不是 $x$, $y$, $z$ 中任意一个数的倍数。

输入格式

第一行输入一个整数 $T$，表示测试组数（ $1\le T\le 10^5$ ）.

接下来会有 $T$ 行输入，每行 $4$ 个整数 $n$, $x$, $y$, $z$（$1\le n\le 10^{18}$, $1\le x,y,z\le 10^6$ ）.

输出格式

共 $T$ 行，每行输出一个整数，表示 $1$ 到 $n$ 中，不是 $x$, $y$, $z$ 中任意一个数倍数的整数个数。

测试样例

2
10 3 4 5
100 2 4 6

3
50

温馨提示

递归求解int范围内两数的最大公约数的代码模板如下。

// C/C++ code
int gcd(int a, int b) {
    return b == 0 ? a : gcd(b, a % b);
}

// Java code
public int gcd(int a, int b){
    return b == 0 ? a : gcd(b, a % b);
}

# Python code
def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

Idea from HGG.

思路

直接求“不是”的个数比较难求，但是我们这里可以转化成求“是x、y、z中任意一个数的倍数”的个数，那么现在就是一个容斥问题

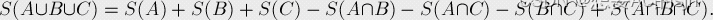
注意个数的取值范围，求个数的时候向下取整

核心代码

#include <iostream>
using namespace std;

inline long long gcd(long long a,long long b) 
{    
    if(b) while((a%=b) && (b%=a));    
    return a+b;
}

void solve()
{
	long long n,x,y,z;
	scanf("%lld%lld%lld%lld",&n,&x,&y,&z);
	long long a=x/gcd(x,y)*y;
	long long b=x/gcd(x,z)*z;
	long long c=y/gcd(y,z)*z;
	long long d=a/gcd(a,z)*z;
//	cout<<a<<"\n"<<b<<"\n"<<c<<"\n"<<d<<"\n"; 
	cout<<n-n/x-n/y-n/z+n/a+n/b+n/c-n/d<<"\n";
}

int main() {
	int t=1;
	cin>>t;
	while(t--)
	{
		solve();
	}
	return 0;
}