Problem: 37. 解数独

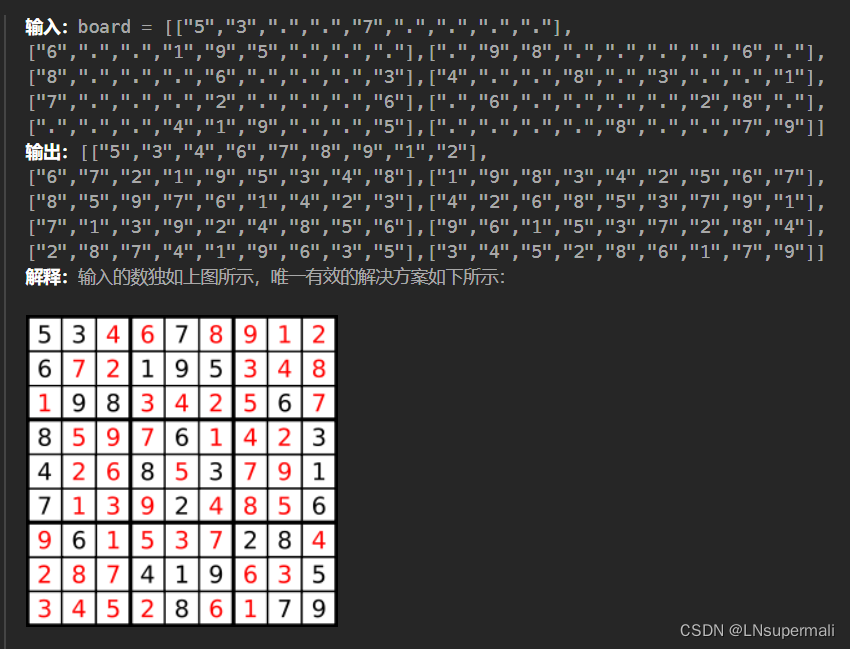
题目描述

思路

该题可以使用回溯来模拟穷举。回溯问题通常涉及到可选列表，决策阶段，决策路径，而对于本题目我们选择将棋盘的每一个格子作为决策阶段，为此我们应该解决如何判断当前棋盘格子位置处是否可以放置1~9中的一个数字，为此我们可以：

1.若当前棋盘格子位置处已经存在数字，则直接递归下一个格子，但是当此时的格子属于棋盘的边缘时，要注意换行，当决策阶段等于9时说明已经找到一个解；
2.当当前棋盘格子位置处为空格，判断当前位置可填的数字将其填写到当前格子，并递归下一个格子（若格子为棋盘边缘，处理同上），最后将当前的格子复原！
3.我们可以定义三个boolean类型的的数组:

3.1boolean[][] rows = new boolean[9][10];用于辅助记录棋盘某一行上存在1-9中的某个数字，例如rows[2][2]表示棋盘第二行存在数字2；
3.2boolean[][] cols = new boolean[9][10];用于辅助记录棋盘某一列上存在1-9中的某个数字，例如cols[2][2]表示棋盘第二列存在数字2；
3.3boolean[][][] blocks = new boolean[3][3][10];用于辅助记录9x9棋盘某一个3x3的小矩形区间是否存在1-9中的某个数字，例如blocks[1][1][1]表示以3x3的小矩形为一个小数组（假设可以看作一个小数组）的大的二维数组中的第一行第一列中存在数字1。进一步我们容易得到若实际的棋盘中的一个格子的小标为（i，j）则对应到blocks中为（i/3,j/3）;

解题方法

1.定义如思路中的三个boolean类性的辅助数组，并定义一个全局变量solved初始化为false，用于记录是否已经找到了一个解（因为题目只需要找到一个解即可）
2.将棋盘中本存在的数字填入棋盘，并将三个辅助数组对应位置设置为true（表示该行、该列、该3x3区域已经存在某个数字）
3.回溯函数：由参数row（棋盘当前行）与col（棋盘当前列）共同确定决策阶段

3.1当row == 9时表示已经找到一组解，则将solved置为true并返回；
3.2若当前格子已经存在数字则找处当前格子的下一个格子（也就是当前决策阶段的下一个决策阶段）若col不等于8（由于棋盘是9x9的棋盘则棋盘边缘位置的col等于8）时，直接右移动一个位置，否则直接换到下一行，并直递归处理下一决策阶段，若此时solved已经为true则直接返回即可。
3.3若当前格子为空格则利用for循环并结合三个辅助数组判断并将合适的数填写到当前格子，并同上处理下一个格子，同理若solved为true则直接返回，最后将当前格子（决策阶段）复原！！！

复杂度

时间复杂度:

最坏时间复杂度, $O(n^{n^2})$其中n为棋盘的大小

空间复杂度:

$O(n^2)$其中n为棋盘的大小

Code

class Solution {
    //Array used to aid judgment
    private boolean[][] rows = new boolean[9][10];
    private boolean[][] cols = new boolean[9][10];
    private boolean[][][] blocks = new boolean[3][3][10];
    //Judgment for early exit recursion
    private boolean solved = false;

    /**
     *
     * @param board
     */
    public void solveSudoku(char[][] board) {
        //Initializes the data in the chessboard
        for (int i = 0; i < 9; ++i) {
            for (int j = 0; j < 9; ++j) {
                if (board[i][j] != '.') {
                    int num = board[i][j] - '0';
                    //Set to true in the array used for auxiliary judgment
                    rows[i][num] = true;
                    cols[j][num] = true;
                    blocks[i/3][j/3][num] = true;
                }
            }
        }
        backtrack(0, 0, board);
    }

    private void backtrack(int row, int col, char[][] board) {
        //End condition
        if (row == 9) {
            solved = true;
            return;
        }
        /*
        Process each cell on the board (the backtracking decision stage)
         by moving directly to the next cell in the same row
         if it is on the same row and not on the edge of the board,
         otherwise wrap the line
         */
        if (board[row][col] != '.') {
            int nextRow = row;
            int nextCol = col + 1;
            //On the edge
            if (col == 8) {
                //wrap the line
                nextRow = row + 1;
                nextCol = 0;
            }
            //Recursive next stage
            //The current cell has been filled with numbers
            backtrack(nextRow, nextCol,board);
            //Found a solution. Exit the recursion early
            if (solved) {
                return;
            }
        } else {
            for (int num = 1; num <= 9; ++num) {
                if (!rows[row][num] && !cols[col][num] && !blocks[row/3][col/3][num]) {
                    //Converts numbers to characters and fills them into the current cell
                    board[row][col] = String.valueOf(num).charAt(0);
                    rows[row][num] = true;
                    cols[col][num] = true;
                    blocks[row/3][col/3][num] = true;
                    int nextRow = row;
                    int nextCol = col + 1;
                    if (col == 8) {
                        nextRow = row + 1;
                        nextCol = 0;
                    }
                    backtrack(nextRow, nextCol, board);
                    if (solved) {
                        return;
                    }
                    //Recover the decision stage
                    board[row][col] = '.';
                    rows[row][num] = false;
                    cols[col][num] = false;
                    blocks[row/3][col/3][num] = false;
                }
            }
        }
    }
}