Raw2Repo
By Rick

📖快捷切换代码托管平台raw页面到repo页面
🔗github链接 https://github.com/rickhqh/Raw2Repo
✨Features
功能:
- ✅单击 Raw2Repo 插件按钮,即可跳转到相应的代码仓库页面。
- ✅支持 GitHub、Gitee、GitCode 和 GitLab。
- ✅GitHub、Gitee 可以展示相关仓库信息
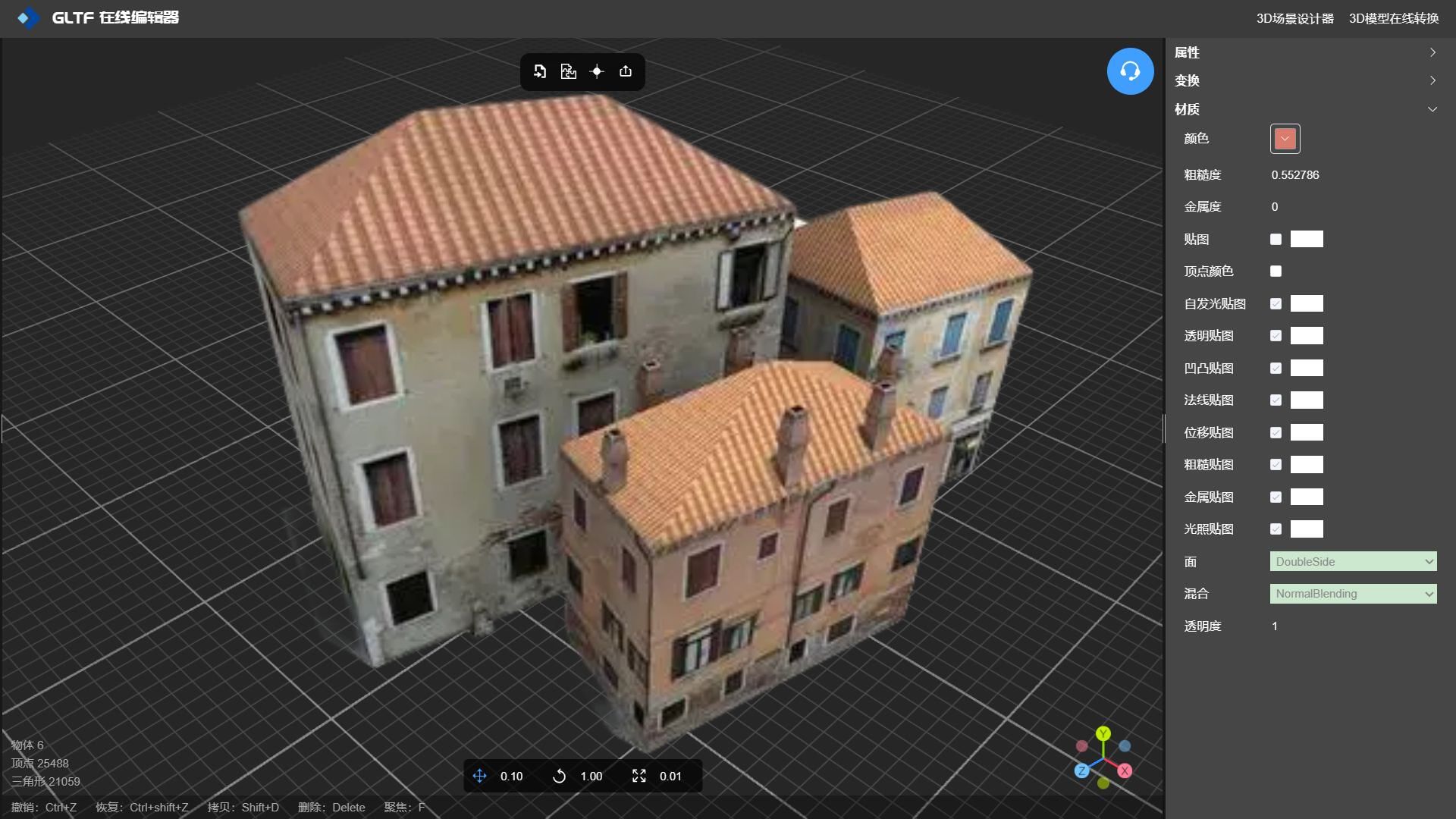
效果:
 |  |
|---|---|
 |  |
TODO
- 提供更多仓库信息
- 提供更多跳转选项
🧩插件用法:
- 下载Releases插件压缩包zip,然后解压
- 打开chorme**扩展程序 ** chrome://extensions/页面,点击加载已解压的扩展程序。 详细教程
- 浏览到任何支持的代码文件的 raw 页面。
- 单击 GO,即可立即切换到相应代码仓库的文件。









![[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-5Laplace Transform of Convolution卷积的拉普拉斯变换](https://img-blog.csdnimg.cn/direct/b4b7f97d69d345758e3e7218bc4a7f5f.png)