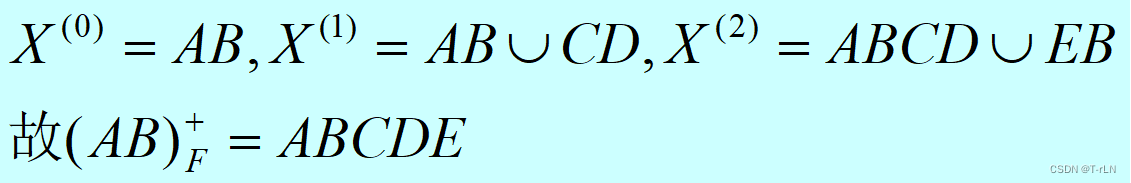在背包问题中,贪心算法通常用来解决0-1背包问题,也就是每种物品都有固定数量,你可以选择拿或者不拿,但不可以拿走部分。以下是一个用C语言实现的贪心算法的例子:
- #include <stdio.h>
- #define MAX_N 1000
- #define MAX_W 100000
- int n, W;
- int w[MAX_N], v[MAX_N], s[MAX_N];
- int f[MAX_N][MAX_W];
- int max(int a, int b) {
- return a > b ? a : b;
- }
- int min(int a, int b) {
- return a < b ? a : b;
- }
- int main() {
- scanf("%d %d", &n, &W);
- for (int i = 0; i < n; i++) {
- scanf("%d %d %d", &w[i], &v[i], &s[i]);
- }
- for (int i = 0; i < n; i++) {
- for (int j = W; j >= w[i]; j--) {
- f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]);
- }
- }
- printf("%d\n", f[n - 1][W]);
- return 0;
- }
在这个例子中,输入包括物品的数量n和背包的总容量W,然后是每个物品的重量w[i],价值v[i]和数量s[i]。在这个版本的背包问题中,每个物品可以取多次。f[i][j]表示在容量为j的背包中,前i个物品能够获得的最大价值。程序最后输出的是在给定背包容量下,所有物品的最大价值。
背包问题的贪心算法主要是针对0-1背包问题,即每种物品都有固定数量,可以选择拿或者不拿,但不可以拿走部分。贪心算法的策略是在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的。
在背包问题中,我们通常用动态规划来求解。在上述代码中,我们用f[i][j]表示前i个物品在容量为j的背包中能够获得的最大价值。初始状态是f[0][j] = 0,表示不取任何物品时的价值为0。然后我们依次考虑每个物品,对于每个物品,我们都尝试放入背包中,并更新f[i][j]。
对于每个物品i,我们从背包容量W开始考虑,逐步减小背包容量,直到背包容量小于物品i的重量。在这个过程中,我们希望找到一个最小的背包容量,使得放入物品i后能够获得最大的价值。这个最小的背包容量就是f[i - 1][j - w[i]],表示前i - 1个物品在容量为j - w[i]的背包中能够获得的最大价值。如果我们将物品i放入容量为j - w[i]的背包中,那么这个背包的容量就增加了w[i],所以能够获得的最大价值就是f[i - 1][j - w[i]] + v[i]。
因此,我们可以得到状态转移方程:f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i])。这个状态转移方程表示,对于前i个物品在容量为j的背包中能够获得的最大价值f[i][j],要么是前i个物品在容量为j的背包中能够获得的最大价值f[i][j],要么是前i - 1个物品在容量为j - w[i]的背包中能够获得的最大价值f[i - 1][j - w[i]] + v[i]。
最后,输出f[n - 1][W],表示前n个物品在容量为W的背包中能够获得的最大价值。
除了上述的贪心算法外,还有一种称为“完全背包”的贪心算法,适用于物品数量不固定的情况。
在完全背包问题中,每种物品的数量是无限的,可以选择拿或者不拿,但不可以拿走部分。以下是一个用C语言实现的完全背包问题的贪心算法:
- #include <stdio.h>
- #define MAX_N 1000
- #define MAX_W 100000
- int n, W;
- int w[MAX_N], v[MAX_N];
- int f[MAX_N][MAX_W];
- int max(int a, int b) {
- return a > b ? a : b;
- }
- int min(int a, int b) {
- return a < b ? a : b;
- }
- int main() {
- scanf("%d %d", &n, &W);
- for (int i = 0; i < n; i++) {
- scanf("%d %d", &w[i], &v[i]);
- }
- for (int i = 0; i < n; i++) {
- for (int j = w[i]; j <= W; j++) {
- f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]);
- }
- }
- printf("%d\n", f[n - 1][W]);
- return 0;
- }
在这个例子中,输入包括物品的数量n和背包的总容量W,然后是每个物品的重量w[i]和价值v[i]。在这个版本的背包问题中,每种物品的数量是无限的,可以选择拿或者不拿,但不可以拿走部分。我们用f[i][j]表示前i个物品在容量为j的背包中能够获得的最大价值。程序最后输出的是在给定背包容量下,所有物品的最大价值。
在完全背包问题中,由于每种物品的数量是无限的,所以可以将每个物品看作是一个整体,而不必考虑其数量。因此,我们可以将每个物品的重量和价值看作是其整体的“单位重量”和“单位价值”。
在贪心算法中,我们采取的策略是在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的。因此,我们可以将每个物品的单位价值除以单位重量得到一个“性价比”,然后按照性价比从高到低的顺序依次考虑每个物品。
具体实现时,我们可以先计算每个物品的单位重量和单位价值,然后按照单位价值的降序排列每个物品。对于每个物品,我们可以依次将其加入背包中,并更新背包的容量和价值。这个过程中需要用到一个二维数组f[i][j],表示前i个物品在容量为j的背包中能够获得的最大价值。
状态转移方程与上面的背包问题类似,可以用以下公式表示:
f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i])其中w[i]表示第i个物品的重量,v[i]表示第i个物品的价值。
最后输出f[n - 1][W],表示前n个物品在容量为W的背包中能够获得的最大价值。