(原创声明:该文是作者的原创,面向对象是FPGA入门者,后续会有进阶的高级教程。宗旨是让每个想做FPGA的人轻松入门,作者不光让大家知其然,还要让大家知其所以然!每个工程作者都搭建了全自动化的仿真环境,只需要双击top_tb.bat文件就可以完成整个的仿真(前提是安装了modelsim),降低了初学者的门槛。如需整个工程请留言(WX:Blue23Light),不收任何费用,但是仅供参考,不建议大家获得资料后从事一些商业活动!)
在数字信号处理中,CIC滤波器是FIR滤波器中最优的一种,其使用了积分,梳状滤波器级联的方式。CIC滤波器由一对或多对积分-梳状滤波器组成,在抽取CIC中,输入信号依次经过积分,降采样,以及与积分环节数目相同的梳状滤波器。
以上是百度上对CIC滤波器的说明,后面还有各种的公式的推导,有兴趣的读者可以好好学习一下,这不是本文的重点,本文主要讲解如何用FPGA设计CIC滤波器。
从定义中我们可以得出,CIC滤波器是FIR滤波器的一种,可以只使用积分和梳状滤波器来实现,也就是说根本没有了FIR的乘法操作,实现非常的简单。
积分器是单极点的IIR滤波器,其状态方程为:
其系统响应为:
梳状滤波器为对称的FIR滤波器,其状态方程为:
其系统响应为:
CIC滤波器是通过将积分器与梳状滤波器进行级联,可以得到CIC滤波器的系统函数响应:
其中N为抽取倍数由于单级CIC的第一旁瓣阻带衰减是固定的13.46dB,无法很好的抑制旁瓣,因此可以通过级联的方式来提升抑制效果。
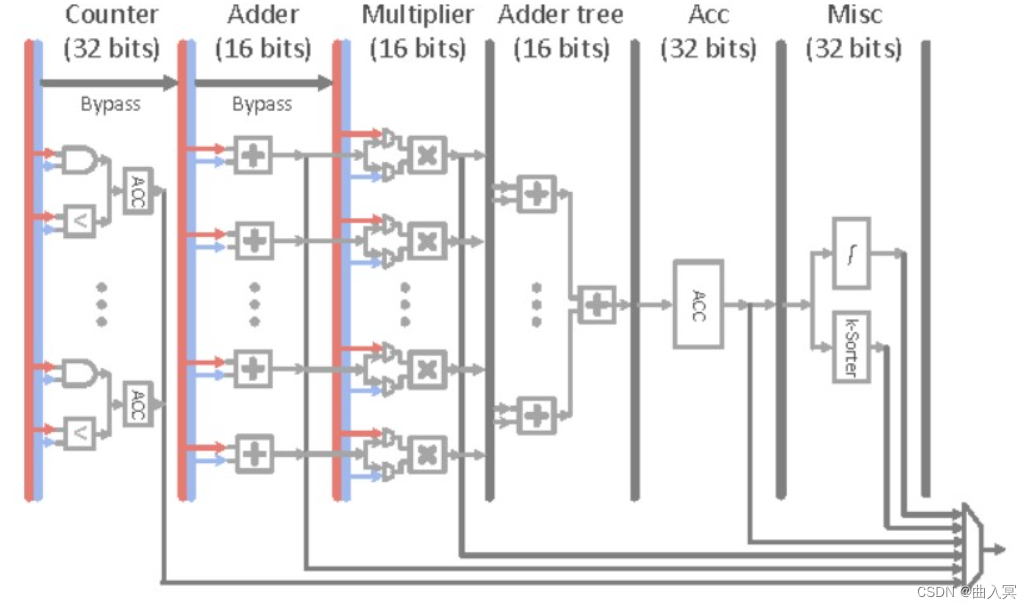
看公式能可能会一头雾水,我们用3级CIC抽取滤波器的示意图来说明,如下所示。CIC抽取滤波器一般用在高速采集信号的降采样上,假如AD的采集速度是Fs,但是系统的处理速度只有Fs/N,和直接抽取或者N个值加权平均相比,CIC抽取是计算复杂度低,系统性能,可以有效的过滤掉噪声和干扰信号。
数据以Fs(假设100MHz)的频率输入滤波器,那数据先通过3级的积分滤波器一直进行累加。假如我们希望得到Fs的16分频的采样数据,那就将积分滤波器的最后一级输出以Fs/N(6.25MHz)的频率进入梳状滤波器,梳状滤波器其实是微分运算,即当前值减去上一次的值。经过3次的梳状滤波器,最后1级的结果即为抽取的数值。

CIC滤波器的设计还有一个问题,就是数据位数的扩展。假设输入数据是8位,因为积分滤波器一直在累计,中间的寄存器一定要进行数据位的扩展。这儿有一个扩展的公式,就是数据的最大位宽是8+K*log2(N*M),K是积分滤波器和梳状滤波器的级数,这儿K=3,N是降采样的倍数,这儿N=16,M是每次采样的样本个数,这儿M=1;所以扩展后数据的最大位宽是8+3*log2(16)=20,方便起见,中间的寄存器可以都取20位即可。
如下所示,CIC降采样滤波器相关信号的定义,参数W=20是中间寄存器的位宽,DIV_NUM=16是降采样的倍数,SIGNAL_NUM是符号位扩展的位数。
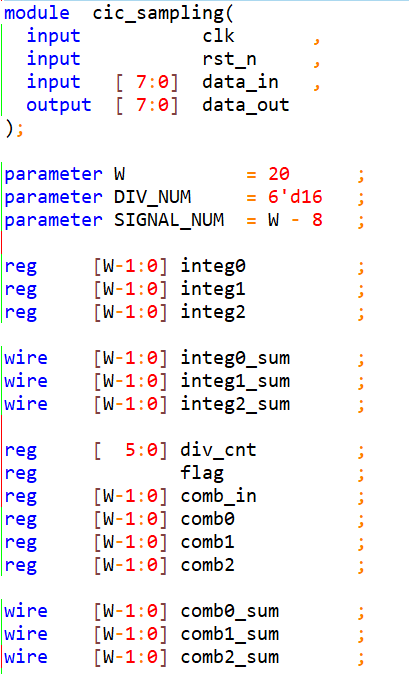
用时序打拍的方式完成积分累计值的3级传递,用组合逻辑实现积分器的累加。用计数器div_cnt产生flag控制系统降采样。

用时序打拍的方式完成梳状滤波器微分值的3级传递,用组合逻辑实现梳状滤波器的微分运算。最后一级微分值的高8位就是CIC按照16倍降采样抽取的最终数值。

本工程新建了一个cic_top文件,用来例化cic_sampling和前面课程中的正弦波生成器gen_sin,将正弦波以数据以100MHz的频率读出,经过cic_sampling后,以6.25MHz的频率输出。

新建仿真文件后,双击sim目录下的top_tb.bat文件,完成系统的自动化仿真。

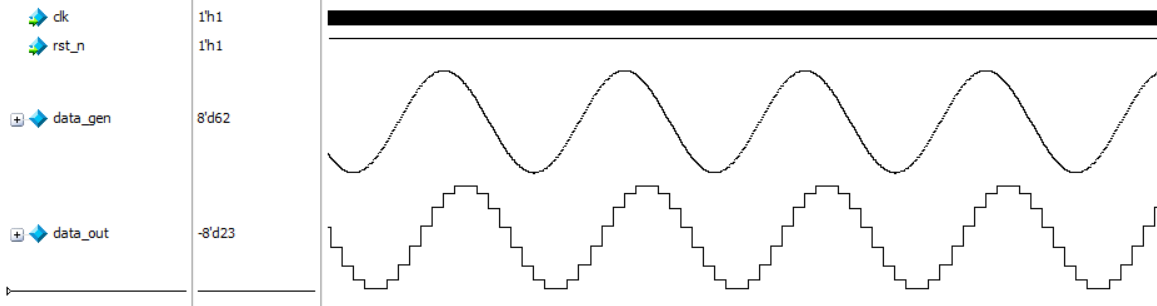
modelsim的仿真波形如下所示,CIC降采样抽取后的波形相位有一些滞后,输出的波形也没有失真,功能开发是正确的。
其实CIC不光可以降采样抽取,还是可以升采样进行插值,这个我们下节课进行讲解。