【力扣热题100】287. 寻找重复数
- 写在最前面
- 理解解决 "寻找重复数" 问题的算法
- 问题描述
- 弗洛伊德的乌龟和兔子方法
- 为什么这个方法有效?
- 代码
- 复杂度
- 总结回顾
写在最前面
刷一道力扣热题100吧
难度中等
https://leetcode.cn/problems/find-the-duplicate-number/?envType=study-plan-v2&envId=top-100-liked
一年半前做过这题,但是时间复杂度不够。现在重新学一下
主要是用到了弗洛伊德的乌龟和兔子方法
算法预览:
-
初始化:从两个指针开始,“乌龟"和"兔子”,都指向第一个元素。
-
第一阶段 - 检测循环:每次移动乌龟一步(
tortoise = nums[tortoise]),兔子两步(hare = nums[nums[hare]])。继续这个过程,直到他们在循环中相遇。 -
第二阶段 - 找到循环的入口:将乌龟重置到数组的开头。将乌龟和兔子都每次移动一步。他们再次相遇的地方就是循环的入口,对应着重复的数字。
理解解决 “寻找重复数” 问题的算法
在处理 “287. 寻找重复数” 这个问题时,我们面临一个独特的挑战:在不修改数组并且只使用常数额外空间的情况下找出数组中的一个重复数字。
这种情况使得传统的方法,如排序或哈希表变得不可行。
然而,有一种巧妙的方法可以解决这个问题,这就是著名的弗洛伊德的乌龟和兔子算法,一种用于检测循环的方法。
问题描述
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
提示:
- 1 <= n <= 105
- nums.length == n + 1
- 1 <= nums[i] <= n
- nums 中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
- 如何证明 nums 中至少存在一个重复的数字?
- 你可以设计一个线性级时间复杂度 O(n) 的解决方案吗?
弗洛伊德的乌龟和兔子方法
这个算法主要用于检测值序列中的循环。以下是我们适应我们问题的方式:
-
初始化:从两个指针开始,“乌龟"和"兔子”,都指向第一个元素。
-
第一阶段 - 检测循环:每次移动乌龟一步(
tortoise = nums[tortoise]),兔子两步(hare = nums[nums[hare]])。继续这个过程,直到他们在循环中相遇。 -
第二阶段 - 找到循环的入口:将乌龟重置到数组的开头。将乌龟和兔子都每次移动一步。他们再次相遇的地方就是循环的入口,对应着重复的数字。
为什么这个方法有效?
关键的洞见是将数组视为一个链表,其中每个元素指向下一个元素的位置。例如,在一个数组 [2, 5, 1, 1] 中,2 指向位置 2,5 指向位置 1,形成了一个循环。由于存在重复,因此一定存在一个循环。该算法有效地找到了这个循环及其入口。
代码
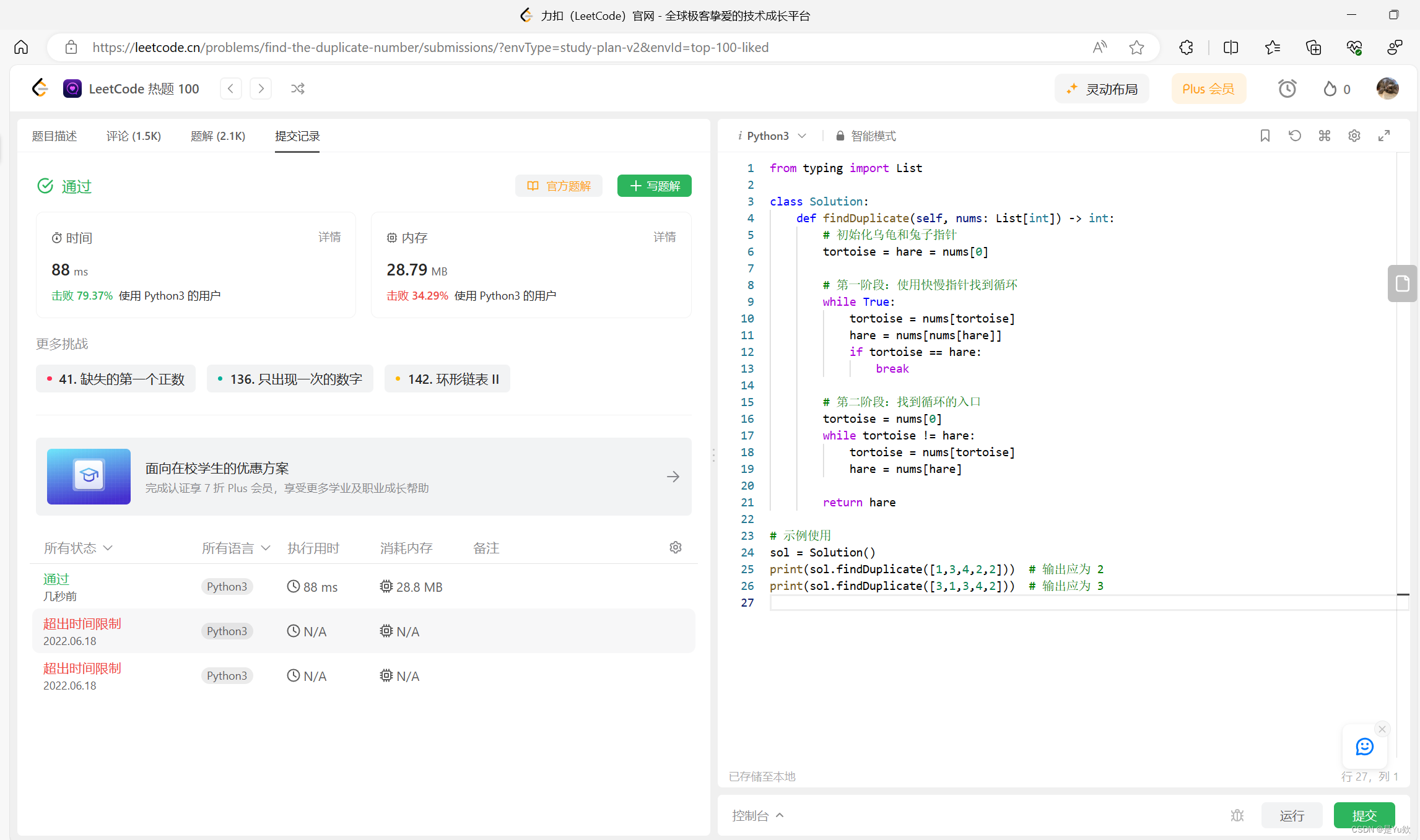
from typing import List
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
# 初始化乌龟和兔子指针
tortoise = hare = nums[0]
# 第一阶段:使用快慢指针找到循环
while True:
tortoise = nums[tortoise]
hare = nums[nums[hare]]
if tortoise == hare:
break
# 第二阶段:找到循环的入口
tortoise = nums[0]
while tortoise != hare:
tortoise = nums[tortoise]
hare = nums[hare]
return hare
# 示例使用
sol = Solution()
print(sol.findDuplicate([1,3,4,2,2])) # 输出应为 2
print(sol.findDuplicate([3,1,3,4,2])) # 输出应为 3
复杂度
这种方法的美妙之处在于其效率:
- 时间复杂度:O(n)。算法的两个阶段都在线性时间内运行。
- 空间复杂度:O(1)。只使用了两个额外变量(乌龟和兔子)。
总结回顾
弗洛伊德的乌龟和兔子算法是解决涉及序列中循环的问题的一个巧妙的解决方案。它在寻找数组中的重复数字的应用是一个典型的例子,展示了如何跳出常规思维框架,将算法适应于独特问题。这个解决方案不仅满足了常数空间和不修改数组的约束,而且做到了高效。