1.优先级队列
由前文队列queue可知,队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,在此情况下,使用队列queue显然不合适,
同时在我们生活场景中也有类似于这中优先事情处理的情况,在医院看病的时候大家都在排队,突然有一个头上插了一把刀的老爷爷也来排队,这时候虽然大家都很急着去看病,但是出于老爷爷情况紧急,所以大家都会默认让老爷爷优先去见医生,而不是让老爷爷按照一般的规则去老老实实的排队;
考虑到随时会遇到上述这种情况,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数据结构就是优先级队列(Priority Queue)。
2.初识堆
JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。
2.1 堆的概念
如果有一个关键码的集合K = {k0,k1, k2,…,kn-1},把它的所有元素按完全二叉树的顺序存储方式存储 在一 个一维数组中,并满足:Ki = K2i+1 且 Ki >= K2i+2) i = 0,1,2…,则称为 小堆(或大 堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质
堆中某个节点的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树。
2.1.1 小根堆

如上图小根堆的逻辑结构所示,在一颗大的完全二叉树中的小二叉树中,该小二叉树的根节点远远小于该树左右子节点,且这时候不考虑左右子节点的数值哪个大;
2.1.2 大根堆

如上图大根堆的逻辑结构所示,给一颗大的完全二叉树中的小二叉树中,该小二叉树的根节点远远大于于该树左右子节点,且这时候不考虑左右子节点的数值哪个大;
2.2 堆的存储方式
从堆的概念可知,堆是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储,如下图所示堆的存储图解;(堆是将一个一维数组中的数据按照层序遍历的规则将这些数据存储到一个完全二叉树里的完全二叉树)
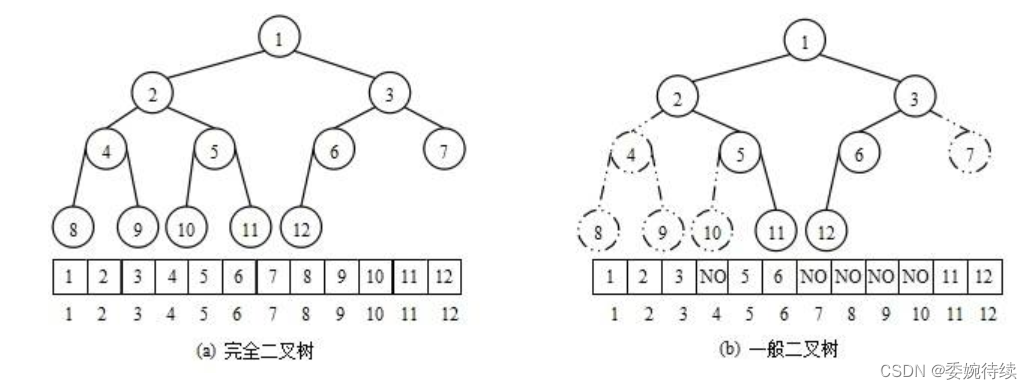
注意:由该图中的逻辑结构和存储结构可知,对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了通过一维存储结构能够还原二叉树,一维存储空间中必须要存储空节点,就会导致该存储空间利用率比较低。
将元素存储到数组中后,可以根据本主初识二叉树章节的性质5对树进行还原。
假设i为节点在数组中的下标,则有:
如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
2.3 堆的创建(小根堆)
2.3.1 堆向下调整
思考:
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据,如何将其创建成堆,首先按照堆的规则将以上数剧放入到完全二叉树里面,如下图所示:
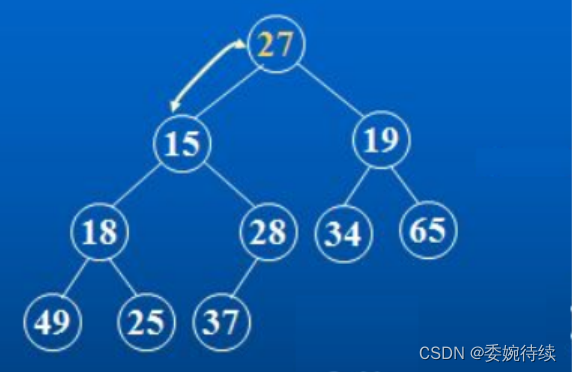
仔细观察上图后发现:当前根节点27的左右子树已经完全满足堆的性质,因此只需将根节点向下调整好即可。
调整过程如下:
1. 让parent标记需要调整的节点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
2. 如果parent的左孩子存在,即:child < size, 进行以下操作,直到parent的左孩子不存在 2.1parent右孩子是否存在,存在找到左右孩子中最小的孩子,让child进行标
2.2将parent与较小的孩子child比较,如果:
2.2.1 parent小于较小的孩子child,调整结束
2.2.2 否则:交换parent与较小的孩子child,交换完成之后,parent中大的元素向下移动,可能导致子树不满足对的性质,因此需要继续向下调整,即parent = child;child = parent*2+1(左子树); 然后继续2
详细调整图解如下图所示:

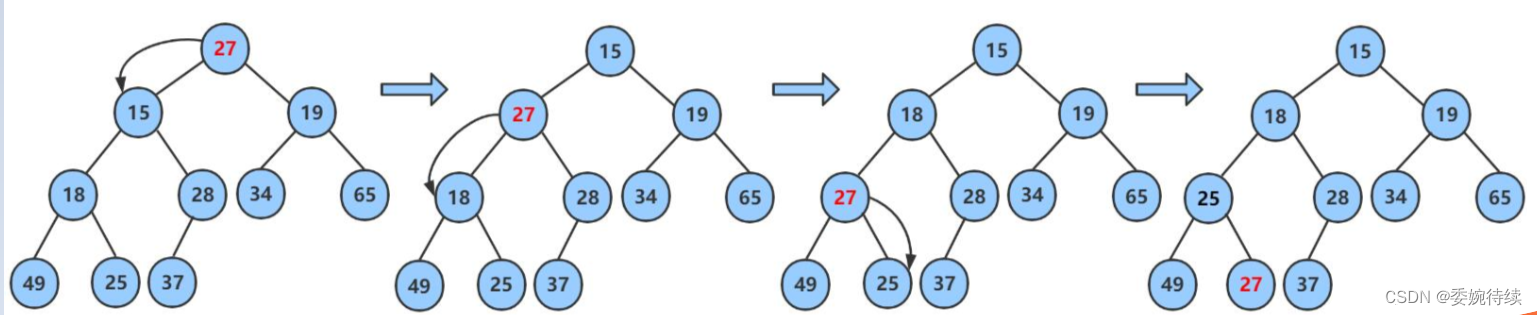
2.3.2 小根堆代码实现
package com.bit.demo1;
public class MySmallHeap {
public void shiftDown(int[] array, int parent) {
//child和parent时数组存储的节点的索引
// child先标记parent的左孩子,因为parent可能右左没有右
int child = 2*parent + 1;
int size = array.length;//所有节点的数目
while(child < size ) {
//主要保证当前访问到的child都在所有节点的范围内,是有效的
//child+1是二叉树的最后一个节点
// 如果右孩子存在,找到左右孩子中较小的孩子,用child进行标记
if(child + 1 < size) {
if(array[child + 1] < array[child]) {
child = child + 1;
}
}
// 如果最小的孩子比其父亲还小,说明该结构没有满足堆的特性,进行交换
if(array[child] < array[parent]) {
int tmp = array[parent];
array[parent] = array[child];
array[child] = tmp;
} else {
//满足就退出循环
break;
}
// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整
parent = child;
child = 2*parent + 1;
}
}
}
2.3.3 小根堆代码测试
public static void main(String[] args) {
MySmallHeap mySmallHeap = new MySmallHeap();
int[] array = {27,15,19,18,28,34,65,49,25,37};
System.out.println("调整前:");
for(int i = 0; i < array.length ; i++) {
System.out.print(array[i] + " ");
}
for(int parent = (array.length-2)/2 ; parent >= 0; parent --) {
mySmallHeap.shiftDown(array, parent);
}
System.out.println();
System.out.println("调整后:");
for(int i = 0; i < array.length ; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}关于最初的parent索引 ?
测试结果如下图所示:
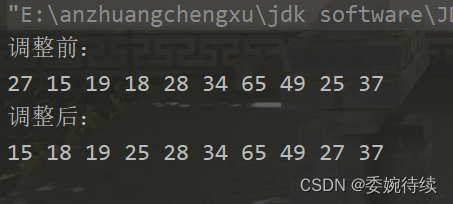
注意:在调整以parent为根的二叉树时,必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
最坏的情况即图示的情况,从根一路比较到叶子,比较的次数为完全二叉树的高度,即时间复杂度为![]()
2.4 建堆的时间复杂度
2.4.1 建堆的步骤图解
对于普通的序列{ 1,5,3,8,7,6 },我们需要建立大堆,即根节点的左右子树不满足堆的特性,又该如何调整呢,其中里面的细节如下:
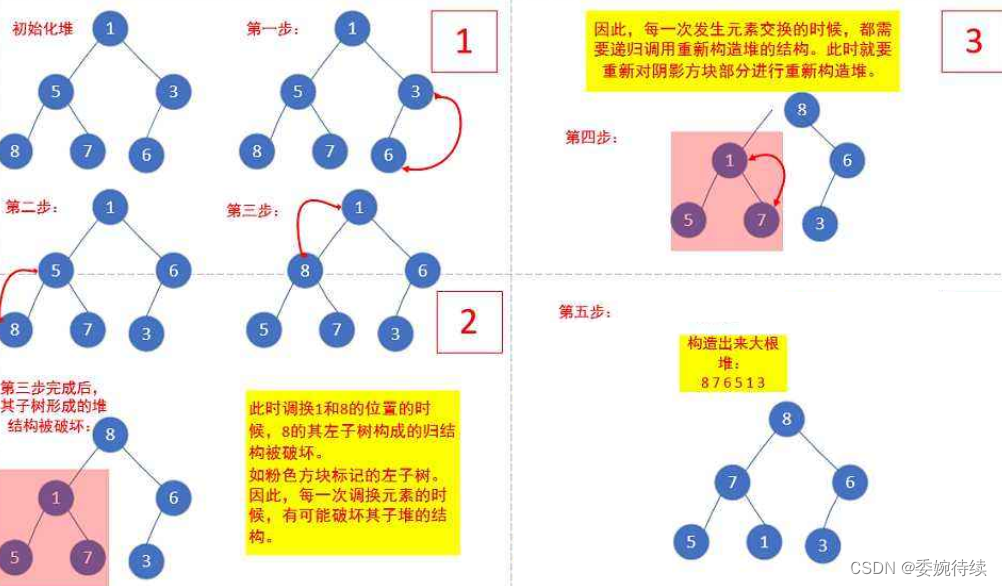
大概思路:
找倒数第一个非叶子节点(最右侧的最小子树根节点),从该节点位置开始往前进行按照根堆的规则运作,一直运作到根节点,这时候才确定根节点的数值;
因为为了根节点导致下面的不同子树的结构都发生了变化,所以接下来确定索引为1的根节点的数字,这样就需要重复上述的步骤;
就这样重复上面两个步骤,知道确定最右侧最小子树的根节点(索引为(arr.length-2)/2)的数值,我们的整体过程才算结束;
2.4.2 时间复杂度求解图解
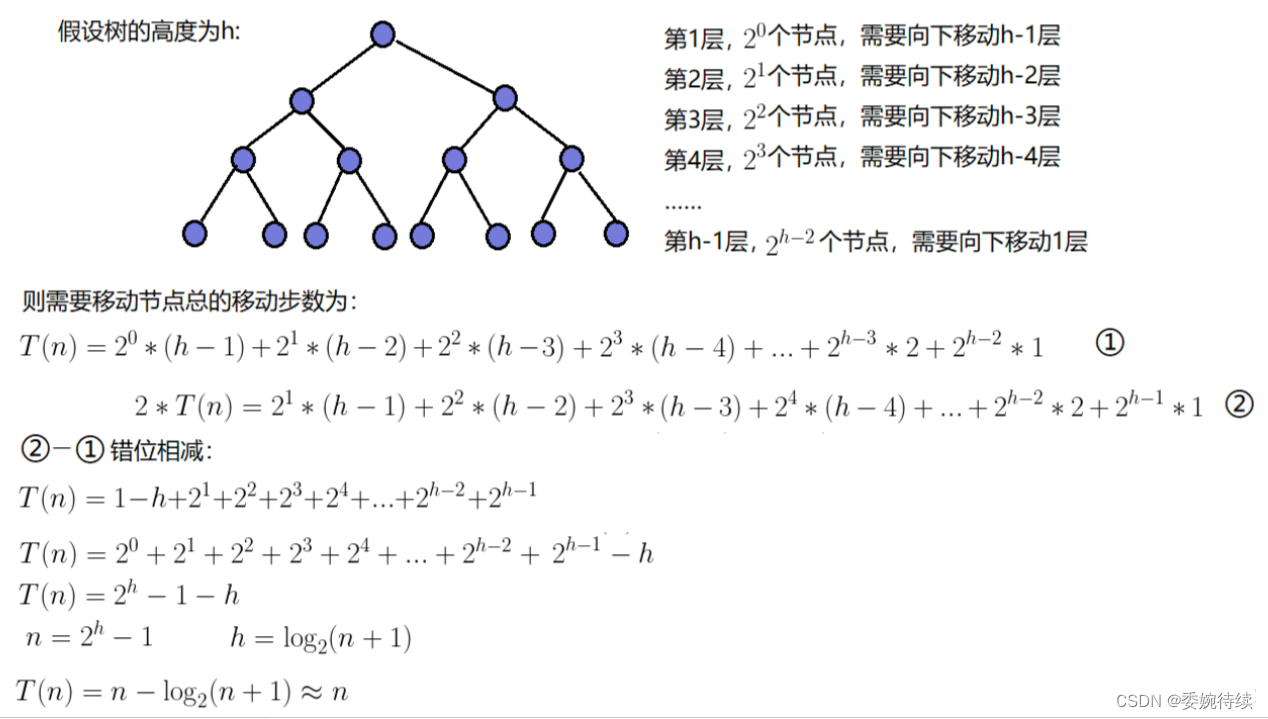
至此可得:建堆的时间复杂度为O(N)
ps:本次的内容就到这里了,如果喜欢的话就请一键三连哦!!!