数据结构与算法（六）分支限界法（Java）

news2024/11/28 15:41:09

目录

    • 一、简介
      • 1.1 定义
      • 1.2 知识回顾
      • 1.3 两种解空间树
      • 1.4 三种分支限界法
      • 1.5 回溯法与分支线定法对比
      • 1.6 使用步骤
    • 二、经典示例：0-1背包问题
      • 2.1 题目
      • 2.2 分析
        • 1）暴力枚举
        • 2）分支限界法
      • 2.3 代码实现
        • 1）实现广度优先策略遍历
        • 2）实现限界函数来剪枝

一、简介

1.1 定义

分支限界法 是使用 广度优先策略，依次生成 扩展节点 上的所有分支。就是 把问题的可行解展开，再由各个分支寻找最佳解。

分支限界法 与 回溯法 类似，都是 递归 + 剪枝，区别在于回溯法使用的是深度优先策略，而分支限界法使用的是广度优先策略。

1.2 知识回顾

  • 扩展结点： 一个 正在生成儿子 的结点，称为扩展结点。
  • 活结点： 一个 自身已生成但其儿子还没有全部生成 的结点，称为活结点。
  • 死结点： 一个 所有儿子已经全部生成 的结点，称为死结点。

深度优先策略：

  • 如果对一个扩展结点 R，一旦生成了它的一个儿子 C，就把 C 当作新的扩展结点。
  • 在完成对子树 C（以 C 为根的子树）的穷尽搜索之后，将 R 重新变成扩展结点，继续生成 R 的下一个儿子（如果存在）。

广度优先策略：

  • 在一个扩展结点变成死结点之前，它一直是扩展结点。

剪枝函数：

剪枝函数：当某个顶点没有希望，则其所在的树枝可以减去。

剪枝函数一般有两种：

  • 约束函数： 剪去不满足约束条件的路径。
  • 限界函数： 减去不能得到最优解的路径。

1.3 两种解空间树

子集树（Subset Trees）：

  • 当所给问题是 从 n 个元素的集合中找出满足某种性质的子集 时，相应的解空间树称为 子集树。

若 Sn 表示 n 结点子树的数量，在子集树中，|S0| = |S1| = ... = |Sn-1| = c，即每个结点有相同数目的子树，通常情况下 c = 2，所以子树中共有 2^n 个叶子结点。因此，遍历子集树的时间复杂度为 O(2^n)。

排列树（Permutation Trees）：

  • 当所给问题是 确定 n 个元素满足某种性质的排列 时，相应的解空间树称为排列树。

若 Sn 表示 n 结点子树的数量，在排列树中，通常情况下 |S0| = n, |S1| = n-1, ..., |Sn-1| = 1。所以，排列树中共有 n! 个叶子结点。因此，遍历排列树的时间复杂度为 O(n!)。

1.4 三种分支限界法

不同于回溯法，在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点，通过 剪枝函数 将导致不可行解或非最优解的儿子结点舍弃，其余 儿子结点被加入活结点表中。

然后，从 活结点表 中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个 过程一直持续到 找到所需解 或 活结点表为空 为止。

根据活结点表的形成方式不同分为 三种分支限界法：

  • FIFO分支限界法：活结点表是 队列，按照队列先进先出（FIFO）原则选取下一个结点为扩展结点。
  • LIFO分支限界法：活结点表是 堆栈，按照堆栈先今后出（LIFO）原则选取下一个结点为扩展结点。
  • LC分支限界法：活结点是 优先权队列（Low Cost），按照优先队列中规定的优先权选取具有最高优先级的活结点成为新的扩展结点。
    • 结点优先权： 在其分支下搜索一个答案状态需要花费的代价越小，优先级越高。

1.5 回溯法与分支线定法对比

算法名称对解空间树的搜索方式存储结点的常用数据结构结点存储特性求解目标空间复杂度
回溯法深度优先搜索（DFS）递归；
非递归时使用堆栈		活结点的所有可行子结点被遍历后才被从栈中弹出（结点可能多次成为扩展结点）。找出解空间树中满足约束条件的所有解。子集树：O(n)
排列树：O(n)
分支限界法广度优先搜索（BFS）
最小消耗优先搜索（LC）		队列；堆栈、优先队列每个活结点只有一次成为扩展结点的机会。找出满足约束条件的一个解，或在满足约束条件的解中找出某种意义下的最优解。子集树：O(2^n)
排列树：O(n!)

1.6 使用步骤

  1. 首先 确定一个合理的限界函数，并 根据限界函数确定目标函数的界；
  2. 然后 按照广度优先策略搜索问题的解空间树；
  3. 在扩展结点处，生成所有儿子结点，估算所有儿子结点对目标函数的可能取值，舍弃不可能通向最优解的结点（剪枝），将其余结点加入到活结点表（队列/栈）中；
  4. 在当前活结点表中，依据相应的分支线定法（FIFO、LIFO、LC），从当前活结点表中选择一个结点作为扩展结点；
  5. 重复 4~3 步，直到 找到所需的解 或 活结点表为空。

二、经典示例：0-1背包问题

2.1 题目

假定有N=4件商品，分别用A、B、C、D表示。每件商品的重量分别为 3kg、2kg、5kg和4kg，对应的价值分别为 66元、40元、95元和40元。现有一个背包，可以容纳的总重量位 9kg，问：如何挑选商品，使得背包里商品的 总价值最大？

2.2 分析

0-1背包问题，实际上就是排列组合的问题。

1）暴力枚举

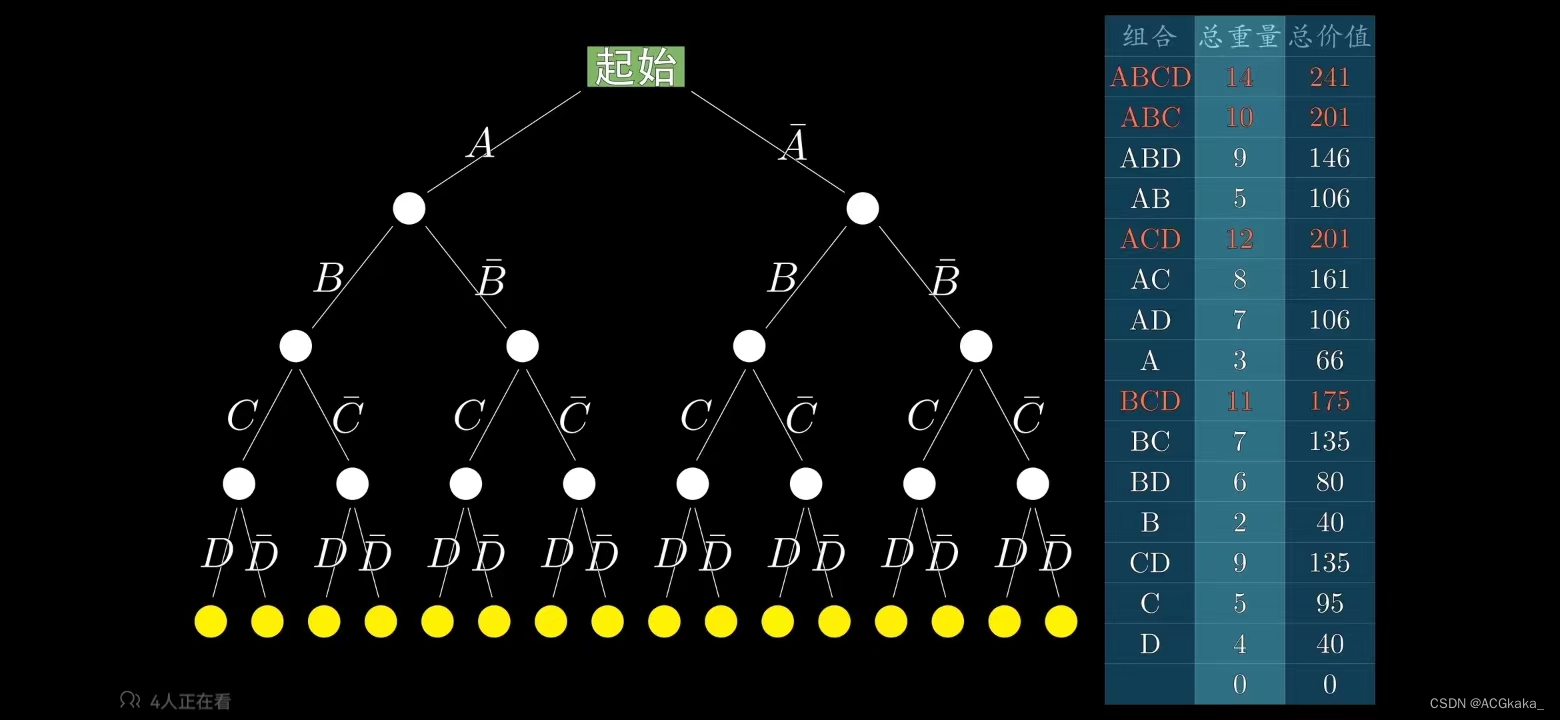
假如我们用A表示物品A存在；A（上划线）表示物品A不存在。暴力枚举所有可能的情况如下：

最优解： A 物品+ C 物品 = 161 价值

在这里插入图片描述

2）分支限界法

首先根据 价值/重量 进行从大到小进行排序，排序结果如下：

  1. 重量：3，价值：66，每份重量价值：22；
  2. 重量：2，价值：40，每份重量价值：20；
  3. 重量：5，价值：95，每份重量价值：19；
  4. 重量：4，价值：40，每份重量价值：10；

假如我们用A表示物品A存在；A（下划线）表示物品A不存在。解空间树 如下：

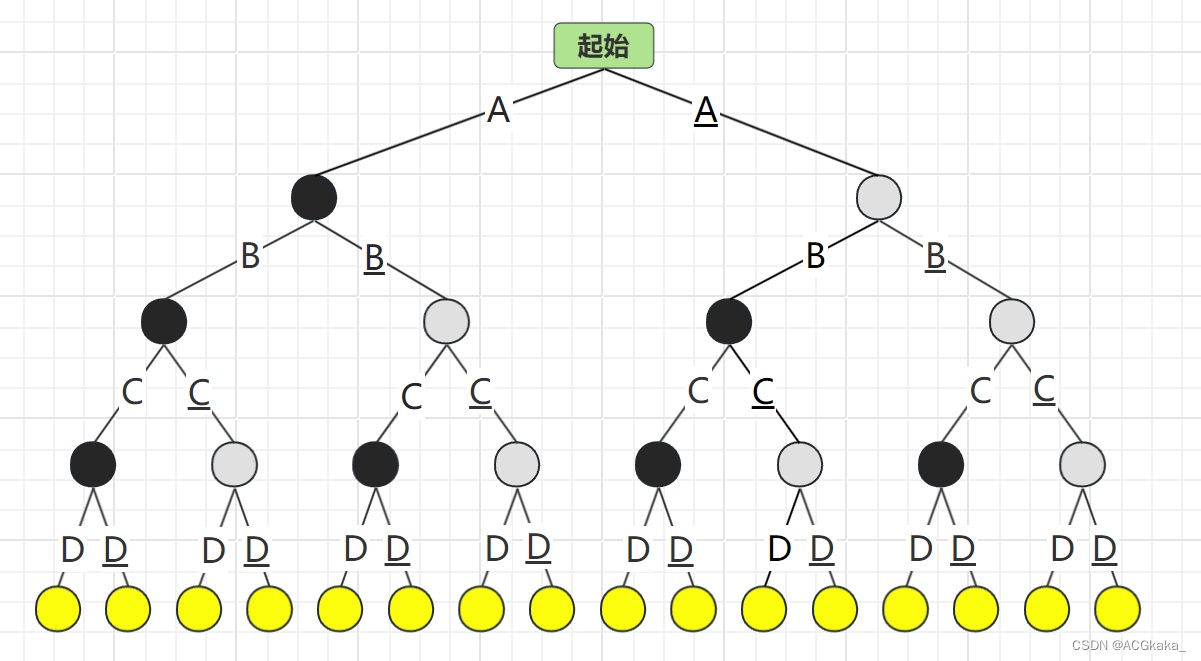
在这里插入图片描述

首先根据 A 物品的存在情况进行计算，A存在时最优价值为182，A不存在时最优价值为155。选择 最优价值更高的情况：A结点。

物品列表：A

背包价值：66

最优队列： A（182）> A（155）

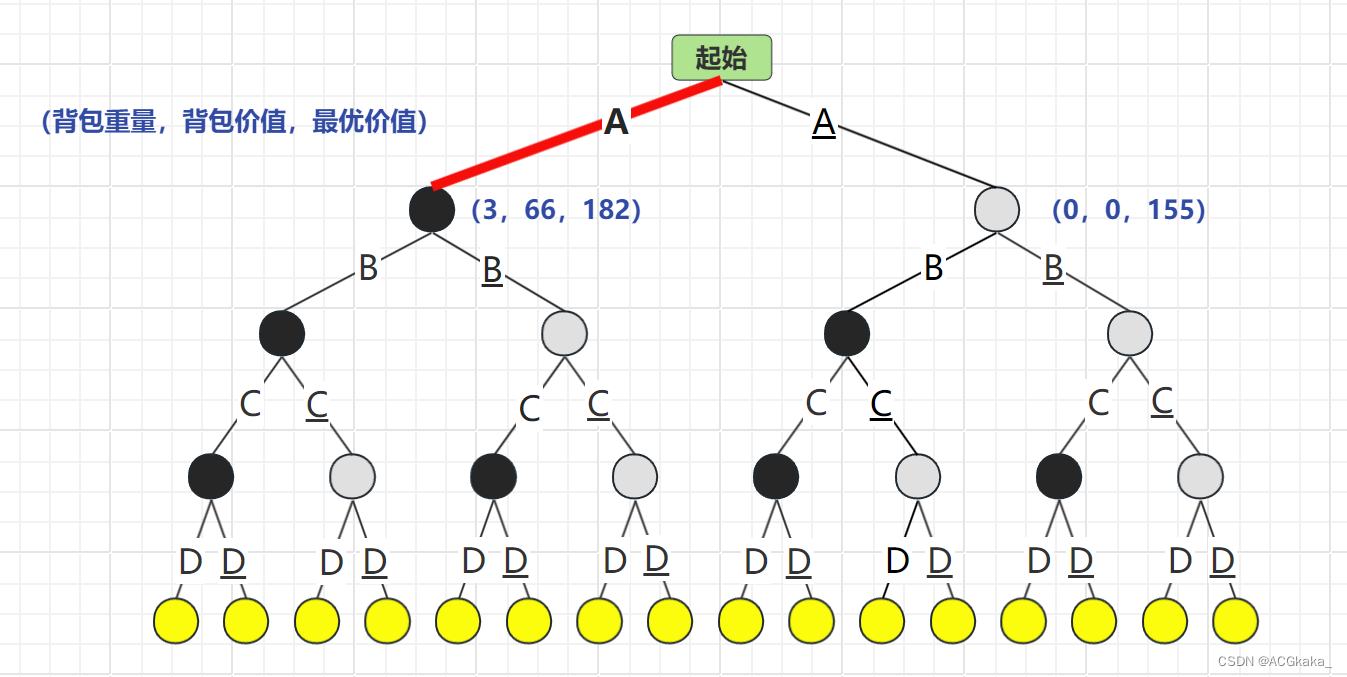
在这里插入图片描述

弹出 A 结点，再根据 B 物品的存在情况进行计算，B存在时最优价值为182，B不存在时最优价值为171。选择 最优价值更高的情况：B结点。

物品列表：A、B

背包价值：106

最优队列： B（182）> B（171）> A（155）

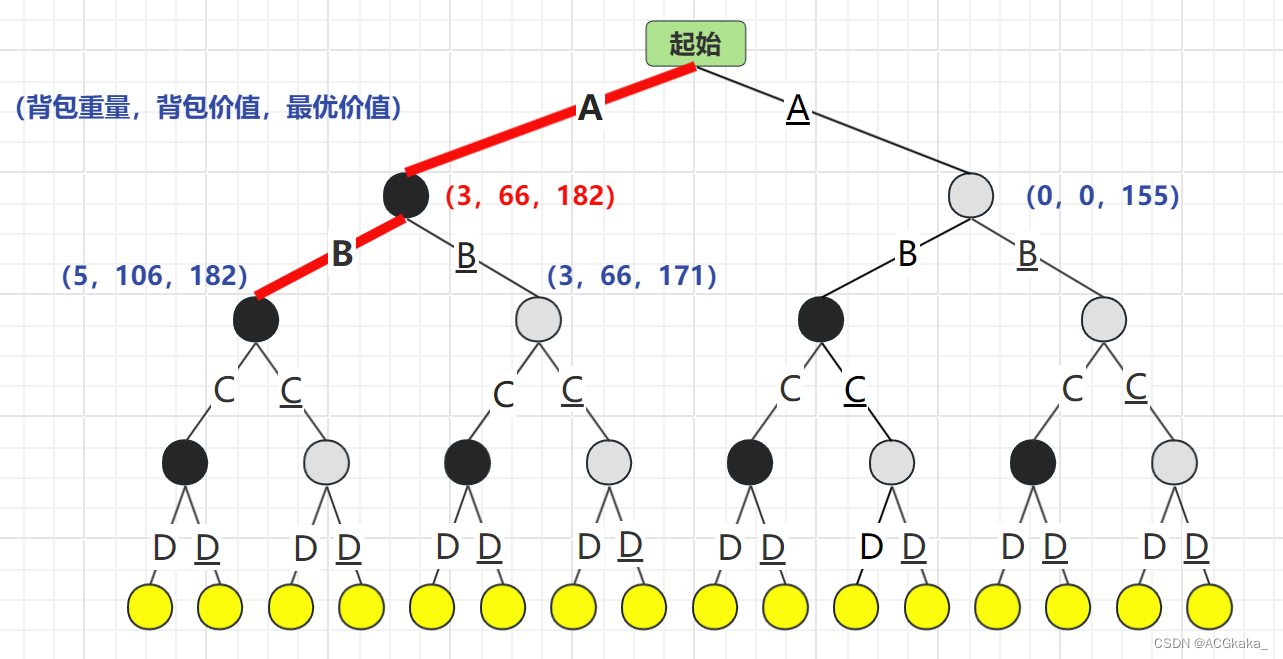
在这里插入图片描述

弹出 B 结点，再根据 C 物品的存在情况进行计算，C存在时超重×，C不存在时最优价值为146。选择 最优价值更高的情况：B结点。

物品列表：A

背包价值：66

最优队列： B（171）> A（155）> C（146）

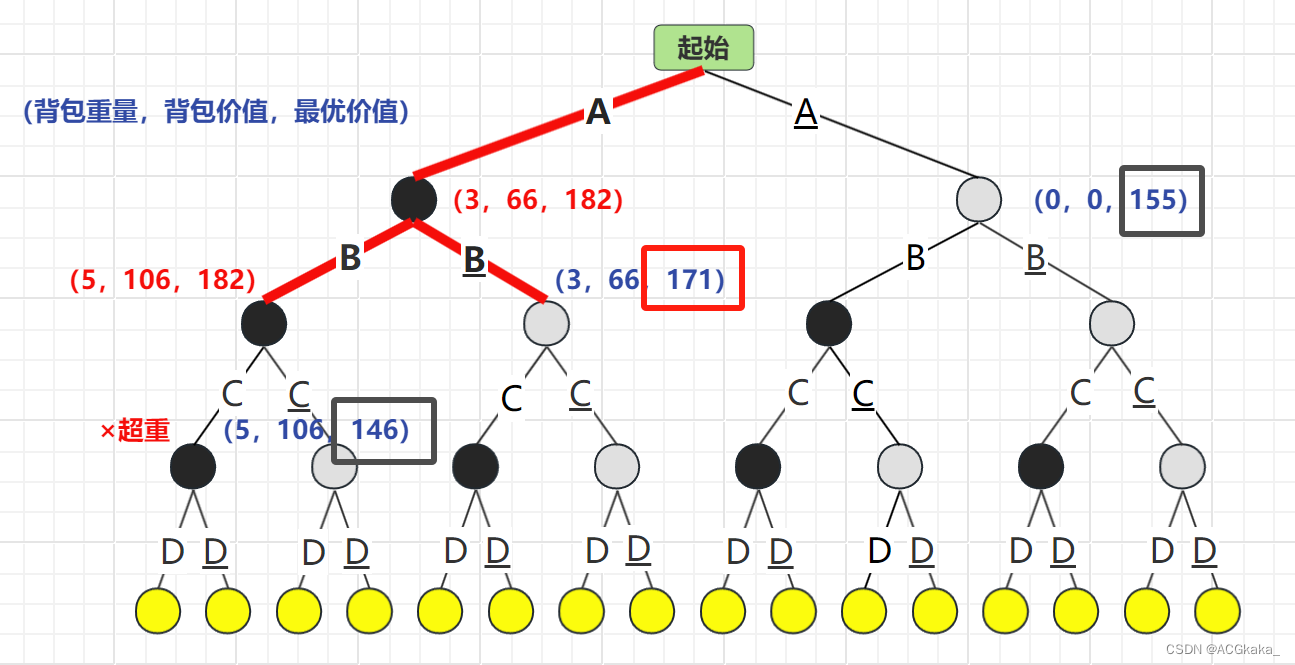
在这里插入图片描述

弹出 B 结点，再根据 C 物品的存在情况进行计算，C存在时最优价值为171，C不存在时最优价值为106，由于 106 不大于已有最大价值 161，舍弃。选择 最优价值更高的情况：C结点。

物品列表：A、C

背包价值：161

最优队列： C（171）> A（155）> C（146）

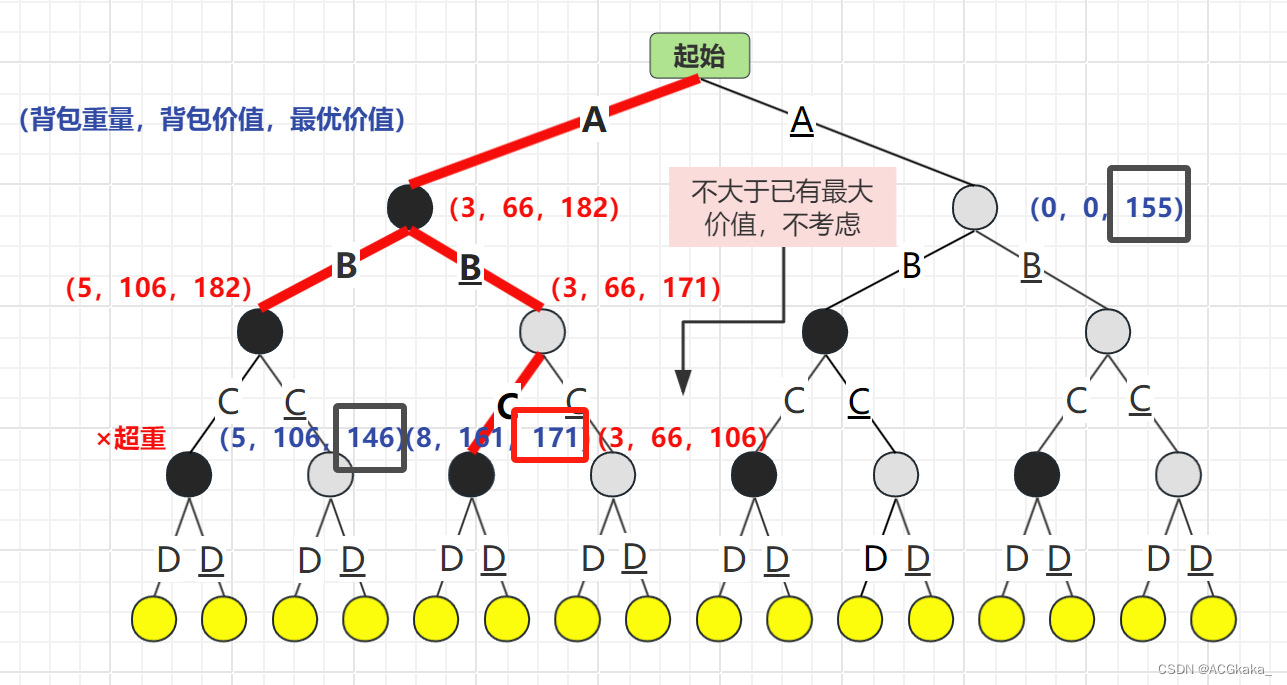
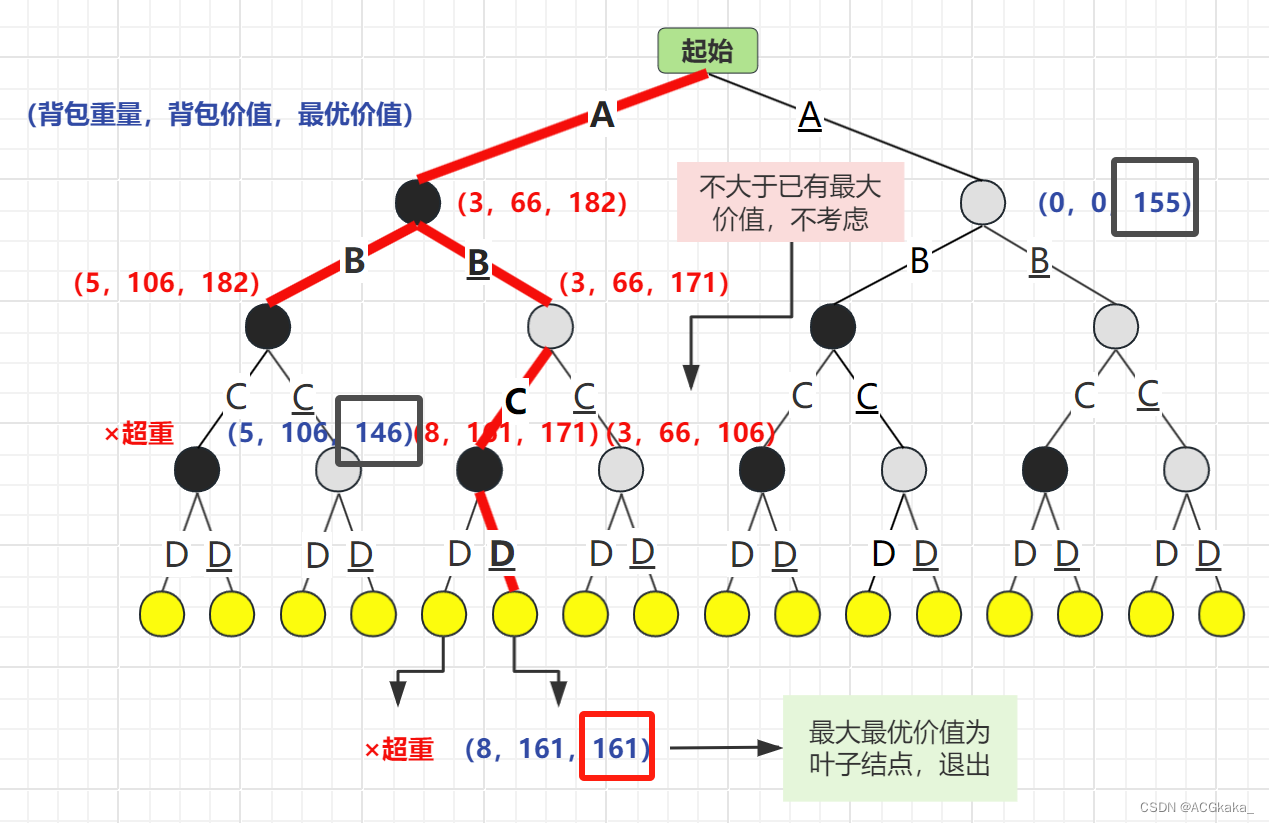
在这里插入图片描述

弹出 C 结点，再根据 D 物品的存在情况进行计算，D存在时超重×，D不存在时最优价值为161。由于此结点已为叶子结点，退出循环。

物品列表：A、C

背包价值：161

在这里插入图片描述

2.3 代码实现

为了方便理解，这里分两步实现：

  • 实现广度优先策略遍历；
  • 实现限界函数来剪枝。
1）实现广度优先策略遍历
public static void main(String[] args) {
    Solution solution = new Solution();
    int[][] arr1 = {{3,66},{2,40},{5,95},{4,40}};
    long start1 = System.currentTimeMillis();
    long start2 = System.nanoTime();
    // 执行程序
    int result = solution.knapsack(arr1, 9);
    long end1 = System.currentTimeMillis();
    long end2 = System.nanoTime();
    System.out.println(result);
    System.out.println("耗时：" + (end1 - start1) + " ms，" + (end2 - start2) + " ns");
}

public int knapsack(int[][] nums, int capacity) {
    Node rootNode = new Node(0, 0, 0);
    Queue<Node> queue = new ArrayDeque<>();
    queue.add(rootNode);
    int maxValue = 0;
    while (!queue.isEmpty()) {
        Node node = queue.poll();
        if (node.index >= nums.length) {
            break;
        }
        // 左节点：放入背包
        if (node.bagWeight + nums[node.index][0] <= capacity) {
            Node newLeftNode = new Node(node.index + 1, node.bagWeight + nums[node.index][0], node.bagValue + nums[node.index][1]);
            queue.add(newLeftNode);
            maxValue = Math.max(maxValue, newLeftNode.bagValue);
        }
        // 右节点：不放入背包
        Node newRightNode = new Node(node.index + 1, node.bagWeight, node.bagValue);
        queue.add(newRightNode);
    }
    return maxValue;
}

static class Node {
    /**
     * 索引（第几个物品）
     */
    private int index;
    /**
     * 背包容量
     */
    private int bagWeight;
    /**
     * 背包价值
     */
    private int bagValue;

    public Node(int index, int bagWeight, int bagValue) {
        this.index = index;
        this.bagWeight = bagWeight;
        this.bagValue = bagValue;
    }
}
2）实现限界函数来剪枝
public static void main(String[] args) {
    Solution solution = new Solution();
    int[][] arr1 = {{3,66},{2,40},{5,95},{4,40}};
    long start1 = System.currentTimeMillis();
    long start2 = System.nanoTime();
    // 执行程序
    int result = solution.knapsack(arr1, 9);
    long end1 = System.currentTimeMillis();
    long end2 = System.nanoTime();
    System.out.println(result);
    System.out.println("耗时：" + (end1 - start1) + " ms，" + (end2 - start2) + " ns");
}

public int knapsack(int[][] nums, int capacity) {
    // 由于使用了贪心算法，需要先进行排序
    Arrays.sort(nums, Comparator.comparingDouble(o -> -1.0 * o[1] / o[0]));
    Node rootNode = new Node(0, 0, 0);
    // 优先队列（贪心算法，按照最优价值排序）
    PriorityQueue<Node> queue = new PriorityQueue<>();
    queue.add(rootNode);
    int maxValue = 0;
    // 遍历，直到最大最优价值为某一叶子结点
    while (queue.size() > 0 && queue.peek().index < nums.length) {
        Node node = queue.poll();
        // 左节点：放入背包
        Node newLeftNode = new Node(node.index + 1, node.bagWeight + nums[node.index][0], node.bagValue + nums[node.index][1]);
        int newLeftUpBound = newLeftNode.getUpBound(nums, capacity);
        if (newLeftUpBound >= maxValue && newLeftNode.bagWeight <= capacity) {
            queue.add(newLeftNode);
            maxValue = Math.max(maxValue, newLeftNode.bagValue);
        }
        // 右节点：不放入背包
        Node newRightNode = new Node(node.index + 1, node.bagWeight, node.bagValue);
        int newRightUpBound = newRightNode.getUpBound(nums, capacity);
        if (newRightUpBound >= maxValue) {
            queue.add(newRightNode);
        }
    }
    return maxValue;
}

static class Node implements Comparable<Node> {
    /**
     * 索引（例：第 1个物品索引为 1）
     */
    private final int index;
    /**
     * 背包容量
     */
    private final int bagWeight;
    /**
     * 背包价值
     */
    private final int bagValue;
    /**
     * 背包最优价值（上界）
     */
    private int upBound;

    public Node(int index, int bagWeight, int bagValue) {
        this.index = index;
        this.bagWeight = bagWeight;
        this.bagValue = bagValue;
    }

    public int getUpBound(int[][] nums, int capacity) {
        if (this.upBound > 0) {
            return this.upBound;
        }
        int newUpBound = this.bagValue;
        int bagLeft = capacity - bagWeight;
        int i = this.index;
        while (i < nums.length && bagLeft - nums[i][0] >= 0) {
            bagLeft -= nums[i][0];
            newUpBound += nums[i][1];
            i++;
        }

        // 背包未满，切割后放入
        if (i < nums.length) {
            newUpBound += 1.0 * bagLeft / nums[i][0] * nums[i][1];
        }

        return this.upBound = newUpBound;
    }

    @Override
    public int compareTo(Node o) {
        // 倒叙
        return o.upBound - this.upBound;
    }
}

整理完毕，完结撒花~ 🌻





参考地址：

1.算法分析与设计：分支限界法，https://blog.csdn.net/weixin_44712386/article/details/105532881

2.(五) 分支限界算法，https://www.jianshu.com/p/538e7612f68d

3.【算法】四、分支限界法，https://blog.csdn.net/m0_64403412/article/details/130694294

4.单源最短路径问题——分支限界法（Java），https://zhuanlan.zhihu.com/p/601400758

5.java 0-1背包问题 动态规划、回溯法、分支限界，https://blog.csdn.net/Dl_MrE/article/details/119572322

6.分支限界法求解0/1背包问题动画演示，https://www.bilibili.com/video/BV1gb411G7FH/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1295711.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SpringBoot系列之集成Jedis教程

SpringBoot系列之集成Jedis教程

SpringBoot系列之集成Jedis教程&#xff0c;Jedis是老牌的redis客户端框架&#xff0c;提供了比较齐全的redis使用命令&#xff0c;是一款开源的Java 客户端框架&#xff0c;本文使用Jedis3.1.0加上Springboot2.0&#xff0c;配合spring-boot-starter-data-redis使用&#xff0…
阅读更多...
【CVE 复现】CVE-2022-0185 fsconfig之整数溢出

【CVE 复现】CVE-2022-0185 fsconfig之整数溢出

影响版本&#xff1a;Linux-v5.1~v5.16.2 测试版本&#xff1a;Linux-5.11.22&#xff0c;由于懒得搞环境&#xff0c;所以直接用的 bsauce 大佬提供的 测试环境 看看 patch&#xff1a; diff --git a/fs/fs_context.c b/fs/fs_context.c index b7e43a780a625b..24ce12f0db32…
阅读更多...
Linux---日志管理

Linux---日志管理

本章主要介绍Linux中的日志管理 了解rsyslog是如何管理日志的查看日志的方法 日志管理简介 工作当中的日志&#xff0c;特指硬件和软件的日志&#xff0c;管理员可以通过它来检查错误发生的原因&#xff0c;或者寻找受到攻击时攻击者留下的痕迹。日志管理包括管理系统日志、应…
阅读更多...
三数组最小距离：2020年408算法题

三数组最小距离：2020年408算法题

算法思想 算法实现 #define INT_MAX 0x7fffffff //c语言int类型最大值 //计算绝对值 int abs(int a){if(a<0) return -a;else return a; } //判断a是否为3个数中最小值 bool isMin(int a,int b,int c){if(a<b&&a<c) return true;return false; }//主函数 in…
阅读更多...
SpringCloud 微服务集群升级记录（1.5.x-2.7.18）

SpringCloud 微服务集群升级记录（1.5.x-2.7.18）

前言 前段时间&#xff0c;因项目被扫出大量漏洞&#xff0c;全是因为依赖版本过低&#xff0c;存在高中危漏洞需要升级。正好本来也有规划集群升级&#xff0c;因为工作量大迟迟落实不了&#xff0c;正好有这次修漏洞的机会&#xff0c;升级微服务集群。这篇文章主要记录了本…
阅读更多...
案例053:基于微信小程序的乐室预约系统

案例053:基于微信小程序的乐室预约系统

文末获取源码 开发语言&#xff1a;Java 框架&#xff1a;SSM JDK版本&#xff1a;JDK1.8 数据库&#xff1a;mysql 5.7 开发软件&#xff1a;eclipse/myeclipse/idea Maven包&#xff1a;Maven3.5.4 小程序框架&#xff1a;uniapp 小程序开发软件&#xff1a;HBuilder X 小程序…
阅读更多...
如何快速完成企业私有云部署

如何快速完成企业私有云部署

快解析赋能企业私有云部署 ​ 很多企业形成了以总部为中心的多点生产体系结构&#xff0c;并借助网络化办公工具搭建跨区域协同办公系统&#xff0c;满足总部与分支机构间的信息互通&#xff0c;进而促进异地业务的信息共享&#xff0c;提高办公处理效率和综合管理水平。 北…
阅读更多...
redis-学习笔记(string)

redis-学习笔记(string)

redis 中的字符串, 是按照二进制的方式存储和读取的, 即存啥取啥, 所以一般不会出现乱码问题 (乱码问题是因为存储和读取时使用的编码方式不一样, 但是 redis 没有编码转换) redis 限制了 string 的大小 : 512M, 因为 单线程模型 希望进行的操作能够比较快速, 越大越慢 set key…
阅读更多...
基于Java技术的选课管理系统设计与实现

基于Java技术的选课管理系统设计与实现

末尾获取源码 开发语言&#xff1a;Java Java开发工具&#xff1a;JDK1.8 后端框架&#xff1a;SSM 前端&#xff1a;采用JSP技术开发 数据库&#xff1a;MySQL5.7和Navicat管理工具结合 服务器&#xff1a;Tomcat8.5 开发软件&#xff1a;IDEA / Eclipse 是否Maven项目&#x…
阅读更多...
uniapp实战 —— 弹出层 uni-popup (含vue3子组件调父组件的方法)

uniapp实战 —— 弹出层 uni-popup (含vue3子组件调父组件的方法)

效果预览 弹出的内容 src\pages\goods\components\ServicePanel.vue <script setup lang"ts"> // 子组件调父组件的方法 const emit defineEmits<{(event: close): void }>() </script><template><view class"service-panel"…
阅读更多...
uniapp-实现一级二级职位选择，完整页面！！！

uniapp-实现一级二级职位选择，完整页面！！！

一、需求 该页面实现的功能有&#xff1a; 该页面是左侧为一级&#xff0c;右侧为二级&#xff1b;可以搜索职位进行选择&#xff1b;底部显示已选的岗位&#xff0c;点击每一项会删除&#xff1b;右侧的二级岗位&#xff0c;点击时会选中&#xff0c;再次点击会取消&#xf…
阅读更多...
Qt 5.15.2 三维显示功能

Qt 5.15.2 三维显示功能

Qt 5.15.2 三维显示功能 三维显示效果&#xff1a; .pro项目文件 QT core gui opengl 3dcore 3drender 3dinput 3dextrasgreaterThan(QT_MAJOR_VERSION, 4): QT widgetsCONFIG c17# You can make your code fail to compile if it uses deprecated APIs. # In ord…
阅读更多...
“我要报名”参观双十二外贸电商节，报名方式都在这！

“我要报名”参观双十二外贸电商节，报名方式都在这！

双十二外贸电商节深圳进出口贸易博览会 2023年12月11-12日 深圳福田会展中心 近1万方展览面积 30000专业观众 跨境选品 外贸采购 行业趋势 人才对接 ▼▼▼▼ 展会时间 2023年12月11日-12日 展会地点 深圳福田会展中心 双十二外贸电商节暨2023深圳进出口贸易博览会选…
阅读更多...
更多内窥镜维修技能学习与交流可关注西安彩虹

更多内窥镜维修技能学习与交流可关注西安彩虹

内窥镜结构及光学成像原理 众多品牌的硬镜其内部结构基本相似&#xff08;如下图&#xff09;&#xff0c;最关键的在于不同用途的硬镜在其结构上发生变化&#xff0c;包括光学成像系统和机械结构。光学成像系统由物镜系统、转像系统、目镜系统三大系统组成。 工作原理 被观察…
阅读更多...
发布“最强”AI大模型，股价大涨，吊打GPT4的谷歌股票值得投资吗？

发布“最强”AI大模型，股价大涨，吊打GPT4的谷歌股票值得投资吗？

来源&#xff1a;猛兽财经 作者&#xff1a;猛兽财经 谷歌在AI领域的最新进展&#xff0c;引发投资者关注 在谷歌-C(GOOGL)谷歌-A&#xff08;GOOG&#xff09;昨日发布了最新的AI大模型Gemini后&#xff0c;其股价就出现了大幅上涨&#xff0c;更是引发了投资者的密切关注&a…
阅读更多...
将输入的字符串反向输出(c语言)

将输入的字符串反向输出(c语言)

#include<stdio.h> #include<string.h> int main() {int i, j, k;char s[50], temp;gets(s);//输入k strlen(s);//计算字符的长度//反向输出for (i 0, j k - 1;i < k / 2;i, j--){temp s[i];s[i] s[j];s[j] temp;}puts(s);//输出 }
阅读更多...
Ubuntu22.04安装和卸载软件的命令行

Ubuntu22.04安装和卸载软件的命令行

一、安装 sudo apt install xxx 二、卸载 sudo apt remove xxx 三、卸载依赖包(可选) 第二步软件卸载之后&#xff0c;有一些依赖包没有被卸载。可以使用sudo apt autoremove xxx来卸载。如果不卸载应该也没什么影响
阅读更多...
数据结构线性表-栈和队列的实现

数据结构线性表-栈和队列的实现

1. 栈(Stack) 1.1 概念 栈&#xff1a;一种特殊的线性表&#xff0c;其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈 顶&#xff0c;另一端称为栈底。栈中的数据元素遵守后进先出LIFO&#xff08;Last In First Out&#xff09;的原则。 …
阅读更多...
周星驰 互联网3.0 团队下个月将上线独立 App

周星驰 互联网3.0 团队下个月将上线独立 App

2023年12月7日&#xff0c;新浪科技报道指出&#xff0c;周星驰旗下的互联网3.0团队透露&#xff0c;Moonbox&#xff0c;这家周星驰创立的互联网3.0初创公司&#xff0c;计划在明年1月份完成Moonbox App的上线&#xff0c;届时该应用将免费向用户提供服务。 目前&#xff0c;…
阅读更多...
进制 + 原码，反码，补码

进制 + 原码，反码，补码

进制转换 整数部分 小数部分 原码 反码 补码 原码转补码&#xff1a; 左边和右边第一个1不变&#xff0c;中间取反。-0 除外。 计算机系统中数值一律用补码来存储的原因 其他 术语 进制表 进制数的表示 详细教程可转 爱编程的大丙
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023