一、题目大意
我们有N只猫,每次循环进行K次操作(N<=100,K<=100),每次操作可有以下三种选择:
1、g i 给第i只猫1个食物
2、e i 让第i只猫吃完它所有的食物
3、s i j 交换第i和j只猫的食物。
求出M次循环后,每只猫有多少个食物?(M<=1000000000)
二、解题思路
假设已经循环过 w 次,设第i只猫的食物数量为 ai
设循环过 w+1 次,第 i 只猫的食物数量为 bi。
不难1次循环的k个操作后,bi = a1 * m1 + a2 * m2 + a3 * m3 + ... an * mn + C
所以可推出以下的矩阵成立
同时当 ai 和 bi 之间相差M次循环时,也有如下表达式成立。
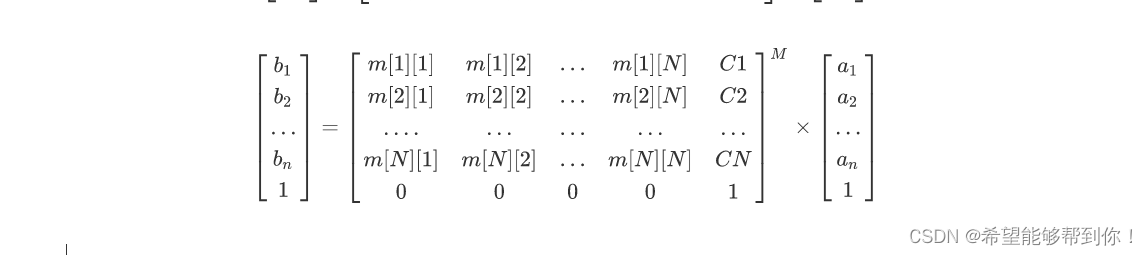
考虑下初始的情况,一开始每只猫都没有食物,设 Si 为 M次循环后第 i 只猫的数量,把初值代入 a1 .. an,有如下表达式成立。

但是这样我们需要使用 101 * 101大小的矩阵进行相乘,而且本题目需要开long long。
但经过思考,发现可以把矩阵降低一维成为100。
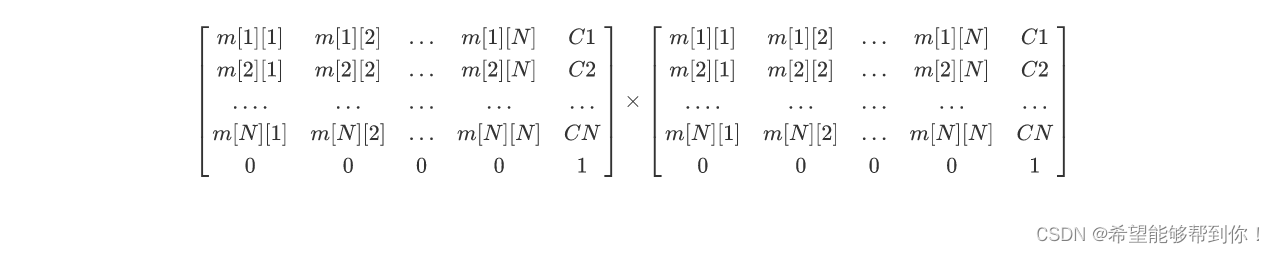
我们可以发现矩阵M次方的规律。
1、 对于矩阵中 1 <= 1 <= N,我们发现 这些值不管成多少次,都与第M+1行和N+1列无关。
2、最后一行始终不变。
3、对于最后一列,我们发现它可以通过如下表
达式。在100 * 100的复杂性内计算。
设进行经过i次循环的最后一列为Ci。对于最后一列的第 j 行则有如下表达式。
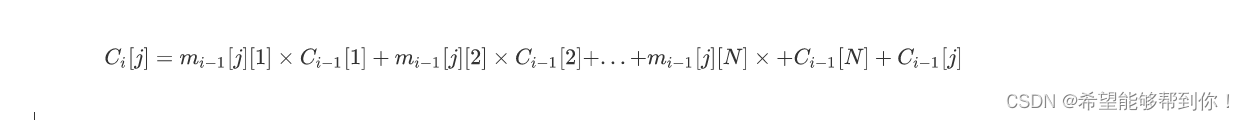
维护4个滑动数组,计算每一次更新内圈的后,再更新最后一列的值,M次操作后,最后一列的值就是答案,因为M次次幂即可求解答案。(初始时每只小鼠没有食物,最一列开long long,中间开int即可)。
三、代码
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
int P[2][107][107], B[107][107];
ll _P[2][107], _B[107];
int N, M, K;
void pow(int _N)
{
int cnt = 0;
while (_N > 0)
{
int crt = cnt & 1, nxt = !(cnt & 1);
if (_N & 1)
{
for (int i = 0; i < N; i++)
{
_P[nxt][i] = _B[i];
for (int j = 0; j < N; j++)
{
_P[nxt][i] = _P[nxt][i] + ((ll)B[i][j]) * _P[crt][j];
P[nxt][i][j] = 0;
for (int k = 0; k < N; k++)
{
P[nxt][i][j] = P[nxt][i][j] + B[i][k] * P[crt][k][j];
}
}
}
for (int i = 0; i < N; i++)
{
_B[i] = _P[nxt][i];
for (int j = 0; j < N; j++)
{
B[i][j] = P[nxt][i][j];
}
}
}
for (int i = 0; i < N; i++)
{
_P[nxt][i] = _P[crt][i];
for (int j = 0; j < N; j++)
{
_P[nxt][i] = _P[nxt][i] + ((ll)P[crt][i][j]) * _P[crt][j];
P[nxt][i][j] = 0;
for (int k = 0; k < N; k++)
{
P[nxt][i][j] = P[nxt][i][j] + P[crt][i][k] * P[crt][k][j];
}
}
}
cnt++;
_N >>= 1;
}
}
void solve()
{
for (int i = 0; i < 101; i++)
{
for (int j = 0; j < 101; j++)
{
B[i][j] = P[0][i][j] = P[1][i][j] = 0;
}
B[i][i] = 1;
P[0][i][i] = 1;
_P[0][i] = 0;
_B[i] = 0;
}
char c;
int a, b;
for (int i = 0; i < K; i++)
{
scanf("\n%c", &c);
if (c == 'g')
{
scanf("%d", &a);
_P[0][a - 1]++;
}
else if (c == 's')
{
scanf("%d%d", &a, &b);
for (int j = 0; j < N; j++)
{
int tmp = P[0][a - 1][j];
P[0][a - 1][j] = P[0][b - 1][j];
P[0][b - 1][j] = tmp;
}
ll tmpL = _P[0][a - 1];
_P[0][a - 1] = _P[0][b - 1];
_P[0][b - 1] = tmpL;
}
else if (c == 'e')
{
scanf("%d", &a);
for (int j = 0; j < N; j++)
{
P[0][a - 1][j] = 0;
}
_P[0][a - 1] = 0;
}
}
pow(M);
for (int i = 0; i < N; i++)
{
printf("%lld%c", _B[i], i + 1 == N ? '\n' : ' ');
}
}
int main()
{
while (true)
{
scanf("%d%d%d", &N, &M, &K);
if (N == 0 && M == 0 && K == 0)
{
break;
}
solve();
}
return 0;
}



![[oeasy]python0002_终端_CLI_GUI_编程环境_游戏_真实_元宇宙](https://img-blog.csdnimg.cn/img_convert/79e41e0fe5ec211694f8bb3bc9455fbb.png)