中缀表达式转后缀表达式与后缀表达式计算（详解）

**中缀表达式转后缀表达式的一般步骤如下：
1：创建一个空的栈和一个空的输出列表。
2：从左到右扫描中缀表达式的每个字符。
3：如果当前字符是操作数，则直接将其加入到输出列表中。
4：如果当前字符是运算符，比较其与栈顶运算符的优先级：

a. 如果栈为空或栈顶运算符是左括号"(“，则直接将当前运算符入栈。
b. 如果当前运算符的优先级高于栈顶运算符的优先级，则将当前运算符入栈。
c. 如果当前运算符的优先级低于或等于栈顶运算符的优先级，则将栈顶运算符弹出并加入到输出列表中，
直到栈为空或栈顶运算符的优先级低于当前运算符的优先级，然后将当前运算符入栈。
d. 如果当前字符是右括号”)“，则依次弹出栈中的运算符并加入到输出列表中，
直到遇到左括号”("为止，此时将左括号出栈且不加入输出列表。

5：扫描完整个中缀表达式后，将栈中剩余的运算符依次弹出并加入到输出列表中。
6：输出列表即为转换后的后缀表达式。
举个例子：
中缀表达式：2 + 3 * (4 - 1)
转换为后缀表达式：2 3 4 1 - * +
具体实现需要根据编程语言和数据结构来进行操作。**

项目结构
在这里插入图片描述 项目头文件结构QueueStorage.h
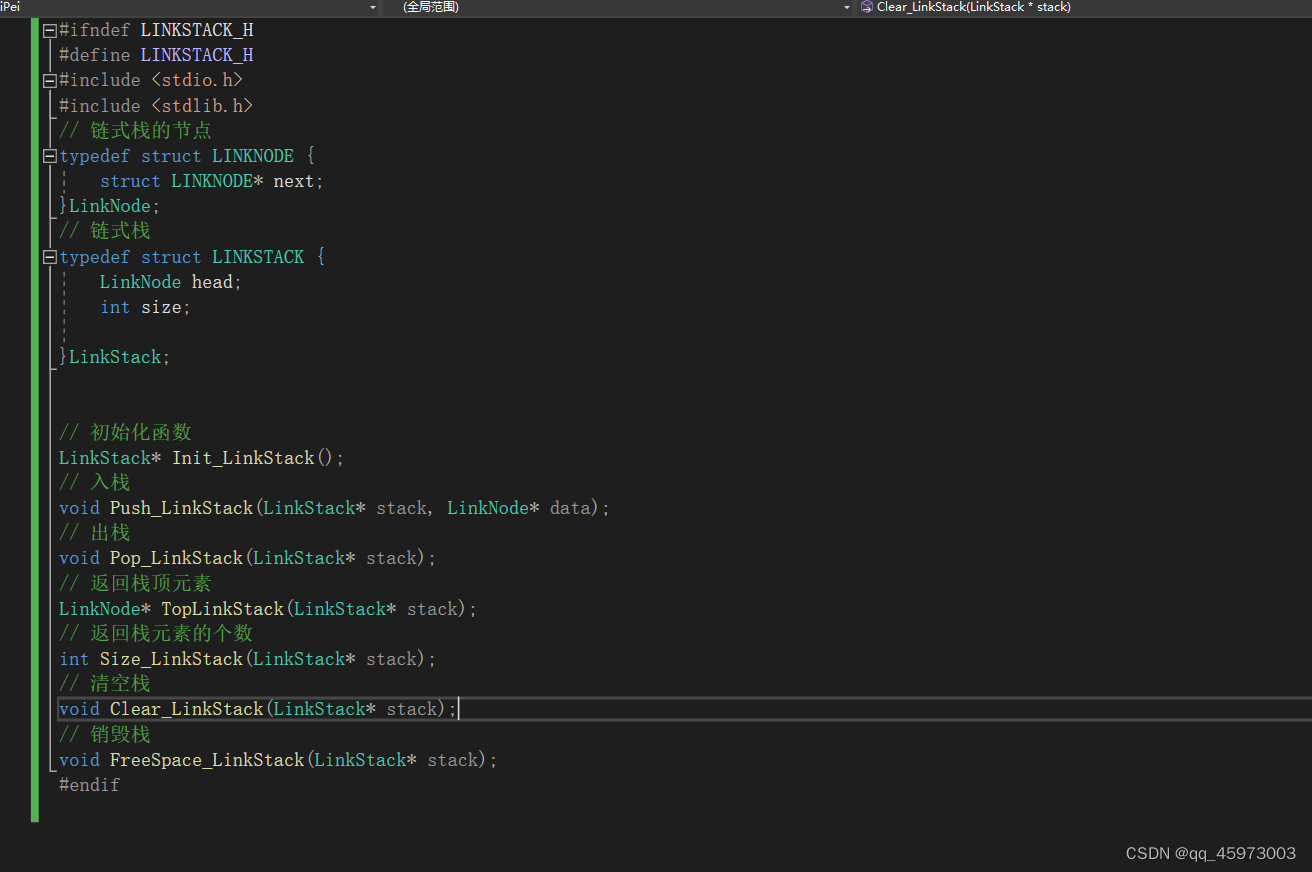项目头文件代码

#ifndef LINKSTACK_H
#define LINKSTACK_H
#include <stdio.h>
#include <stdlib.h>
// 链式栈的节点
typedef struct LINKNODE {
	struct LINKNODE* next;
}LinkNode;
// 链式栈
typedef struct LINKSTACK {
	LinkNode head;
	int size;

}LinkStack;


// 初始化函数
LinkStack* Init_LinkStack();
// 入栈
void Push_LinkStack(LinkStack* stack, LinkNode* data);
// 出栈
void Pop_LinkStack(LinkStack* stack);
// 返回栈顶元素
LinkNode* TopLinkStack(LinkStack* stack);
// 返回栈元素的个数
int Size_LinkStack(LinkStack* stack);
// 清空栈
void Clear_LinkStack(LinkStack* stack);
// 销毁栈
void FreeSpace_LinkStack(LinkStack* stack);
#endif

项目cpp文件QueueStorage.cpp
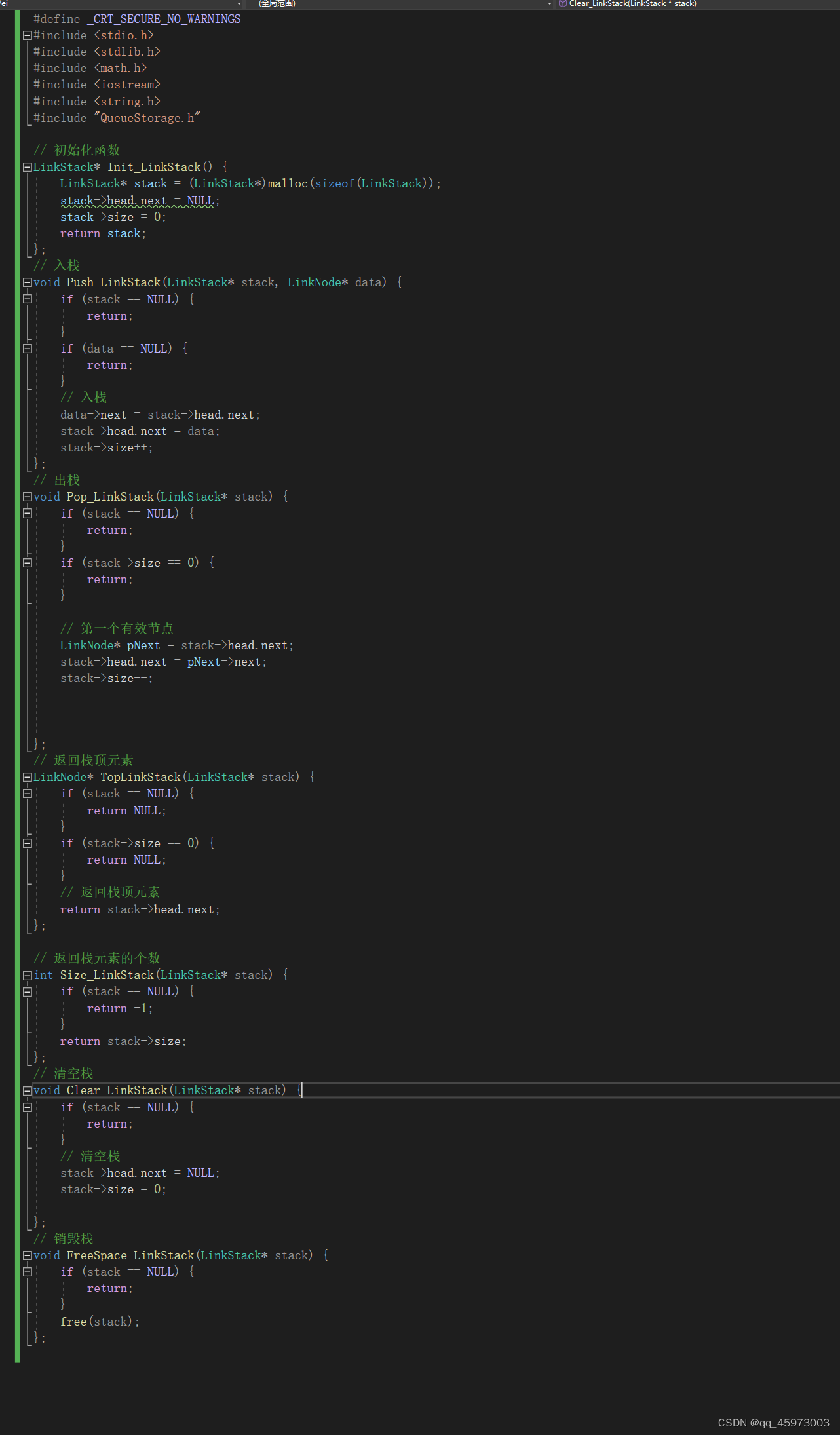在这里插入图片描述 项目cpp文件代码QueueStorage.cpp

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <iostream>
#include <string.h>
#include "QueueStorage.h"

// 初始化函数
LinkStack* Init_LinkStack() {
    LinkStack* stack = (LinkStack*)malloc(sizeof(LinkStack));
    stack->head.next = NULL;
    stack->size = 0;
    return stack;
};
// 入栈
void Push_LinkStack(LinkStack* stack, LinkNode* data) {
    if (stack == NULL) {
        return;
    }
    if (data == NULL) {
        return;
    }
    // 入栈
    data->next = stack->head.next;
    stack->head.next = data;
    stack->size++;
};
// 出栈
void Pop_LinkStack(LinkStack* stack) {
    if (stack == NULL) {
        return;
    }
    if (stack->size == 0) {
        return;
    }

    // 第一个有效节点
    LinkNode* pNext = stack->head.next;
    stack->head.next = pNext->next;
    stack->size--;



};
// 返回栈顶元素
LinkNode* TopLinkStack(LinkStack* stack) {
    if (stack == NULL) {
        return NULL;
    }
    if (stack->size == 0) {
        return NULL;
    }
    // 返回栈顶元素
    return stack->head.next;
};

// 返回栈元素的个数
int Size_LinkStack(LinkStack* stack) {
    if (stack == NULL) {
        return -1;
    }
    return stack->size;
};
// 清空栈
void Clear_LinkStack(LinkStack* stack) {
    if (stack == NULL) {
        return;
    }
    // 清空栈
    stack->head.next = NULL;
    stack->size = 0;

};
// 销毁栈
void FreeSpace_LinkStack(LinkStack* stack) {
    if (stack == NULL) {
        return;
    }
    free(stack);
};

项目主文件截图
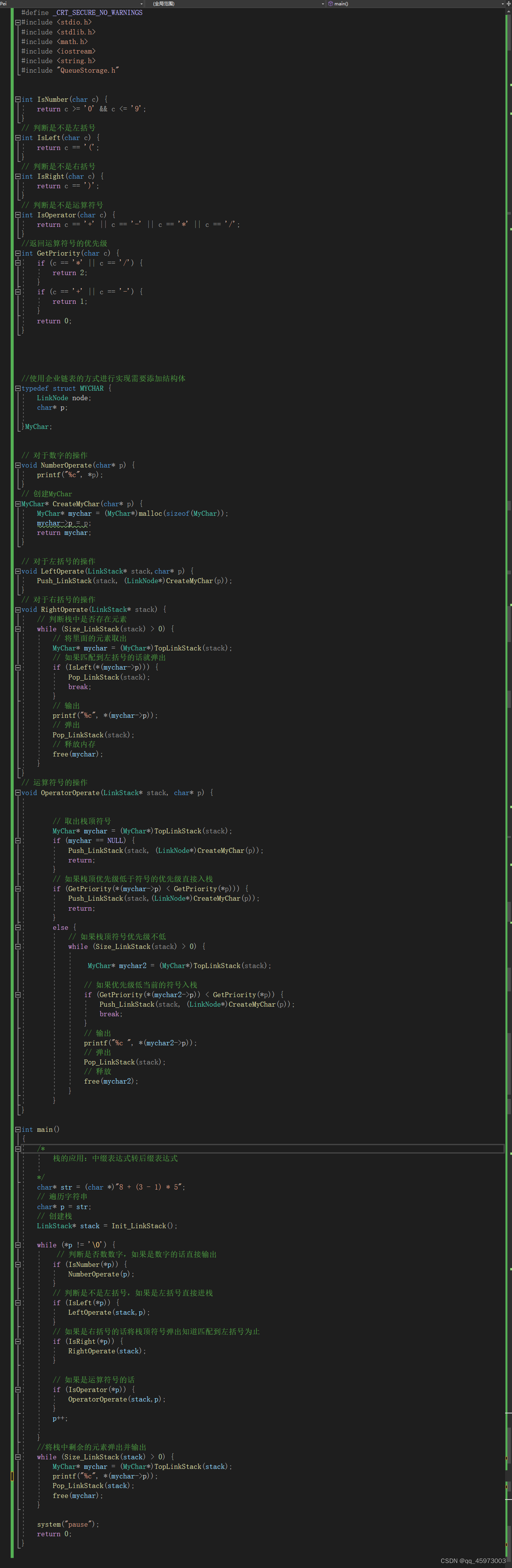在这里插入图片描述 项目主文件代码main.cpp

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <iostream>
#include <string.h>
#include "QueueStorage.h"


int IsNumber(char c) {
	return c >= '0' && c <= '9';
}
// 判断是不是左括号
int IsLeft(char c) {
	return c == '(';
}
// 判断是不是右括号
int IsRight(char c) {
	return c == ')';
}
// 判断是不是运算符号
int IsOperator(char c) {
	return c == '+' || c == '-' || c == '*' || c == '/';
}
//返回运算符号的优先级
int GetPriority(char c) {
	if (c == '*' || c == '/') {
		return 2;
	}
	if (c == '+' || c == '-') {
		return 1;
	}
	return 0;
}




//使用企业链表的方式进行实现需要添加结构体
typedef struct MYCHAR {
	LinkNode node;
	char* p;

}MyChar;


// 对于数字的操作
void NumberOperate(char* p) {
	printf("%c", *p);
}
// 创建MyChar
MyChar* CreateMyChar(char* p) {
	MyChar* mychar = (MyChar*)malloc(sizeof(MyChar));
	mychar->p = p;
	return mychar;
}

// 对于左括号的操作
void LeftOperate(LinkStack* stack,char* p) {
	Push_LinkStack(stack, (LinkNode*)CreateMyChar(p));
}
// 对于右括号的操作
void RightOperate(LinkStack* stack) {
	// 判断栈中是否存在元素
	while (Size_LinkStack(stack) > 0) {
		// 将里面的元素取出
		MyChar* mychar = (MyChar*)TopLinkStack(stack);
		// 如果匹配到左括号的话就弹出
		if (IsLeft(*(mychar->p))) {
			Pop_LinkStack(stack);
			break;
		}
		// 输出
		printf("%c", *(mychar->p));
		// 弹出
		Pop_LinkStack(stack);
		// 释放内存
		free(mychar);
	}
}
// 运算符号的操作
void OperatorOperate(LinkStack* stack, char* p) {
		

		// 取出栈顶符号
		MyChar* mychar = (MyChar*)TopLinkStack(stack);
		if (mychar == NULL) {
			Push_LinkStack(stack, (LinkNode*)CreateMyChar(p));
			return;
		}
		// 如果栈顶优先级低于符号的优先级直接入栈
		if (GetPriority(*(mychar->p) < GetPriority(*p))) {
			Push_LinkStack(stack,(LinkNode*)CreateMyChar(p));
			return;
		}
		else {
			// 如果栈顶符号优先级不低
			while (Size_LinkStack(stack) > 0) {

				 MyChar* mychar2 = (MyChar*)TopLinkStack(stack);

				// 如果优先级低当前的符号入栈
				if (GetPriority(*(mychar2->p)) < GetPriority(*p)) {
					Push_LinkStack(stack, (LinkNode*)CreateMyChar(p));
					break;
				}
				// 输出
				printf("%c ", *(mychar2->p));
				// 弹出
				Pop_LinkStack(stack);
				// 释放
				free(mychar2);
			}
		}
}

int main()
{
	/*
	    栈的应用：中缀表达式转后缀表达式

	*/
	char* str = (char *)"8 + (3 - 1) * 5";
	// 遍历字符串
	char* p = str;
	// 创建栈
	LinkStack* stack = Init_LinkStack();

	while (*p != '\0') {
	     // 判断是否数数字，如果是数字的话直接输出
		if (IsNumber(*p)) {
			NumberOperate(p);
		}
		// 判断是不是左括号，如果是左括号直接进栈
		if (IsLeft(*p)) {
			LeftOperate(stack,p);
		}
		// 如果是右括号的话将栈顶符号弹出知道匹配到左括号为止
		if (IsRight(*p)) {
			RightOperate(stack);
		}

		// 如果是运算符号的话
		if (IsOperator(*p)) {
			OperatorOperate(stack,p);
		}
		p++;
		
	}
	//将栈中剩余的元素弹出并输出
	while (Size_LinkStack(stack) > 0) {
		MyChar* mychar = (MyChar*)TopLinkStack(stack);
		printf("%c", *(mychar->p));
		Pop_LinkStack(stack);
		free(mychar);
	}

	system("pause");
	return 0;
}

修改运行界面
在这里插入图片描述 项目运行结果

在这里插入图片描述
后缀表达式相关原理

在这里插入图片描述 计算这个后缀表达式"2 3 4 1 - * +"。**

首先，我们从左到右扫描后缀表达式，遇到数字就将其入栈，遇到运算符则将栈顶的两个数字弹出进行计算，然后将结果入栈。
具体计算过程如下：

将2和3入栈
遇到4，入栈
遇到1，入栈
遇到减号"-"，弹出栈顶两个数字1和4，计算4-1=3，将结果3入栈
遇到乘号""，弹出栈顶两个数字3和3，计算33=9，将结果9入栈
遇到加号"+"，弹出栈顶两个数字9和2，计算9+2=11，将结果11入栈
后缀表达式扫描结束，栈顶的数字11即为最终的计算结果。

主文件
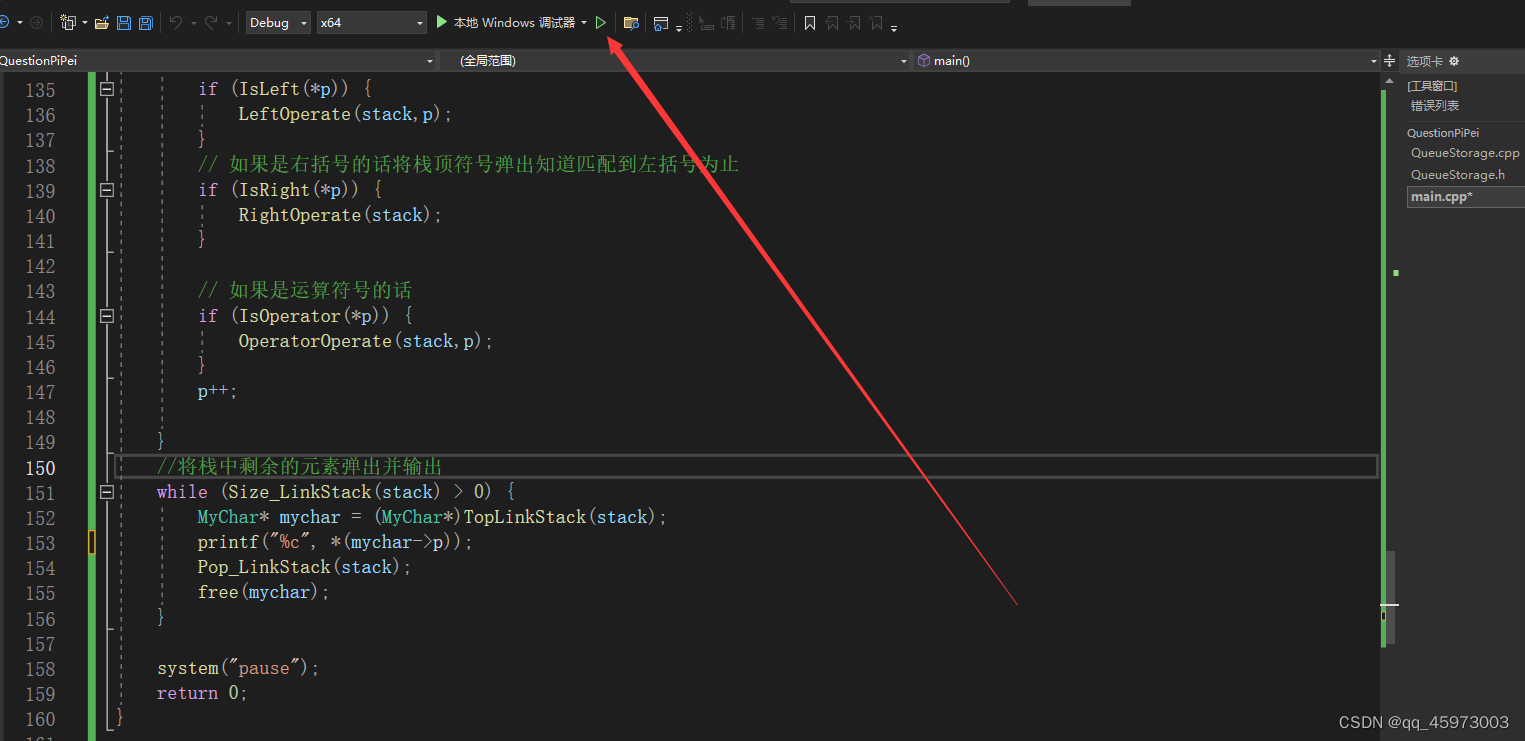
在这里插入图片描述
主文件截图
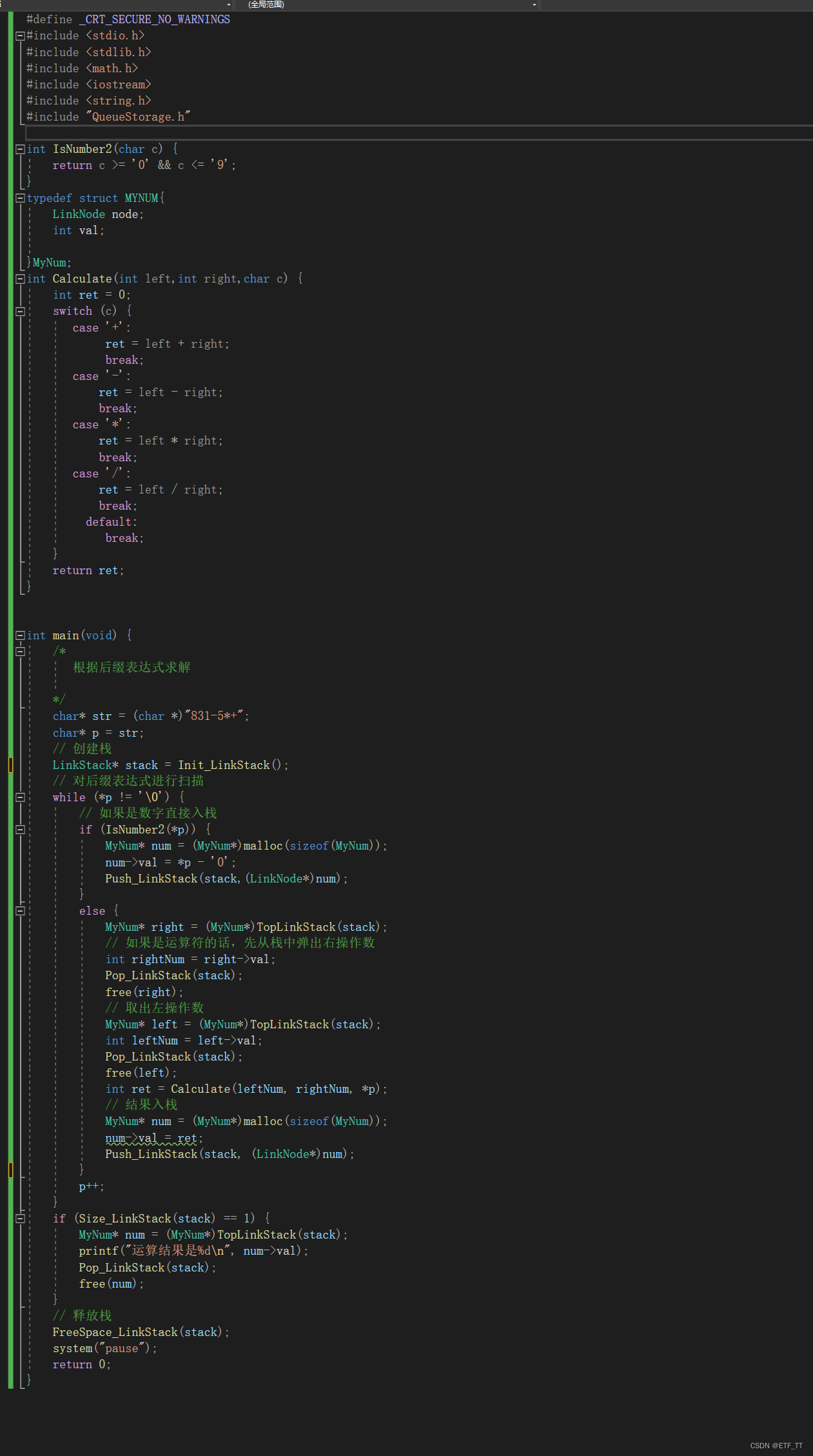主文件代码

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <iostream>
#include <string.h>
#include "QueueStorage.h"

int IsNumber2(char c) {
    return c >= '0' && c <= '9';
}
typedef struct MYNUM{
    LinkNode node;
    int val;

}MyNum;
int Calculate(int left,int right,char c) {
    int ret = 0;
    switch (c) {
       case '+':
            ret = left + right;
            break;
       case '-':
           ret = left - right;
           break;
       case '*':
           ret = left * right;
           break;
       case '/':
           ret = left / right;
           break;
         default:
            break;
    }
    return ret;
}


int main(void) {
    /*
       根据后缀表达式求解

    */
    char* str = (char *)"831-5*+";
    char* p = str;
    // 创建栈
    LinkStack* stack = Init_LinkStack();
    // 对后缀表达式进行扫描
    while (*p != '\0') {
        // 如果是数字直接入栈
        if (IsNumber2(*p)) {
            MyNum* num = (MyNum*)malloc(sizeof(MyNum));
            num->val = *p - '0';
            Push_LinkStack(stack,(LinkNode*)num);
        }
        else {
            MyNum* right = (MyNum*)TopLinkStack(stack);
            // 如果是运算符的话，先从栈中弹出右操作数
            int rightNum = right->val;
            Pop_LinkStack(stack);
            free(right);
            // 取出左操作数
            MyNum* left = (MyNum*)TopLinkStack(stack);
            int leftNum = left->val;
            Pop_LinkStack(stack);
            free(left);
            int ret = Calculate(leftNum, rightNum, *p);
            // 结果入栈
            MyNum* num = (MyNum*)malloc(sizeof(MyNum));
            num->val = ret;
            Push_LinkStack(stack, (LinkNode*)num);
        }
        p++;
    }
    if (Size_LinkStack(stack) == 1) {
        MyNum* num = (MyNum*)TopLinkStack(stack);
        printf("运算结果是%d\n", num->val);
        Pop_LinkStack(stack);
        free(num);
    }
    // 释放栈
    FreeSpace_LinkStack(stack);
    system("pause");
    return 0;
}