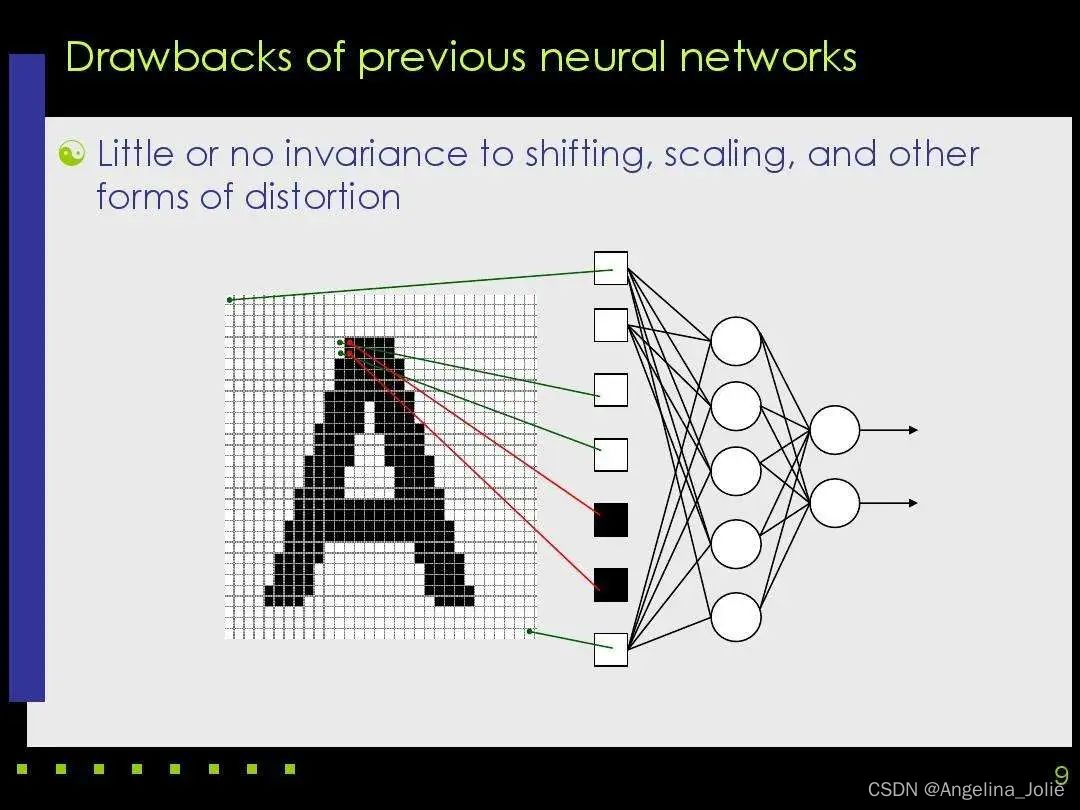
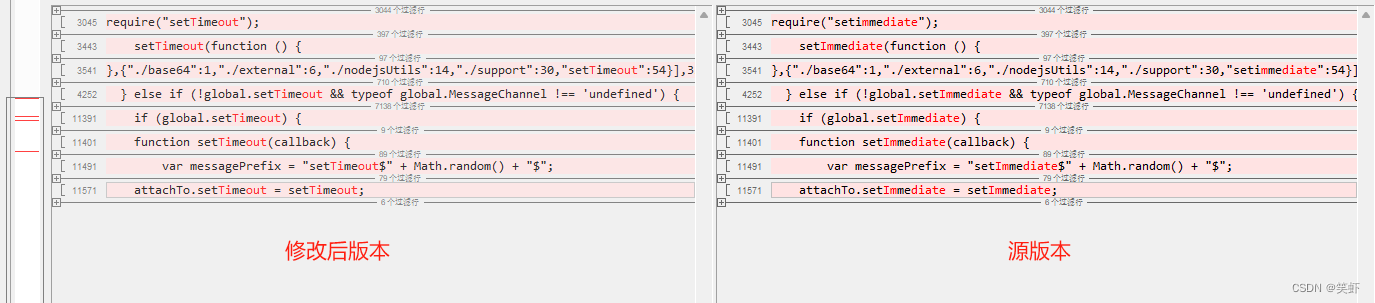
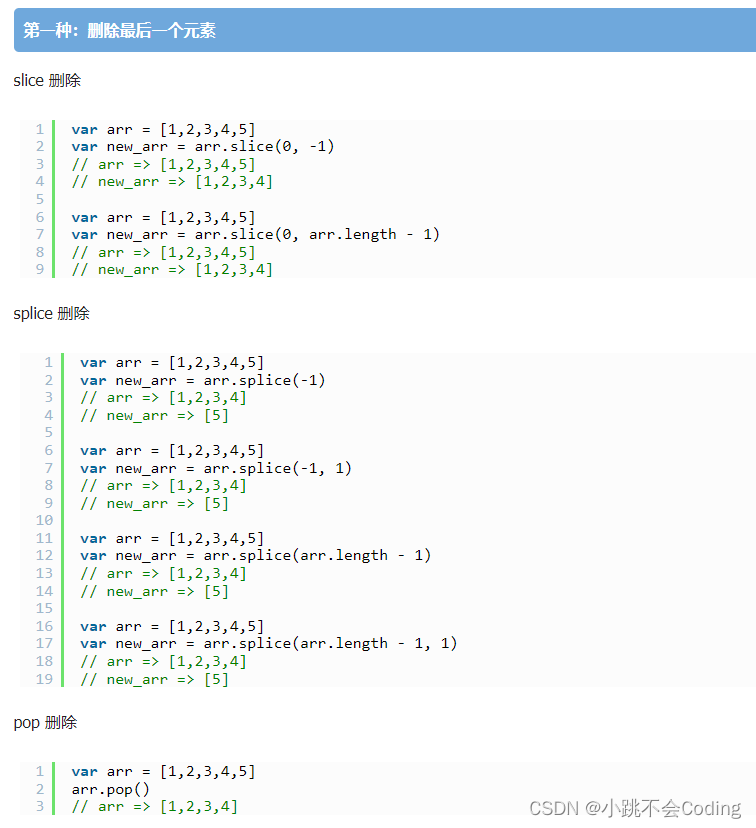
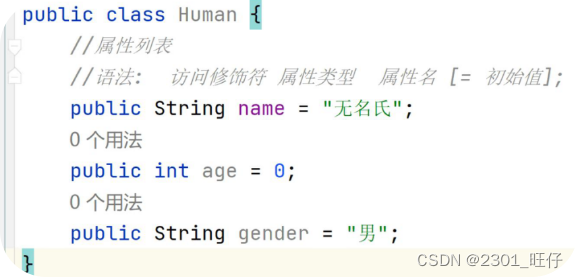
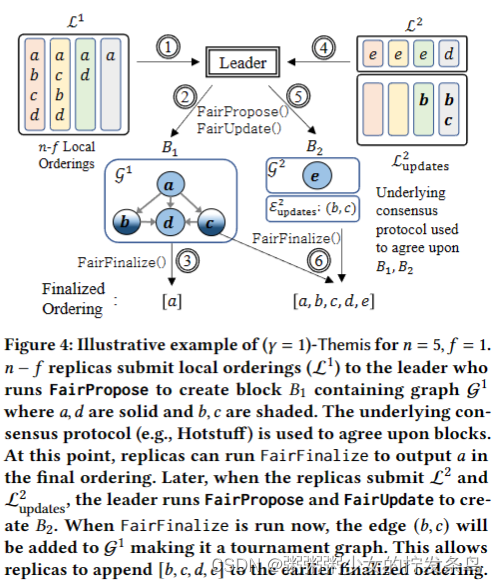
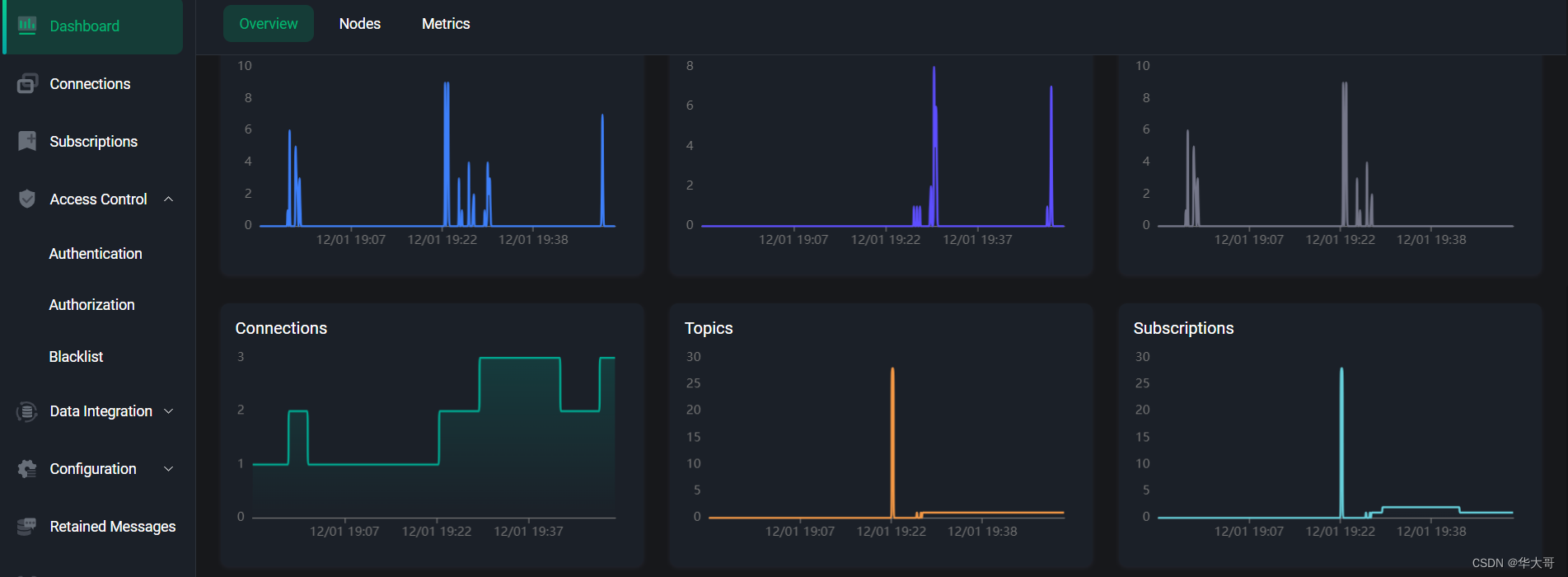
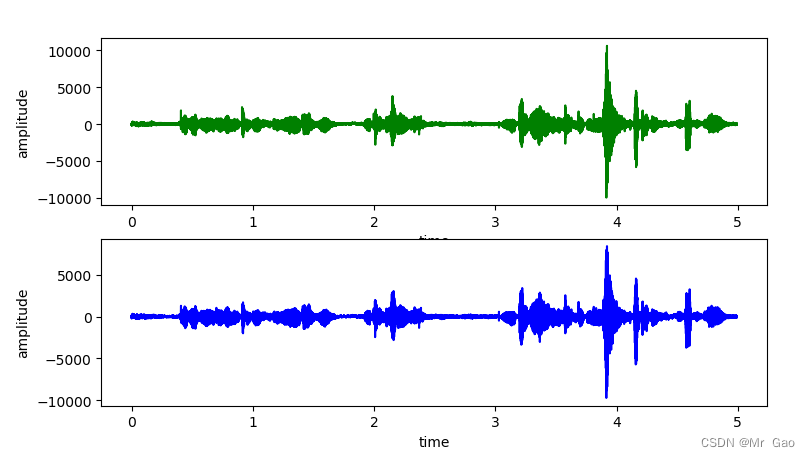
一、来源：[1312.4400] Network In Network （如果1×1卷积核接在普通的卷积层后面，配合激活函数，即可实现network in network的结构）

二、应用：GoogleNet中的Inception、ResNet中的残差模块

三、作用：

1、降维（减少参数）

例子1 : GoogleNet中的3a模块

输入的feature map是28×28×192

1×1卷积通道为64

3×3卷积通道为128

5×5卷积通道为32

左图卷积核参数：192 × (1×1×64) +192 × (3×3×128) + 192 × (5×5×32) = 387072

右图对3×3和5×5卷积层前分别加入了通道数为96和16的1×1卷积层，这样卷积核参数就变成了:

192 × (1×1×64) +（192×1×1×96+ 96 × 3×3×128）+（192×1×1×16+16×5×5×32）= 157184

同时在并行pooling层后面加入1×1卷积层后也可以降低输出的feature map数量（feature map尺寸指W、H是共享权值的sliding window，feature map 的数量就是channels）

左图feature map数量：64 + 128 + 32 + 192(pooling后feature map不变) = 416 （如果每个模块都这样，网络的输出会越来越大）

右图feature map数量：64 + 128 + 32 + 32(pooling后面加了通道为32的1×1卷积) = 256

GoogLeNet利用1×1的卷积降维后，得到了更为紧凑的网络结构，虽然总共有22层，但是参数数量却只是8层的AlexNet的十二分之一（当然也有很大一部分原因是去掉了全连接层）

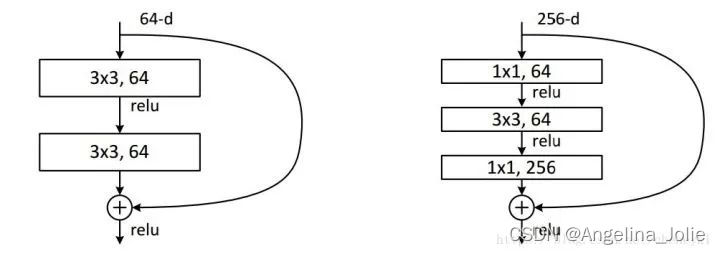
例子2：ResNet中的残差模块

假设上一层的feature map是w*h*256,并且最后要输出的是256个feature map

左侧操作数：w*h*256*3*3*256 =589824*w*h

右侧操作数：w*h*256*1*1*64 + w*h*64*3*3*64 +w*h*64*1*1*256 = 69632*w*h,，左侧参数大概是右侧的8.5倍。（实现降维，减少参数）

2、升维（用最少的参数拓宽网络channal）

例子：上一个例子中，不仅在输入处有一个1*1卷积核，在输出处也有一个卷积核，3*3，64的卷积核的channel是64，只需添加一个1*1，256的卷积核，只用64*256个参数就能把网络channel从64拓宽四倍到256。

3、跨通道信息交互（channal 的变换）

例子：使用1*1卷积核，实现降维和升维的操作其实就是channel间信息的线性组合变化，3*3，64channels的卷积核后面添加一个1*1，28channels的卷积核，就变成了3*3，28channels的卷积核，原来的64个channels就可以理解为跨通道线性组合变成了28channels，这就是通道间的信息交互。

注意：只是在channel维度上做线性组合，W和H上是共享权值的sliding window

4、增加非线性特性

1*1卷积核，可以在保持feature map尺度不变的（即不损失分辨率）的前提下大幅增加非线性特性（利用后接的非线性激活函数），把网络做的很deep。

备注：一个filter对应卷积后得到一个feature map，不同的filter(不同的weight和bias)，卷积以后得到不同的feature map，提取不同的特征，得到对应的specialized neuro。

四、从fully-connected layers的角度来理解1*1卷积核

将其看成全连接层

左边6个神经元，分别是a1—a6，通过全连接之后变成5个，分别是b1—b5

左边6个神经元相当于输入特征里面的channels：6

右边5个神经元相当于1*1卷积之后的新的特征channels：5

左边 W*H*6 经过 1*1*5的卷积核就能实现全连接。

In Convolutional Nets, there is no such thing as “fully-connected layers”. There are only convolution layers with 1x1 convolution kernels and a full connection table– Yann LeCun

参考：https://iamaaditya.github.io/2016/03/one-by-one-convolution/