目录
- 问题一
- 问题二
- 问题三
- 问题四
本讲为考前复习课,考试范围就是 Ax=b 这个单元,重点是长方形矩阵,与此相关的概念包括零空间、左零空间、秩、向量空间、子空间,特别是四个基本子空间。当矩阵为可逆的方阵时,很多性质是一目了然的,但是对于长方形矩阵则需要多加注意。
问题一
向量 u,v 和 w 是 R7空间中的非零向量。它们张成了 R7空间中的一个子空间,那么这个子空间的维数可能是多少?
解答:1,2 或者 3。空间的基的个数不超过 3 个,所以其维数也不会超过 3。因为是非零向量,所以不能是 0。
问题二
给定矩阵 U 为 5 X 3 阶梯型矩阵,其秩 r=3。
1.求 U 的零空间 N(U)
解答:因为列数为 3 且秩为 3,其列向量线性无关,则 Ux=0 只有零解,所以其零空间 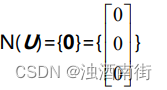

5.C 的秩?
解答:6,B 的秩为 3。
6.求 C 左零空间的维数 dim N(
C
T
C^T
CT)?
解答:m=10 而 r=6,所以 dim N(
C
T
C^T
CT)=4。
问题三
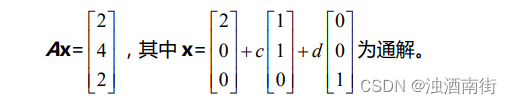
1.矩阵 A 的形状?
解答:矩阵 A 为 3 X 3 矩阵,因为 x 的分量数即为 A 的列数,而 b 的分量数为A 的行数。
2.矩阵 A 的行空间的维数?
解答:从通解的形式可以看出 A 零空间的维数为 2,则其行空间的维数为 3-2=1。

本题中矩阵的秩为 1,因此零空间很大。请注意系数矩阵满秩的情况,我们曾经花了不少时间进行讨论。
小问题
1.A 是方阵,零空间只有零向量 0,AT的零空间?
解答:AT的零空间也只有零向量。
2.所有的 5 X 5 可逆矩阵,是否构成 5 X 5 矩阵空间的子空间?
解答:不行,不包含零矩阵 0,不是子空间。顺便说一下奇异阵也不是一个子空间。

4.判断:方程组 Ax=b 具有 n 个方程 n 个未知数,若矩阵 A 的列向量线性无关,则b 取任意向量,方程均有解。
解答:是,A 为可逆矩阵,所以 x=
A
−
1
A^{-1}
A−1b 是唯一解。
问题四
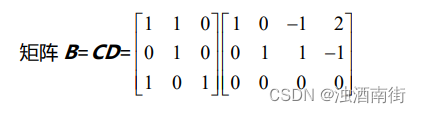
1.给出矩阵 B 零空间的一组基?
解答:因为矩阵 C 为可逆矩阵,因此矩阵 B 零空间与矩阵 D 的零空间相同。


小问题
1.判断:A 为方阵,则它的行空间和列空间相同?
解答:否,只是空间的维数相等,但空间不一定相同。反例
B
=
[
0
1
0
0
]
B=\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}
B=[0010]
2.判断:矩阵 A 和-A 的四个子空间相同?
解答:是,相同。
3.判断:如果 A 和 B 的四个子空间相同,则 A 一定是 B 的倍数?
解答:错误,A 和 B 的可以为同阶可逆方阵。
4.如果我们对矩阵 A 中的两行做行交换,四个子空间中不变的是哪些?
解答:是行空间和零空间。