C++新经典模板与泛型编程：策略技术中的算法策略

news2024/11/19 19:41:31

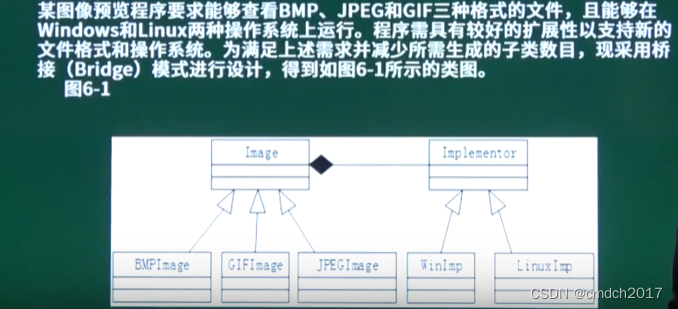
策略技术中的算法策略

  • 在之前博客中funcsum()函数模板中，实现了对数组元素的求和运算。求和在这里可以看作一种算法，扩展一下思路，对数组元素求差、求乘积、求最大值和最小值等，都可以看作算法。
  • 而当前的funcsum()函数模板中，已经将数组元素的求和算法固定写在了程序代码中，为了灵活地将求和算法调整为求乘积、求最大值等算法，可以通过引入一个策略（policy）类SumPolicy达到目的。
// 求和策略类以实现求和算法
struct SumPolicy
{
	// 静态成员函数模板
	template<typename sumT,typename T> // sumT是和值类型，T是数组元素类型
	static void algorithm(sumT& sum, const T& value) // 该策略类的核心算法
	{
		sum += value;
	}
};

接着，为funcsum()函数模板增加一个新的类型模板参数，这个模板参数的默认值就是这个策略类。
修改funcsum()函数模板：

template<typename T,typename U = SumFixedTraits<T>,typename V = SumPolicy>
auto funcsum(const T* begin, const T* end)
{
	typename U::sumT sum = U::initValue();

	for (;;)
	{
		// sum += (*begin); 此行被下面一行取代
		V::algorithm(sum, *begin);
		if (begin == end)
			break;
		++begin;
	}
	return sum;
}

如果要计算一个整型数组中元素的最小值，如何实现？第1件想到的事情就是写一个新的策略类，如这里写一个MinPolicy类（仿照SumPolicy类的写法）。

struct MinPolicy
{
	template<typename minT,typename T>
	static void algorithm(minT& min, const T& value)
	{
		if (min > value)
			min = value;
	}
};

在main()主函数中重新写入代码：

#include "killCmake.h"

#include<string>

using namespace std;

template<typename T>
struct SumFixedTraits;

template<>
struct SumFixedTraits<char>
{
	using sumT = int;
	static sumT initValue() {
		return 0;
	}
};

// 最求值策略技术时，为了求最小值，初始化需要很大
// 所以初始值可以为int最大值21亿
template<>
struct SumFixedTraits<int>
{
	using sumT = __int64;
	static sumT initValue() {
		return 2100000000;
	}
};

template<>
struct SumFixedTraits<double>
{
	using sumT = double;
	static sumT initValue() {
		return 0.0;
	}
};

template<typename T,typename U = SumFixedTraits<T>>
auto funcsum(const T* begin, const T* end)
{
	// using sumT = typename SumFixedTraits<T>::sumT;  本行不需要
	// sumT sum = SumFixedTraits<T>::initValue();  本行不需要
	typename U::sumT sum = U::initValue();

	for (;;)
	{
		sum += (*begin);
		if (begin == end)
			break;
		++begin;
	}
	return sum;
}

// 求和策略类以实现求和算法
struct SumPolicy
{
	// 静态成员函数模板
	template<typename sumT,typename T> // sumT是和值类型，T是数组元素类型
	static void algorithm(sumT& sum, const T& value) // 该策略类的核心算法
	{
		sum += value;
	}
};

template<typename T,typename U = SumFixedTraits<T>,typename V = SumPolicy>
auto funcsum(const T* begin, const T* end)
{
	typename U::sumT sum = U::initValue();

	for (;;)
	{
		// sum += (*begin); 此行被下面一行取代
		V::algorithm(sum, *begin);
		if (begin == end)
			break;
		++begin;
	}
	return sum;
}

struct MinPolicy
{
	template<typename minT,typename T>
	static void algorithm(minT& min, const T& value)
	{
		if (min > value)
			min = value;
	}
};




int main()
{
	//char my_char_array[] = "abc";
	//std::cout << (int)(funcsum(&my_char_array[0], &my_char_array[2])) << std::endl;

	//std::cout << (int)(funcsum<char, SumFixedTraits<int>>(&my_char_array[0], &my_char_array[2])) << std::endl;

	int my_int_array1[] = { 10,15,20 };
	std::cout << funcsum<int, SumFixedTraits<int>, MinPolicy>(&my_int_array1[0], &my_int_array1[2]) << std::endl;

	return 0;
}

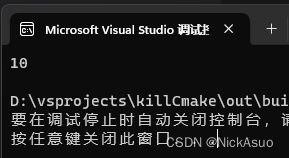
在这里插入图片描述
这个程序真的很经典，个人觉得，应该属于中上乘武功了

  • 运行程序，看一看新增的代码结果是否正确，最开始发现结果为0，显然这个结果是不正确的。究其原因，在funcsum()中，sum（用于保存数组元素最小值的变量）的初值被设置为0。如果是计算数组元素和值，则sum的初值被设置为0是很正常的；但如果要计算数组元素的最小值，则把sum的初值设置为0是不正常的（因为数组中元素的最小值也很可能比0大，有这个0存在，就无法找到数组中元素的真正最小值）。
  • 解决方案有以下两个。
  • （1）可以给funcsum()函数模板增加一个非类型模板参数，用于把初值传递进来。
  • （2）也可以重新写一个固定萃取类模板取代当前的SumFixedTraits模板。这里采用后一种解决方案，书写一个新的固定萃取类模板，取名为MinFixedTraits。
#include "killCmake.h"

#include<string>

using namespace std;

template<typename T>
struct SumFixedTraits;

template<>
struct SumFixedTraits<char>
{
	using sumT = int;
	static sumT initValue() {
		return 0;
	}
};

// 最求值策略技术时，为了求最小值，初始化需要很大
// 所以初始值可以为int最大值21亿
template<>
struct SumFixedTraits<int>
{
	using sumT = __int64;
	static sumT initValue() {
		return 2100000000;
	}
};

template<>
struct SumFixedTraits<double>
{
	using sumT = double;
	static sumT initValue() {
		return 0.0;
	}
};

template<typename T>
struct MinFixedTraits;

template<>
struct MinFixedTraits<int>
{
	// 求最小值，结果类型与元素类型相同即可
	// 为名字统一，都用sumT这个名字
	using sumT = int;

	static sumT initValue()
	{
		// 这里给整型最大值，相信任何一个数组元素都不会比这个值更大
		// 因此可以顺利找到数组元素中的最小值
		return INT_MAX;
	}
};

// 求和策略类以实现求和算法
struct SumPolicy
{
	// 静态成员函数模板
	template<typename sumT,typename T> // sumT是和值类型，T是数组元素类型
	static void algorithm(sumT& sum, const T& value) // 该策略类的核心算法
	{
		sum += value;
	}
};

template<typename T,typename U = SumFixedTraits<T>,typename V = SumPolicy>
auto funcsum(const T* begin, const T* end)
{
	typename U::sumT sum = U::initValue();

	for (;;)
	{
		// sum += (*begin); 此行被下面一行取代
		V::algorithm(sum, *begin);
		if (begin == end)
			break;
		++begin;
	}
	return sum;
}

struct MinPolicy
{
	template<typename minT,typename T>
	static void algorithm(minT& min, const T& value)
	{
		if (min > value)
			min = value;
	}
};

int main()
{
	int my_int_array1[] = { 10,15,20 };
	std::cout << funcsum<int, MinFixedTraits<int>, MinPolicy>(& my_int_array1[0], & my_int_array1[2]) << std::endl;

	return 0;
}

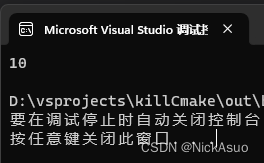
在这里插入图片描述
运行程序，新增的代码行结果为10，一切正常。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1294471.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

H3.3K27M弥漫性中线胶质瘤的反义寡核苷酸治疗

H3.3K27M弥漫性中线胶质瘤的反义寡核苷酸治疗

今天给同学们分享一篇实验文章“Antisense oligonucleotide therapy for H3.3K27M diffuse midline glioma”&#xff0c;这篇文章发表在Sci Transl Med期刊上&#xff0c;影响因子为17.1。 结果解读&#xff1a; CRISPR-Cas9消耗H3.3K27M恢复了H3K27三甲基化&#xff0c;并延…
阅读更多...
PHPstorm可选择版本的链接

PHPstorm可选择版本的链接

PHPstorm可选择版本的链接 链接&#xff1a;https://www.jetbrains.com/phpstorm/download/other.html
阅读更多...
class060 拓扑排序的扩展技巧【算法】

class060 拓扑排序的扩展技巧【算法】

class060 拓扑排序的扩展技巧【算法】 算法讲解060【必备】拓扑排序的扩展技巧 2023-12-7 22:23:02 code1 P4017 最大食物链计数 // 最大食物链计数 // a -> b&#xff0c;代表a在食物链中被b捕食 // 给定一个有向无环图&#xff0c;返回 // 这个图中从最初级动物到最顶…
阅读更多...
游戏被攻击怎么办

游戏被攻击怎么办

随着科技的进步和互联网的普及&#xff0c;游戏行业也正在经历前所未有的变革。玩家们不再满足于传统的线下游戏&#xff0c;而是转向了线上游戏。然而&#xff0c;随着游戏的线上化&#xff0c;游戏安全问题也日益凸显。游戏受到攻击是游戏开发者永远的痛点&#xff0c;谈“D“…
阅读更多...
laravel DB::connection 报错 Database connection [{$name}] not configured

laravel DB::connection 报错 Database connection [{$name}] not configured

DB::connection(mysql2);//不是连接数据库名
阅读更多...
Linus：我休假的时候也会带着电脑，否则会感觉很无聊

Linus：我休假的时候也会带着电脑，否则会感觉很无聊

目录 Linux 内核最新版本动态 关于成为内核维护者 代码好写&#xff0c;人际关系难处理 内核维护者老龄化 内核中 Rust 的使用 关于 AI 的看法 参考 12.5-12.6 日&#xff0c;Linux 基金会组织的开源峰会&#xff08;OSS&#xff0c;Open Source Summit&#xff09;在日…
阅读更多...
Enterprise Architect 12版本使用教程

Enterprise Architect 12版本使用教程

Enterprise Architect 12版本使用教程 1.下载安装Enterprise Architect 122.Enterprise Architect原始DDL模板配置及存在的问题1.DDL Column Definition原始模板&#xff08;没有default值&#xff1a;可忽略&#xff09;2.DDL Data Type原始模板&#xff08;timestamp等时间字…
阅读更多...
Diffusion 公式推导

Diffusion 公式推导

Diffusion&#xff1a;通过扩散和逆扩散过程生成图像的生成式模型 中已经对 diffusion 的原理进行了直观地梳理&#xff0c;本文对其中的数学推导进行讲解&#xff0c;还是基于 DDPM。 目录 一. 预备知识1. 重参数技巧2. 高斯分布的可加性3. 扩散递推式的由来 二. 扩散过程1. 背…
阅读更多...
企业计算机服务器中了360勒索病毒如何解密，勒索病毒解密数据恢复

企业计算机服务器中了360勒索病毒如何解密，勒索病毒解密数据恢复

网络技术的不断应用与发展&#xff0c;为企业的生产运营提供了极大便利&#xff0c;但随之而来的网络安全威胁也不断增加。近期&#xff0c;云天数据恢复中心接到很多企业的求助&#xff0c;企业的计算机服务器遭到了360后缀勒索病毒攻击&#xff0c;导致企业的所有数据被加密&…
阅读更多...
AtCoder ABC周赛2023 11/4 (Sat) E题题解

AtCoder ABC周赛2023 11/4 (Sat) E题题解

目录 原题截图&#xff1a; 原题翻译 题目大意&#xff1a; 主要思路&#xff1a; 代码&#xff1a; 原题截图&#xff1a; 原题翻译 题目大意&#xff1a; 给你一个数组&#xff0c;给你一个公式&#xff0c;让你选k个元素&#xff0c;用公式算出最终得分。 主要思路&am…
阅读更多...
云数据库与自建数据库有什么不同？

云数据库与自建数据库有什么不同？

「自购服务器搭建数据库服务」&#xff0c;涉及到云服务器和物理机服务器的选择。这两者之间存在一定的差别。首先&#xff0c;物理机服务器需要更多的部署及维护操作&#xff0c;而云服务器则通过虚拟化技术提供了更便捷的资源管理和弹性伸缩能力。 总体来说&#xff0c;部署在…
阅读更多...
移动云荣获OpenInfra社区“算力基础设施技术突破奖”

移动云荣获OpenInfra社区“算力基础设施技术突破奖”

近日&#xff0c;一年一度的 OpenInfra Days China在北京召开&#xff0c;大会汇聚了全球各大云厂商的技术专家&#xff0c;共同分享全球前沿基础设施技术的展望和实践经验。在本次大会上&#xff0c;移动云荣获OpenInfra社区颁发的“算力基础设施技术突破奖”&#xff0c;表明…
阅读更多...
销售技巧培训之如何提升顾问式销售技巧

销售技巧培训之如何提升顾问式销售技巧

销售技巧培训之如何提升顾问式销售技巧 在销售行业中&#xff0c;传统的“推销”模式往往注重产品的特点和优点&#xff0c;而忽视了客户的实际需求和感受。然而&#xff0c;随着消费者意识的提高和市场竞争的加剧&#xff0c;这种“产品导向”的销售方式已经不再适用。取而代…
阅读更多...
STM32的BKP与RTC简介

STM32的BKP与RTC简介

芯片的供电引脚 引脚表橙色的是芯片的供电引脚&#xff0c;其中VSS/VDD是芯片内部数字部分的供电&#xff0c;VSSA/VDDA是芯片内部模拟部分的供电&#xff0c;这4组以VDD开头的供电都是系统的主电源&#xff0c;正常使用时&#xff0c;全部都要接3.3V的电源上&#xff0c;VBAT是…
阅读更多...
实现跨VLAN通信、以及RIP路由协议的配置

实现跨VLAN通信、以及RIP路由协议的配置

一、如下图片&#xff1a; 1. 按照拓扑图所示&#xff0c;将8台计算机分别配置到相应的VLAN中。&#xff08;20分&#xff09; 2. 配置实现同一VLAN中的计算机可以通信。&#xff08;22分&#xff09; 3. 配置实现PC1,PC2,PC3,PC4可以互相通信&#xff0c;PC5,PC6,PC7,PC8可以互…
阅读更多...
JavaSE基础50题：19. 递归求斐波那契数列的第N项。

JavaSE基础50题：19. 递归求斐波那契数列的第N项。

概述 用递归求斐波那契数列的第N项。 斐波那契数列&#xff1a; 1 1 2 3 5 8 …… f(n) f(n-1) f(n-2) 代码 public class P19 {public static int fibnacio(int n) {if (n 1 || n 2) {return 1;}int tmp fibnacio(n-1) fibnacio(n-2);return tmp;}public static void…
阅读更多...
大数据技术4：Lambda和Kappa架构区别

大数据技术4：Lambda和Kappa架构区别

前言&#xff1a;在大数据处理领域&#xff0c;两种突出的数据架构已成为处理大量数据的流行选择&#xff1a;Lambda 架构和 Kappa 架构。这些架构为实时处理和批处理提供了强大的技术解决方案&#xff0c;使组织能够从其数据中获得有价值的见解。随着互联网时代来临&#xff0…
阅读更多...
No suitable driver found for jdbc:mysql://localhost:3306（2023/12/7更新）

No suitable driver found for jdbc:mysql://localhost:3306（2023/12/7更新）

有两种情况&#xff1a; 压根没安装下载了但没设为库或方法不对 大多数为第一种情况&#xff1a; 一. 下载jdbc 打开网址选择一个版本进行下载 https://nowjava.com/jar/version/mysql/mysql-connector-java.html 二.安装jdbc 在项目里建一个lib文件夹 在把之前下载的jar文…
阅读更多...
2017下半年软工(桥接模式)

2017下半年软工(桥接模式)

题目——桥接模式&#xff08;抽象调用实现部分&#xff09; package org.example.桥接模式;/*** 桥接模式的核心思想是将抽象部分与它的实现部分分离&#xff0c;使它们可以独立变化&#xff0c;就是说你在实现部分&#xff1a;WinImp、LinuxImp基础上还能加上RedHatImp&#…
阅读更多...
Java零基础——Elasticsearch篇

Java零基础——Elasticsearch篇

1.Elasticsearch简介 Elasticsearch是一个基于Lucene的一个开源的分布式、RESTful 风格的搜索和数据分析引擎。Elasticsearch是用Java语言开发的&#xff0c;并作为Apache许可条款下的开放源码发布&#xff0c;是一种流行的企业级搜索引擎。Elasticsearch用于云计算中&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023