圆和椭圆外投影

news2024/11/16 3:37:50

1 圆外一点在缩放到圆上

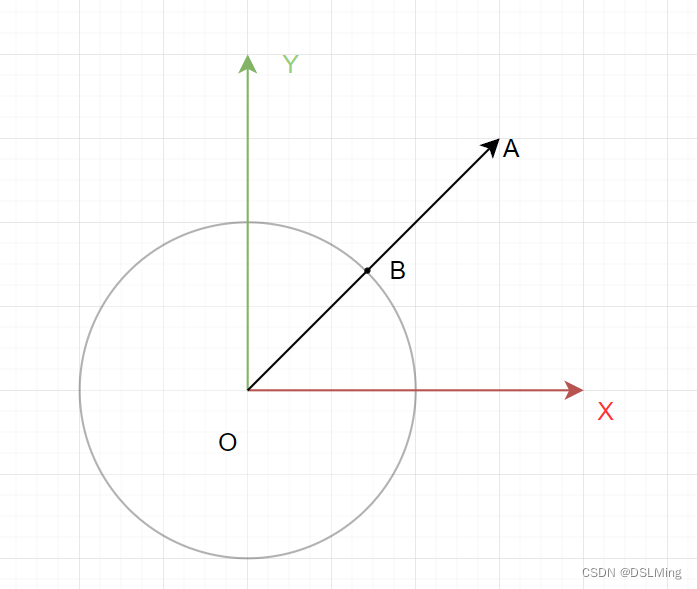
请添加图片描述

圆方程:
$x^2+y^2 = 2^2$

直线方程:
$y = k x$

圆外一点:
$A (3, 3)$

求点B.

方法1-解方程

圆外一点 $A (3, 3)$ ,那么:直线 $k = 1$ ,直线方程: $y = x$

方程联立:
$x^2 + x^2 = 4 \\$

$\sqrt{2} \\ y = \sqrt{2} \\$

方法2-向量

/**
 * 将圆外一点沿着圆心缩放到圆上,XOY平面
 * @param {number} circleRadius 圆半径
 * @param {Cesium.Cartesian3} point 园外点坐标
 */
function scaleToCircle(circleRadius=1, point=new Cesium.Cartesian3()) {
  const positionX = point.x;
  const positionY = point.y;

  // 将圆外一点带入圆方程
  const x2 = positionX * positionX;
  const y2 = positionY * positionY;

  // 圆外一点指向圆心方向向量的模长
  const squaredNorm = x2 + y2;
  const norm = Math.sqrt(squaredNorm);

  const ratio = circleRadius/norm;
  return Cesium.Cartesian3.multiplyByScalar(
    point,
    ratio,
    new Cesium.Cartesian3()
  );
}

const pointA = new Cesium.Cartesian3(3, 3, 0)
const pointB = scaleToCircle(2, cartesian1)
console.error(pointB);

2 椭圆外一点在椭圆上的投影

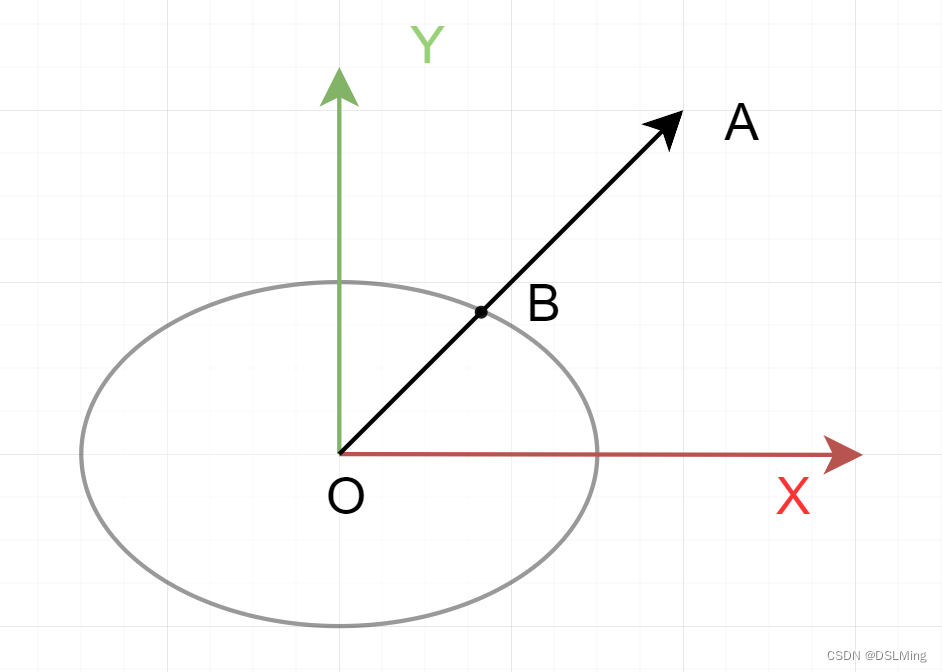
请添加图片描述

椭圆方程:
$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

直线方程:
$y = k x$

圆外一点:
$A (3, 3)$

求点B.

 /**
   *
   * @param {*} a
   * @param {*} b
   * @param {*} point
   * @returns
   */
  scaleToEllipsoid(a, b, point = new Cesium.Cartesian3()) {
    const positionX = point.x;
    const positionY = point.y;

    const x2 = positionX * positionX * (1 / (a * a));
    const y2 = positionY * positionY * (1 / (b * b));

    const squaredNorm = x2 + y2;
    const ratio = Math.sqrt(1/squaredNorm);

    return Cesium.Cartesian3.multiplyByScalar(
      point,
      ratio,
      new Cesium.Cartesian3()
    );
  }

证明:
椭圆外一点:
$\vec{n}$

椭圆方程:
$\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$

step1:
将椭圆外一点带入椭圆方程:
$\frac{c^2}{a^2}+\frac{d^2}{b^2} = S$

step2:
方向向量为:
$\frac{1}{\sqrt{S}} \vec{n} = ( \frac{c}{\sqrt{\frac{c^2}{a^2}+\frac{d^2}{b^2}}}, \frac{d}{\sqrt{\frac{c^2}{a^2}+\frac{d^2}{b^2}}}, )$

step3:
将方向向量带入椭圆方程:
$\begin{aligned} \frac{\frac{c}{\sqrt{\frac{c^2}{a^2}+\frac{d^2}{b^2}}}}{a^2} + \frac{\frac{d}{\sqrt{\frac{c^2}{a^2}+\frac{d^2}{b^2}}}}{b^2} &= ? \\ \frac{c^2}{a^2(\frac{c^2}{a^2}+\frac{d^2}{b^2})} + \frac{d^2}{b^2(\frac{d^2}{a^2}+\frac{d^2}{b^2})} &= ? \\ \frac{c^2}{c^2 + \frac{a^2d^2}{b^2}} + \frac{d^2}{\frac{b^2a^2}{a^2}d^2} &= ? \\ \frac{b^2c^2}{b^2c^2+a^2d^2} + \frac{a^2d^2}{b^2c^2+a^2d^2} &= 1 \end{aligned}$