今天开启单调栈的征程。
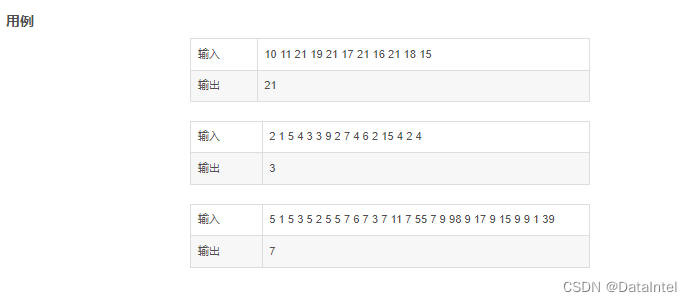
第一题:

简介:
本题有两种解法,第一种:暴力破解 两层for循环 时间复杂度为O(n^2) 超时了
第二种:单调栈解法也是今天的主角。
单调栈是什么?
- 单调递增栈:单调递增栈就是从栈顶到栈底是从小到大 作用场景:求解某一个在当前数左面或右面第一个大的数
- 单调递减栈:单调递减栈就是从栈顶到栈底数据是从大到小 作用场景:求解某一个在当前数左面或右面第一个小的数
单调栈的本质是空间换时间,因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素,优点是整个数组只需要遍历一次。
-
更直白来说,就是用一个栈来记录我们遍历过的元素,因为我们遍历数组的时候,我们不知道之前都遍历了哪些元素,以至于遍历一个元素找不到是不是之前遍历过一个更小的,所以我们需要用一个容器(这里用单调栈)来记录我们遍历过的元素。
在使用单调栈的时候首先要明确如下几点:
- 单调栈里存放的元素是什么? 单调栈里只需要存放元素的下标i就可以了,如果需要使用对应的元素,直接T[i]就可以获取。
- 单调栈里元素是递增呢? 还是递减呢?
本题思路:
本题我们使用单调栈,首先是由题意我们要求第一个大的数,所以我们使用单调递增栈。然后我建议大家用草稿纸来模拟一下整个单调栈的运行过程。
for(int i=1;i<temperatures.size();i++){
if(temperatures[i]>temperatures[st.top()]){
while(!st.empty() &&temperatures[i]>temperatures[st.top()]){
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}else if(temperatures[i] == temperatures[st.top()]){
st.push(i);
}else{
st.push(i);
}
}此代码为遍历过程,大家跟着走一遍就可明白单调栈工作流程。 或者可以去看代码随想路录算法视频跟着卡哥走一遍。
代码实现:
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> st;
vector<int> result(temperatures.size(),0);
st.push(0);
for(int i=1;i<temperatures.size();i++){
if(temperatures[i]>temperatures[st.top()]){
while(!st.empty() &&temperatures[i]>temperatures[st.top()]){
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}else if(temperatures[i] == temperatures[st.top()]){
st.push(i);
}else{
st.push(i);
}
}
return result;
}第二题:

简介:
本题相对于前一题,无太大差别,我们只需在本题中找出nums1中数值 对应 nums2 中的位置即可求出此题,其他代码与上题相同。
代码实现:
未优化版:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
stack<int> st;
vector<int> result(nums2.size(),-1);
vector<int> result2;
st.push(0);
for(int i=1;i<nums2.size();i++){
if( nums2[i]>nums2[st.top()]){
while(!st.empty() &&nums2[i]>nums2[st.top()]){
result[st.top()] = nums2[i];
st.pop();
}
st.push(i);
}else if(nums2[i] == nums2[st.top()]){
st.push(i);
}else{
st.push(i);
}
}
for(int i=0;i<nums2.size();i++){
cout<<result[i]<<" ";
}
for(int i=0;i<nums1.size();i++){
for(int j=0;j<nums2.size();j++){
if(nums1[i]==nums2[j]){
result2.push_back(result[j]);
break;
}
}
}
return result2;
}优化版:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
stack<int> st;
vector<int> result(nums1.size(), -1);
if (nums1.size() == 0) return result;
unordered_map<int, int> umap; // key:下标元素,value:下标
for (int i = 0; i < nums1.size(); i++) {
umap[nums1[i]] = i;
}
st.push(0);
for (int i = 1; i < nums2.size(); i++) {
if (nums2[i] < nums2[st.top()]) { // 情况一
st.push(i);
} else if (nums2[i] == nums2[st.top()]) { // 情况二
st.push(i);
} else { // 情况三
while (!st.empty() && nums2[i] > nums2[st.top()]) {
if (umap.count(nums2[st.top()]) > 0) { // 看map里是否存在这个元素
int index = umap[nums2[st.top()]]; // 根据map找到nums2[st.top()] 在 nums1中的下标
result[index] = nums2[i];
}
st.pop();
}
st.push(i);
}
}
return result;
}总结:
今天是单调栈的一天,我感觉只要明白单调栈的运行过程,就可以解决问题了。不算太难,继续加油!