目录

核心：

问题转化：

状态转化：（你得先读懂题，理解我们要干什么）

对应不同情况下的状态转化：（比如栈空就不能出栈，，）

AC代码：

---

题目：

P1044 [NOIP2003 普及组] 栈 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

核心：

这道题我当时根本不会做，甚至看半天题解看不懂，所以写一下懂后的理解

这道题递归的话一定要明确“状态”

当操作序列里没有数的时候，本次的输出序列就定死了

这个时候就可以递归结束，返回1了（即1种情况）

问题转化：

然后问题就转化成了，看有多少种“操作序列为空”情况。

（那是否可以趋近于操作序列为空呢？这个也是看题目的操作过程了）

状态转化：（你得先读懂题，理解我们要干什么）

我们设 i 为操作序列内数的数目 ， j 为栈内数的数目。

这个时候对应题目的两种操作：

1.入栈 i-1 , j+1

2.出栈 j-1

i 和 j 会有且仅有这两种变化。

对应不同情况下的状态转化：（比如栈空就不能出栈，，）

当i == 0时，结果就定死了，就返回0

当i != 0 , j != 0时，这个时候，可以入栈，也可以出栈   （有的题解说"入栈立马出"，这个相当于我们当前回合选择入栈，然后下一回合选择出栈）

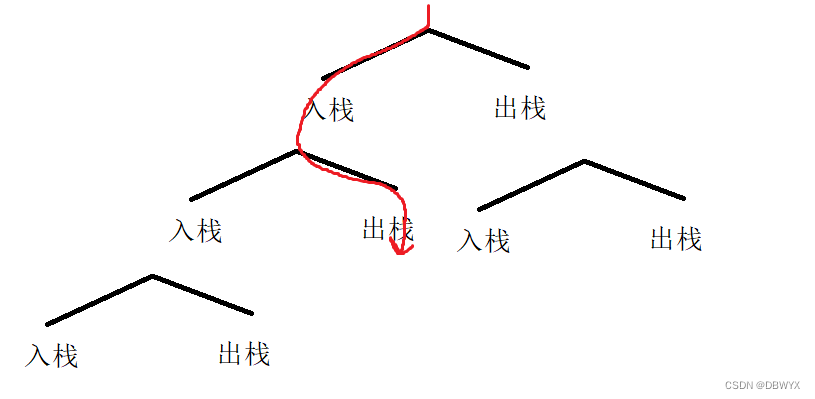
当j == 0的时候，你没法出栈啊，栈都空了，所以你只能入栈

AC代码：

long long dfs(int i,int j)
{
	if (i == 0)
		return 1;
	if (j == 0)
		return dfs(i - 1, j + 1);
	else
		return dfs(i - 1, j + 1) + dfs(i, j - 1);
}

int main()
{
	int n;
	cin >> n;
	cout << dfs(n,0);
	return 0;
}