Online Decision Based Visual Tracking via Reinforcement Learning

概述

本文2020年发布于NeurIPS(CCF-A)。视觉跟踪通常基于目标检测或者模板区配，但它们都只适用于特定的场景或对象。因为它们遵循不同的跟踪原则，直接将它们融合在一起是不明智的。

本文主要提出了一种新的视觉跟踪集成框架DTNet，它基于层次强化学习（HRL）的决策机制。该框架提供了一个基于规则的动态转换策略，其中探测和模板跟踪器必须相互竞争来决定使用谁来跟踪。此外，提出了一个新的检测追踪器，它可以避免错误建议的普遍问题（不需要建议目标的候选边界框，从而使识别过程灵活）。实验结果表明，DTNet达到了最先进的跟踪性能，并且实现了性能和效率之间的平衡。

方法

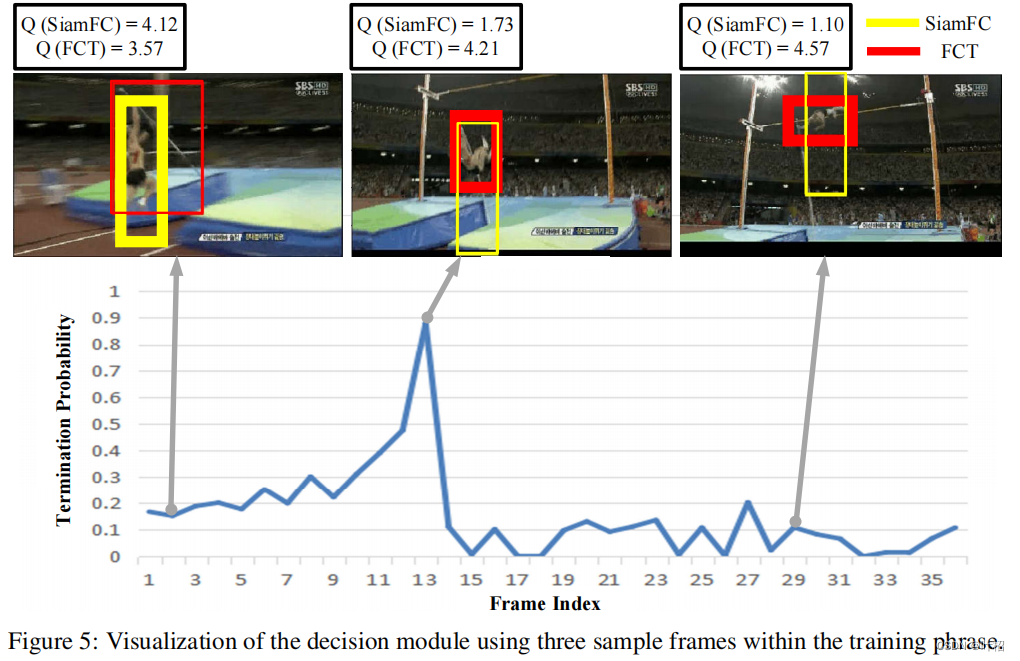
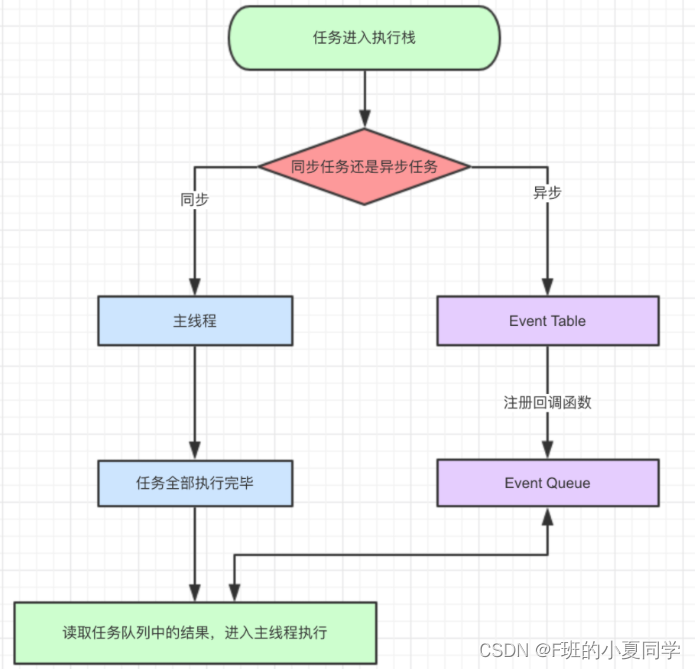
与融合方法不同，DTNet学习如何自动切换两种tracker适用于不同场景。该框架包含两个模块： decision module 和 tracker module。

• decision module

  • switch network：编码继承自前一帧$I_{t-1}$的 image patch ${\Phi }_t$ 和初始模板${\Phi }^{\ast }$，然后输出一个二进制信号选择tracker，该tracker从当前帧$I_t$中估计目标的位置。
  • termination network：估计tracker的输出，并决定是继续使用当前tracker还是终止该tracker（这使得 decision module 不会在两个tracker之间振荡）。如果决定终止，只能证明当前tracker性能不是很好而不能证明另一个tracker性能更好，此时使用switch network从两个tracker中选择一个。
    
    

  马尔可夫选择$w\in \Omega$由三部分组成：intra-option策略$\pi :S\times A\to [0,1]$，终止条件$\beta ：S^{+}\to [0,1]$，初始集合$I\subseteq S$。若采取$w$，根据${\pi }_w$选择动作，直到$w$根据${\beta }_w$终止。
  $Q_{\Omega }$表示switch network，可以被看做一个服从带网络权重$\theta$和终止网络${\beta }_{\Omega ,v}$的$\Omega$的函数。决定当前tracker是否被终止的终止概率是由${\beta }_{\Omega ,v}$根据选择$\Omega$和其网络权重$v$估计。将$Q_{\Omega }$定义如下，用HRL的方法评估option $w$的值：
  $$Q_{\Omega }(s,w;\theta )=r(s,w)+\lambda U(s^{{}^{\prime }},w)$$
  $r(s,w)$表示agent在采取$w$，选择一个特定tracker后收到的奖励。$U(s^{\prime },w)$是在与终止概率${\beta }_{w,v}$相关的新状态$s^{\prime }$执行$w$的值，通过结合switch和termination network输出的值来计算：
  $$U(s^{\prime },w)=(1-{\beta }_{w,\nu }(s^{\prime }))Q_{\Omega }(s^{\prime },w)+{\beta }_{w,\nu }(s^{\prime })V_{\Omega }(s^{\prime })$$
  ${\beta }_{w,\nu }(s^{\prime })$是在状态$s^{\prime }$的终止概率，$V_{\Omega }$是switch函数的最优解，它可以通过在option $w$上搜索switch函数$Q_{\Omega }$的最大值来得到：
  $$V_{\Omega }=\underset{w}{\max }(Q_{\Omega }(s^{\prime },w))$$
  如果当前的option表现为$w_{good}$，即${\beta }_{w,\nu }$趋近于0，$U(s^{\prime },w_{good})\approx Q_{\Omega }(s^{\prime },w_{good})$，反之，${\beta }_{w,\nu }$趋近于1，根据$V_{\Omega }=(Q_{\Omega }(s^{\prime },w_{good}))$，仍有$U(s^{\prime },w_{good})\approx Q_{\Omega }(s^{\prime },w_{good})$。$U(s,w)$是可微的，其关于termination network的权值$v$的梯度表示为：
  $$\frac{\partial U(s^{\prime },w)}{\partial v}=-\frac{\partial {\beta }_{w,v}(s^{\prime })}{\partial v}(Q_{\Omega }(s^{\prime },w)-V_{\Omega }(s^{\prime }))+(1-{\beta }_{w,v}(s^{\prime }))\frac{\partial U(s^{\prime \prime },w^{\prime })}{\partial v}$$
  switch network $Q_{\Omega }(s,w)$作为"Critic"评估option的值，并且为 termination network ${\beta }_{w,v}$提供更新梯度， termination network 本质上作为"Actor"，并且评估正在使用的tracker的性能以决定是否在当前帧终止它。switch network 的权重$\theta$通过贝尔曼公式学习。

• Tracker Module

  • Template tracker：使用 SiamFC作为Template tracker，标准的暹罗架构以一个包含一个范例图像$z$和一个候选图像$x$的图像对作为输入。

    • tips： Siamese network(https://zhuanlan.zhihu.com/p/35040994)

    $z$表示感兴趣的目标，而$x$通常更大，表示后续视频帧的搜索区域。$x$和$z$的特征由相同的$\tau$参数化的$CNN\phi$提取：
    $$f_{\tau }(z,x)={\phi }_{\tau }(z)\star {\phi }_{\tau }(x)+b$$
    $\star$表示卷积操作。该公式在$x$上对$z$进行了穷举搜索，目标是将响应映射$f$中的最大值区配到目标位置。

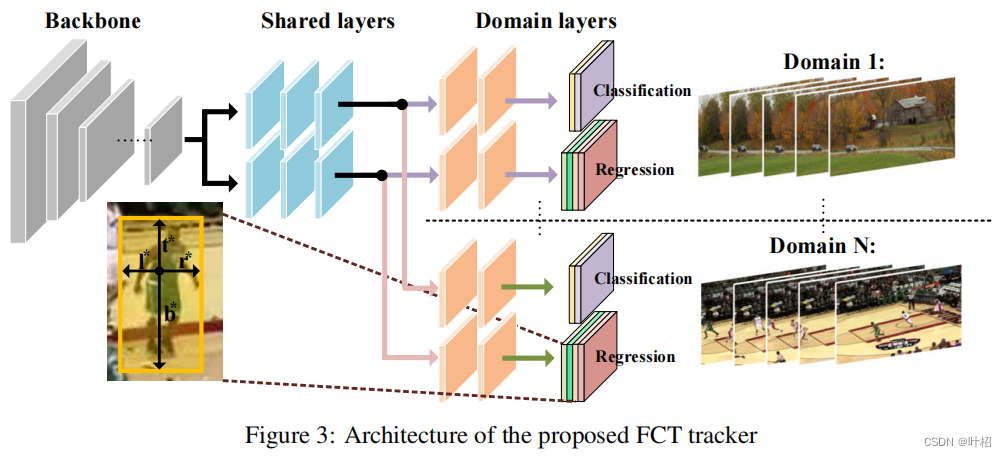
  • Detection tracker：为了构建一个基于目标检测的跟踪器，同时避免昂贵的提案生成过程，采用了一个全卷积tracker——FCT，包括一个分类分支和一个回归分支。分类分支预测目标位置，回归分支预测一个4D向量，表示从目标中心到其边界框的边缘的距离。
    给定主干CNN的特征映射$F\in R^{H\times W\times C}$和在前一层中应用的所有步长的和$s$，$F$中的每个位置$(x,y)$对应于图中的每个位置$(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys)$，直接预测F每个位置的类标签和回归距离。
    同一类object有可能被认为是一个序列的目标，但是另一个序列的背景，因此不能简单地使用传统分类器分配给目标‘1’或者‘0’。提出的分类branch，在每个域中，如果位置$(x,y)$落在groundtruth box，类标签$c^{\ast }$分配为‘1’，被视为正样本，否则类标签被分配为‘0’，视为负样本。
    回归分支输出一个4D矢量$r{e}^{\ast }=(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$，表示从目标的位置到边界框四个边界的距离（如图3）。跟踪器最终输出的分类得分映射$c$和回归值$re$，训练损失函数如下所示：
    $$L(c,r)=\frac{1}{N}\sum _{i=1}^N{L}_{cls}(c_i,c_i^{\ast })+\frac{\lambda }{N}[Where{c}^{\ast }>0]\sum _{i=1}^N{L}_{reg}(r{e}_i,r{e}_i^{\ast })$$
    N表示用来训练的视频帧的总数。

训练

给定$K$个训练序列，对第$j$个随机提取一条训练序列 I j = { I 1 j , I 2 j , . . . , I T j } I_j=\{I_{1j},I_{2j},...,I_{Tj}\} Ij​={I1j​,I2j​,...,ITj​}依次对应ground truth G j = { G 1 j , G 2 j , . . . , G T j } G_j=\{G_{1j},G_{2j},...,G_{Tj}\} Gj​={G1j​,G2j​,...,GTj​}，每对相邻的帧以一定概率跳过$n$帧$(0\le n\le 5)$。初始目标在第一帧的ground truth附近随机采样并作为模板，switch network有选择地评估模板编码的特征，观察结果继承自前一帧，并且选择一个tracker。switch过程中奖励如下：
$$r_t(s,w)=\{\begin{array}{l}{\eta }_L\cdot D_{IoU},IF(P_t>t{h}_{hi}and{P}_t^{\ast }<th{e}_{lo})\\ {\eta }_L\cdot D_{IoU},IF(P_t<t{h}_{hi}and{P}_t^{\ast }>th{e}_{lo})\\ {\eta }_M\cdot D_{IoU},IF(P_t>t{h}_{hi}and{P}_t^{\ast }>th{e}_{lo})\\ {\eta }_S\cdot D_{IoU},IF(P_t<t{h}_{hi}and{P}_t^{\ast }<th{e}_{lo})\end{array}$$
(如下图所示）$P_t$是所选tracker的预测边界框与ground truth $G_t$和$P_t^{\ast }$之间的$IoU$，$P_t^{\ast }$是未选tracker对应的$IoU$，$D_{IoU}$是它们之间的差值。有三种情况：（1）一个成功一个失败；（2）两个都成功；（3）两个都失败。三个较大的系数降序分配，在指导跟踪竞争的同时选择具有更高精度的agent，这些样本由未被选择的tracker依次采集以更新相应的网络。也就是，继续训练更糟的那个来保证两个tracker的竞争。新状态$s^{\prime }$由当前帧的预测更新，然后agent以${\beta }_{w,v}(s^{\prime })$的概率终止前一个option并且重新评估option的价值。
对switch module，‘Critic’ model $Q_{\Omega }(s,w)$可以通过贝尔曼公式学习，学习过程通过最小化如下损失实现：
$$L=\frac{1}{N}\sum _{i=1}^N(y_i-Q_{\Omega }(s_i,w_i;\theta ){)}^2$$
其中$y_i=r(s_i,w_i)+\gamma (1-{\beta }_{w_i,v}(s_i^{\prime })Q_{\Omega }(s_i^{\prime },w_i))+{\beta }_{w_i,v}(s_i^{\prime })V_{\Omega }(s_i^{\prime })$。’Actor‘ module ${\beta }_{w,v}$更新如下：
$$v=v-{\alpha }_v\frac{\partial {\beta }_{w,v}(s^{\prime })}{\partial v}(Q_{\Omega }(s^{\prime },w)-V_{\Omega }(s^{\prime }))$$