KD-Tree

news2025/1/20 16:16:30

游戏中常对物体进行空间划分，对于均匀分布的划分一般用四叉树(八叉树)，动态不均匀的分布可以采用kd-tree

构建kd-tree

构建思路：

  • 1.对节点进行各维度的方差分析，选取方差最大(即离散程度最高)的维度进行排序。取中值节点作为分割点。并将其放入构建树的节点中
  • 2.被排序的节点按不同维度分割后，划分为力左空间(划分维度下小于分割节点的值)与右空间(划分维度下大于分割节点的值)。对两个空间重复步骤1，并且两个空间的分割点分别作为上一个分割点的左右子树加入构建树中。
    (设置维度除了分析方差，有时会选择所有维度循环设置)

树的节点的结构

struct TreeNode {
    int id; //节点唯一id
    Vec2 pos;
    int split; //分割维度
    struct TreeNode* left;
    struct TreeNode* right;
    struct TreeNode* parent;
};

获取分割维度

//计算所有节点各维度的方差，确定分割维度
int KDTreeScene::chooseSplit(vector<Vec2> posData) {
    float xEx1 = 0;
    float xEx2 = 0;
    float xDx = 0;
    float size = posData.size();
    for (auto v : posData) {
        xEx1 += 1.0 / size * v.x * v.x;
        xEx2 += 1.0 / size * v.x;
    }
    xDx = xEx1 - xEx2 * xEx2;
    float yEx1 = 0;
    float yEx2 = 0;
    float yDx = 0;
    for (auto v : posData) {
        yEx1 += 1.0 / size * v.y * v.y;
        yEx2 += 1.0 / size * v.y;
    }
    yDx = yEx1 - yEx2 * yEx2;
    return xDx >= yDx ? 0 : 1;
}

构建树

//rect是画分割线的辅助参数，实际应用可无视
TreeNode* KDTreeScene::buildKdTree(vector<Vec2> posData, Rect rect, int splitIdx) {
    if (posData.size() == 0) return nullptr;
    int split = chooseSplit(posData); //根据方差设置维度
    //split = splitIdx; //循环设置维度
    if (posData.size() == 1) {
    	//空间只剩一个节点，无需再划分
        TreeNode* TNode = new TreeNode();
        TNode->id = _id;
        _id++;
        TNode->pos = posData[0];
        TNode->left = nullptr;
        TNode->right = nullptr;
        TNode->split = split;
        //根据维度画分割线
        drawClipLine(rect, split, posData[0]);
        return TNode;
    }
    int mid = posData.size() / 2;
    vector<Vec2> leftPosData;
    vector<Vec2> rightPosData;

	//根据设置的维度进行排序
    if (split == 0) sort(posData.begin(), posData.end(), cmpX); //垂直x轴分割，则根据x值排序
    else sort(posData.begin(), posData.end(), cmpY); //垂直y轴分割，则根据y值排序

	//获取中值作为分割点
    Vec2 midPos = posData[mid];
    //小于中值的放入左空间
    for (int i = 0; i < mid; i++) {
        leftPosData.push_back(posData[i]);
    }
    //大于中值的放入右空间
    for (int j = mid + 1; j < posData.size(); j++) {
        rightPosData.push_back(posData[j]);
    }
    //创建树的节点
    TreeNode* TNode = new TreeNode();
    TNode->id = _id;
    _id++;
    TNode->pos = midPos;
    drawClipLine(rect, split, midPos);
    // ---------------------
    //用来画分割线的辅助参数，实际应用可无视
    Rect r1, r2;
    if (split == 0) {
        r1 = Rect(rect.getMinX(), rect.getMinY(), midPos.x - rect.getMinX(), rect.getMaxY() - rect.getMinY());
        r2 = Rect(midPos.x, rect.getMinY(), rect.getMaxX() - midPos.x, rect.getMaxY() - rect.getMinY());
    }
    else {
        r1 = Rect(rect.getMinX(), rect.getMinY(), rect.getMaxX() - rect.getMinX(), midPos.y - rect.getMinY());
        r2 = Rect(rect.getMinX(), midPos.y, rect.getMaxX() - rect.getMinX(), rect.getMaxY() - midPos.y);
    }
    // ---------------------
    //splitIdx++;  //循环遍历设置维度的方法
    //对左空间进行kd树的构建步骤，并把顶点作为当前节点的左子树
    TNode->left = buildKdTree(leftPosData, r1, splitIdx % 2);
    if (TNode->left != nullptr) TNode->left->parent = TNode;
    //对右空间进行kd树的构建步骤，并把顶点作为当前节点的右子树
    TNode->right = buildKdTree(rightPosData, r2, splitIdx % 2);
    if (TNode->right != nullptr) TNode->right->parent = TNode;
    TNode->split = split;
    //返回的节点为当前空间构造的kd树的顶点
    return TNode;
}

效果演示

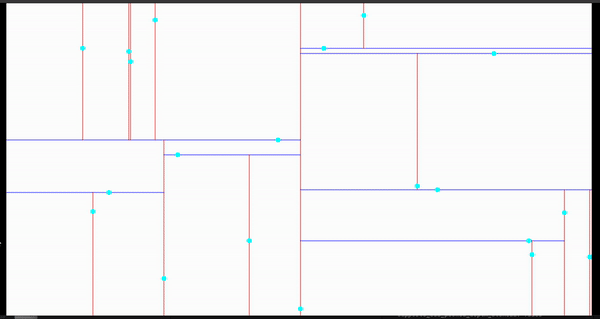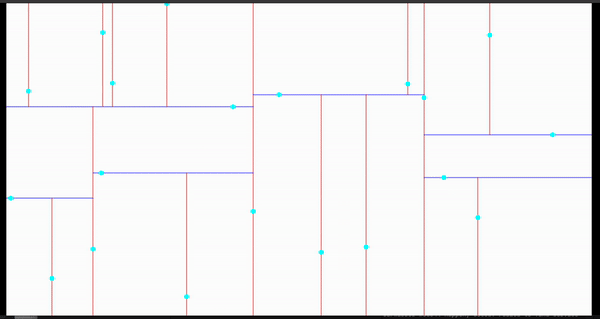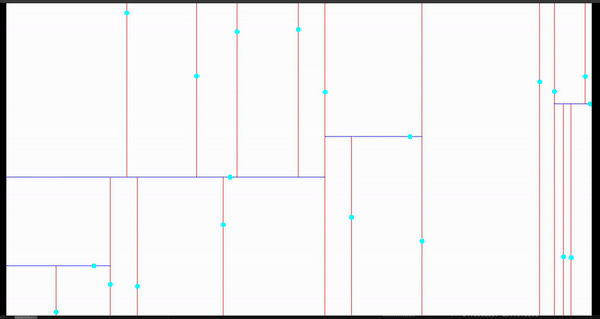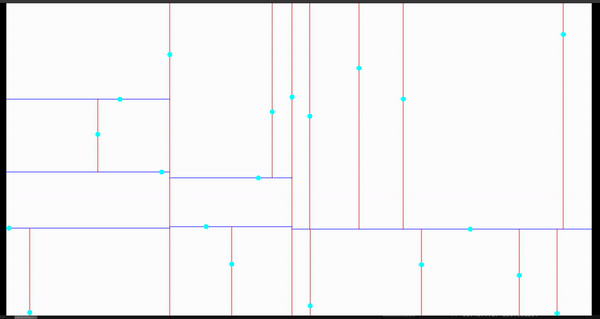
请添加图片描述

近邻搜寻

搜寻思路

维护一个最近邻居的优先级队列，以及一个记录访问过节点的表

  • 1.从根节点开始，将目标点递归往下查询。与插入思路一样，当前维度小于当前节点值的查询左子树，大于当前节点值的查询右子树。直到移动到叶子节点，将叶子节点进行访问。
  • 2.访问叶子节点。如果最近邻居优先级队列里的值小于所需邻居值，或者该叶子节点到目标点的距离小于队列中最远的邻居节点到目标点的距离。则将该叶子节点更新到最近邻居的队列，记录访问过的当前节点
  • 3.从叶子节点往上查询，(获取该叶子节点的父节点或着解开递归等方式)。对父节点进行访问处理(步骤2)。如果父节点已经访问过，则继续往上(重复步骤3)
  • 4.对该父节点对应维度的分割边进行距离判定：
    1.如果最近邻居优先级队列里的值小于所需邻居值或者目标点到分割边的垂直距离小于队列中最远的邻居节点到目标点的距离，则对该父节点的另一半空间进行从步骤1开始往下的查询
    2.否则，直接忽略该父节点的另一半空间，继续往上查询(回到步骤3)

往上的查询直到树的顶点即停止

void KDTreeScene::searchNearestPoint(Vec2 pos, TreeNode* tNode) {
    while (!_nearestQueue.empty()) {
        _nearestQueue.pop();
    }
    _searchDrawNode->clear();
    _exploredMap.clear();
    _searchDrawNode->drawDot(pos, 5, Color4F(0, 1, 0, 1));

//-----------------
	//进入搜寻
    TreeNode* leaf = searchLeafNode(pos, _kdTree);
    backCheck(pos, leaf);
//-----------------

//下面是画出搜寻结果
    while (!_nearestQueue.empty()) {
        _searchDrawNode->drawDot(_nearestQueue.top().second->pos, 5, Color4F(0, 0, 0, 1));
        if (_model) {
            delete _nearestQueue.top().second;
        }
        _nearestQueue.pop();
    }
}

访问对应节点

上述步骤2

bool KDTreeScene::checkInsertQueue(Vec2 pos, TreeNode* tNode) {
	//记录以访问过的节点
    _exploredMap[tNode->id] = true;
    //_searchNode是需要获取的最近邻居节点数
    //近邻居优先级队列里的值小于所需邻居值，则直接插入队列
    if (_nearestQueue.size() < _searchNode) {
        _nearestQueue.emplace(pos.getDistance(tNode->pos), tNode);
        return true;
    }
    else {
        auto data = _nearestQueue.top();
        float dist = pos.getDistance(tNode->pos);
        //该叶子节点到目标点的距离小于队列中最远的邻居节点到目标点的距离，则更新队列
        if (dist < data.first) {
            _nearestQueue.pop();
            _nearestQueue.emplace(dist, tNode);
            return true;
        }
    }
    return false;
}

递归查询到叶节点

上述步骤1

TreeNode* KDTreeScene::searchLeafNode(Vec2 pos, TreeNode* tNode) {
    if (tNode->split == 0) {
        if (pos.x < tNode->pos.x) {
            if (tNode->left == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->left);
        }
        else {
            if (tNode->right == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->right);
        }
    }
    else {
        if (pos.y < tNode->pos.y) {
            if (tNode->left == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->left);
        }
        else {
            if (tNode->right == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->right);
        }
    }
}

往上查询

上述步骤3和4

void KDTreeScene::backCheck(Vec2 pos, TreeNode* tNode) {
	//到顶点停止
    if (tNode->parent == nullptr) {
        return;
    }
    else {
    	//步骤3
        tNode = tNode->parent;
        //已经访问过的节点直接跳过，往上查询
        if (!_exploredMap[tNode->id]) {
        	//访问父节点
            checkInsertQueue(pos, tNode);
            if (tNode->split == 0) {
            	//步骤4
                if (_nearestQueue.size() < _searchNode || abs(pos.x - tNode->pos.x) < _nearestQueue.top().first) {
                	//步骤4 情况1
                	//----------------------
                    if (pos.x < tNode->pos.x) {
                        if(tNode->right) tNode = searchLeafNode(pos, tNode->right);
                    }
                    else {
                        if (tNode->left) tNode = searchLeafNode(pos, tNode->left);
                    }
                    //----------------------
                }
            }
            else {
                if (_nearestQueue.size() < _searchNode || abs(pos.y - tNode->pos.y) < _nearestQueue.top().first) {
                    if (pos.y < tNode->pos.y) {
                        if (tNode->right) tNode = searchLeafNode(pos, tNode->right);
                    }
                    else {
                        if (tNode->left) tNode = searchLeafNode(pos, tNode->left);
                    }
                }
            }
        }
        backCheck(pos, tNode);
    }
}

效果演示

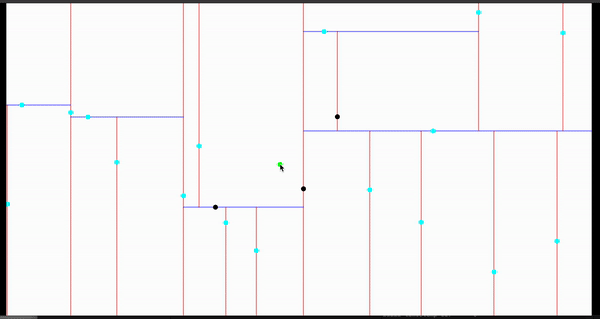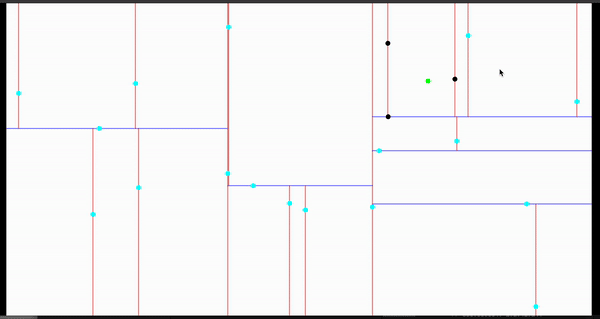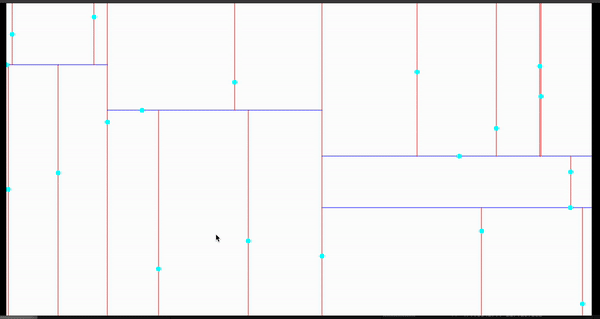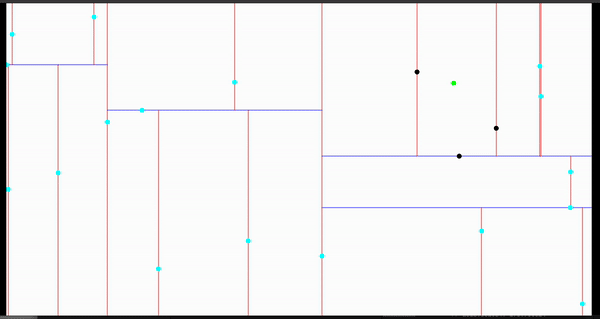
请添加图片描述

完整效果

以下是对2000个物体查询最近的6个邻居的效果：
请添加图片描述

对比了下对所有物体进行遍历找寻最近值的方式
搜寻3个最近物体时，在1000个时差不多开始出现1ms的延迟，在5000个3到4ms内的延迟，在10000个时7ms延迟, 在100000时70ms延迟， 就是成正比的延迟，
而kd树的查询到10000000仍是0，因为是类似二叉树的log的复杂度
主要耗时在构造树，1000个物体差不多5ms，5000个物体30ms，10000个物体50ms，100000个物体550ms，1000000个物体6400ms，5000000个物体37000ms，10000000个物体76000ms，差不多也是正比
不同机器效率不同，但是趋势一样

代码

KDTreeScene.h

#ifndef __KDTREE_SCENE_H__
#define __KDTREE_SCENE_H__

#include "cocos2d.h"
USING_NS_CC;
using namespace std;

struct TreeNode {
    int id;
    Vec2 pos;
    int split;
    struct TreeNode* left;
    struct TreeNode* right;
    struct TreeNode* parent;
};

struct cmp {
    bool operator()(pair<float, TreeNode*>& a, pair<float, TreeNode*>& b) {
        return a.first < b.first;
    }
};

class KDTreeScene : public Scene
{
public:
    static Scene* createScene();

    virtual bool init();

    virtual bool onTouchBegan(Touch* touch, Event* unused_event);

    TreeNode* buildKdTree(vector<Vec2> posData, Rect rect, int splitIdx);
    int chooseSplit(vector<Vec2> posData);
    void drawClipLine(Rect rect, int split, Vec2 pos);
    void searchNearestPoint(Vec2 pos, TreeNode* tNode);
    TreeNode* searchLeafNode(Vec2 pos, TreeNode* tNode);
    void backCheck(Vec2 pos, TreeNode* tNode);
    bool checkInsertQueue(Vec2 pos, TreeNode* tNode);

    // implement the "static create()" method manually
    CREATE_FUNC(KDTreeScene);

    void update(float dt);

protected:
    EventListenerTouchOneByOne* _touchListener;
    Vec2 _touchBeganPosition;
    DrawNode* _mapDrawNode;
    DrawNode* _clipDrawNode;

    vector<Vec2> _posData;
    TreeNode* _kdTree;
    bool _isDrawSplitLine = false;

    DrawNode* _searchDrawNode;
    int _searchNode = 6;
    priority_queue<pair<float, TreeNode*>,  vector<pair<float, TreeNode*>>, cmp> _nearestQueue;
    int _id;
    unordered_map<int, bool> _exploredMap;

    bool _model = false;
};

#endif

KDTreeScene.cpp

#include "KDTreeScene.h"
#include <chrono>
using namespace std::chrono;

Scene* KDTreeScene::createScene()
{
    return KDTreeScene::create();
}

static void problemLoading(const char* filename)
{
    printf("Error while loading: %s\n", filename);
    printf("Depending on how you compiled you might have to add 'Resources/' in front of filenames in KDTreeScene.cpp\n");
}

// on "init" you need to initialize your instance
bool KDTreeScene::init()
{
    //
    // 1. super init first
    if (!Scene::init())
    {
        return false;
    }
    auto visibleSize = Director::getInstance()->getVisibleSize();
    Vec2 origin = Director::getInstance()->getVisibleOrigin();

    auto layer = LayerColor::create(Color4B(255, 255, 255, 255));
layer:setContentSize(visibleSize);
    this->addChild(layer);

    _clipDrawNode = DrawNode::create();
    this->addChild(_clipDrawNode);
    _mapDrawNode = DrawNode::create();
    this->addChild(_mapDrawNode);
    _searchDrawNode = DrawNode::create();
    this->addChild(_searchDrawNode);

    auto drawNode = DrawNode::create();
    this->addChild(drawNode);
    auto vecData = vector<Vec2>{ Vec2::ZERO, Vec2(100,0), Vec2(100,640), Vec2(0,640) };
    Vec2* ptr = reinterpret_cast<Vec2*>(vecData.data());
    drawNode->drawPolygon(ptr, vecData.size(), Color4F(0, 0, 0, 1), 0, Color4F(0, 0, 0, 0));
    auto vecData1 = vector<Vec2>{ Vec2(1300,0), Vec2(1400,0), Vec2(1400,640), Vec2(1300,640) };
    Vec2* ptr1 = reinterpret_cast<Vec2*>(vecData1.data());
    drawNode->drawPolygon(ptr1, vecData1.size(), Color4F(0, 0, 0, 1), 0, Color4F(0, 0, 0, 0));

    _touchListener = EventListenerTouchOneByOne::create();
    _touchListener->setSwallowTouches(true);
    _touchListener->onTouchBegan = CC_CALLBACK_2(KDTreeScene::onTouchBegan, this);
    this->getEventDispatcher()->addEventListenerWithSceneGraphPriority(_touchListener, layer);

    this->scheduleUpdate();
    return true;
}

bool KDTreeScene::onTouchBegan(Touch* touch, Event* event)
{
    _touchBeganPosition = touch->getLocation();
    CCLOG("xxxxxxxxx==========>> %f? %f", _touchBeganPosition.x, _touchBeganPosition.y);
    if (_touchBeganPosition.x < 100) {
        _posData.clear();
        _mapDrawNode->clear();
        _clipDrawNode->clear();
        _searchDrawNode->clear();
        _id = 1;
        for (int i = 0; i < 5000000; i++) {
            float x = RandomHelper::random_real<float>(100, 1300);
            float y = RandomHelper::random_real<float>(0, 640);
            _posData.push_back(Vec2(x, y));
//            _mapDrawNode->drawDot(Vec2(x, y), 3, Color4F(0, 1, 1, 1));
        }
        auto last = std::chrono::system_clock::now();
        auto timestamp = std::chrono::time_point_cast<std::chrono::milliseconds>(last).time_since_epoch().count();
        _kdTree = buildKdTree(_posData, Rect(0, 0, 1400, 640), 0);
        _kdTree->parent = nullptr;
        auto now = std::chrono::system_clock::now();
        auto timestamp1 = std::chrono::time_point_cast<std::chrono::milliseconds>(now).time_since_epoch().count();
        CCLOG("build timestamp dif      %d", timestamp1 - timestamp);
    }
    else if (_touchBeganPosition.x > 1300) {
        _model = !_model;
    }
    else {
        if (_posData.empty()) {
            _id = 1;
            for (int i = 0; i < 2000; i++) {
                float x = RandomHelper::random_real<float>(100, 1300);
                float y = RandomHelper::random_real<float>(0, 640);
                _posData.push_back(Vec2(x, y));
//                _mapDrawNode->drawDot(Vec2(x, y), 3, Color4F(0, 1, 1, 1));
            }
            auto last = std::chrono::system_clock::now();
            auto timestamp = std::chrono::time_point_cast<std::chrono::milliseconds>(last).time_since_epoch().count();
            _kdTree = buildKdTree(_posData, Rect(0, 0, 1400, 640), 0);
            _kdTree->parent = nullptr;
            auto now = std::chrono::system_clock::now();
            auto timestamp1 = std::chrono::time_point_cast<std::chrono::milliseconds>(now).time_since_epoch().count();
            CCLOG("build timestamp dif       %d", timestamp1 - timestamp);
            return true;
        }
        searchNearestPoint(_touchBeganPosition, _kdTree);
    }
    return true;
}

void KDTreeScene::update(float dt) {

}

bool cmpX(Vec2 a, Vec2 b) {
    return a.x < b.x;
}

bool cmpY(Vec2 a, Vec2 b) {
    return a.y < b.y;
}

int KDTreeScene::chooseSplit(vector<Vec2> posData) {
    float xEx1 = 0;
    float xEx2 = 0;
    float xDx = 0;
    float size = posData.size();
    for (auto v : posData) {
        xEx1 += 1.0 / size * v.x * v.x;
        xEx2 += 1.0 / size * v.x;
    }
    xDx = xEx1 - xEx2 * xEx2;
    float yEx1 = 0;
    float yEx2 = 0;
    float yDx = 0;
    for (auto v : posData) {
        yEx1 += 1.0 / size * v.y * v.y;
        yEx2 += 1.0 / size * v.y;
    }
    yDx = yEx1 - yEx2 * yEx2;
    return xDx >= yDx ? 0 : 1;
}

TreeNode* KDTreeScene::buildKdTree(vector<Vec2> posData, Rect rect, int splitIdx) {
    if (posData.size() == 0) return nullptr;
    int split = chooseSplit(posData);
    //split = splitIdx;
    if (posData.size() == 1) {
        TreeNode* TNode = new TreeNode();
        TNode->id = _id;
        _id++;
        TNode->pos = posData[0];
        TNode->left = nullptr;
        TNode->right = nullptr;
        TNode->split = split;
        drawClipLine(rect, split, posData[0]);
        return TNode;
    }
    int mid = posData.size() / 2;
    vector<Vec2> leftPosData;
    vector<Vec2> rightPosData;

    if (split == 0) sort(posData.begin(), posData.end(), cmpX);
    else sort(posData.begin(), posData.end(), cmpY);

    Vec2 midPos = posData[mid];
    for (int i = 0; i < mid; i++) {
        leftPosData.push_back(posData[i]);
    }
    for (int j = mid + 1; j < posData.size(); j++) {
        rightPosData.push_back(posData[j]);
    }
    TreeNode* TNode = new TreeNode();
    TNode->id = _id;
    _id++;
    TNode->pos = midPos;
    drawClipLine(rect, split, midPos);
    Rect r1, r2;
    if (split == 0) {
        r1 = Rect(rect.getMinX(), rect.getMinY(), midPos.x - rect.getMinX(), rect.getMaxY() - rect.getMinY());
        r2 = Rect(midPos.x, rect.getMinY(), rect.getMaxX() - midPos.x, rect.getMaxY() - rect.getMinY());
    }
    else {
        r1 = Rect(rect.getMinX(), rect.getMinY(), rect.getMaxX() - rect.getMinX(), midPos.y - rect.getMinY());
        r2 = Rect(rect.getMinX(), midPos.y, rect.getMaxX() - rect.getMinX(), rect.getMaxY() - midPos.y);
    }
    splitIdx++;
    TNode->left = buildKdTree(leftPosData, r1, splitIdx % 2);
    if (TNode->left != nullptr) TNode->left->parent = TNode;
    TNode->right = buildKdTree(rightPosData, r2, splitIdx % 2);
    if (TNode->right != nullptr) TNode->right->parent = TNode;
    TNode->split = split;
    return TNode;
}

void KDTreeScene::drawClipLine(Rect rect, int split, Vec2 pos) {
//    if (split == 0) {
//        _clipDrawNode->drawSegment(Vec2(pos.x, rect.getMinY()), Vec2(pos.x, rect.getMaxY()), 1, Color4F(1, 0, 0, 0.5));
//    }
//    else {
//        _clipDrawNode->drawSegment(Vec2(rect.getMinX(), pos.y), Vec2(rect.getMaxX(), pos.y), 1, Color4F(0, 0, 1, 0.5));
//    }
}

void KDTreeScene::searchNearestPoint(Vec2 pos, TreeNode* tNode) {
    while (!_nearestQueue.empty()) {
        _nearestQueue.pop();
    }
    _searchDrawNode->clear();
    _exploredMap.clear();
    _searchDrawNode->drawDot(pos, 3, Color4F(1, 0, 0, 1));
    auto last = std::chrono::system_clock::now();
    auto timestamp = std::chrono::time_point_cast<std::chrono::milliseconds>(last).time_since_epoch().count();
    if (_model) {
        for (auto p : _posData) {
            TreeNode* t = new TreeNode();
            t->id = _id;
            _id++;
            t->pos = p;
            checkInsertQueue(pos, t);
        }
    }
    else {
        TreeNode* leaf = searchLeafNode(pos, _kdTree);
        backCheck(pos, leaf);
    }
    auto now = std::chrono::system_clock::now();
    auto timestamp1 = std::chrono::time_point_cast<std::chrono::milliseconds>(now).time_since_epoch().count();
    CCLOG("search timestamp dif       %d", timestamp1 - timestamp);
    while (!_nearestQueue.empty()) {
        _searchDrawNode->drawDot(_nearestQueue.top().second->pos, 3, Color4F(0, 0, 0, 1));
        if (_model) {
            delete _nearestQueue.top().second;
        }
        _nearestQueue.pop();
    }
}

bool KDTreeScene::checkInsertQueue(Vec2 pos, TreeNode* tNode) {
    _exploredMap[tNode->id] = true;
    if (_nearestQueue.size() < _searchNode) {
        _nearestQueue.emplace(pos.getDistance(tNode->pos), tNode);
        return true;
    }
    else {
        auto data = _nearestQueue.top();
        float dist = pos.getDistance(tNode->pos);
        if (dist < data.first) {
            _nearestQueue.pop();
            _nearestQueue.emplace(dist, tNode);
            return true;
        }
    }
    return false;
}

TreeNode* KDTreeScene::searchLeafNode(Vec2 pos, TreeNode* tNode) {
    if (tNode->split == 0) {
        if (pos.x < tNode->pos.x) {
            if (tNode->left == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->left);
        }
        else {
            if (tNode->right == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->right);
        }
    }
    else {
        if (pos.y < tNode->pos.y) {
            if (tNode->left == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->left);
        }
        else {
            if (tNode->right == nullptr) {
                checkInsertQueue(pos, tNode);
                return tNode;
            }
            else return searchLeafNode(pos, tNode->right);
        }
    }
}

void KDTreeScene::backCheck(Vec2 pos, TreeNode* tNode) {
    if (tNode->parent == nullptr) {
        return;
    }
    else {
        tNode = tNode->parent;
        if (!_exploredMap[tNode->id]) {
            checkInsertQueue(pos, tNode);
            if (tNode->split == 0) {
                if (_nearestQueue.size() < _searchNode || abs(pos.x - tNode->pos.x) < _nearestQueue.top().first) {
                    if (pos.x < tNode->pos.x) {
                        if(tNode->right) tNode = searchLeafNode(pos, tNode->right);
                    }
                    else {
                        if (tNode->left) tNode = searchLeafNode(pos, tNode->left);
                    }
                }
            }
            else {
                if (_nearestQueue.size() < _searchNode || abs(pos.y - tNode->pos.y) < _nearestQueue.top().first) {
                    if (pos.y < tNode->pos.y) {
                        if (tNode->right) tNode = searchLeafNode(pos, tNode->right);
                    }
                    else {
                        if (tNode->left) tNode = searchLeafNode(pos, tNode->left);
                    }
                }
            }
        }
        backCheck(pos, tNode);
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1290515.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

ThreadX开源助力Microsoft扩大应用范围：对比亚马逊AWS的策略差异

ThreadX开源助力Microsoft扩大应用范围：对比亚马逊AWS的策略差异

全球超过120亿台设备正在运行ThreadX&#xff0c;这是一款专为资源受限环境设计的实时操作系统。该操作系统在微控制器和小型处理器上表现出色&#xff0c;以极高的可靠性和精确的时间控制处理任务而闻名。 ThreadX曾是英特尔芯片管理引擎的引擎&#xff0c;并且是控制Raspber…
阅读更多...
运行第一个php及html程序

运行第一个php及html程序

运行第一个php程序 打开vscode&#xff0c;打开文件夹&#xff0c;找到wampserver的安装目录中的www文件夹新建文件。 html文件直接复制路径到浏览器即可运行 php文件复制路径到浏览器后更改www及之前的路径为localhost
阅读更多...
Linux系统调试课：I2C tools调试工具

Linux系统调试课：I2C tools调试工具

文章目录 一、如何使用I2C tools测试I2C外设1、I2C tools概述： 2、下载I2C tools源码：3、编译I2C tools源码： 4、i2cdetect 5、i2cget 6、i2cdump
阅读更多...
STM32单片机项目实例：基于TouchGFX的智能手表设计（3）嵌入式程序任务调度的设计

STM32单片机项目实例：基于TouchGFX的智能手表设计（3）嵌入式程序任务调度的设计

STM32单片机项目实例&#xff1a;基于TouchGFX的智能手表设计&#xff08;3&#xff09;嵌入式程序任务调度的设计 目录 一、嵌入式程序设计 1.1轮询 1.2 前后台&#xff08;中断轮询&#xff09; 1.3 事件驱动与消息 1.3.1 事件驱动的概念 1.4 定时器触发事件驱动型的任…
阅读更多...
7. 从零用Rust编写正反向代理, HTTP及TCP内网穿透原理及运行篇

7. 从零用Rust编写正反向代理, HTTP及TCP内网穿透原理及运行篇

wmproxy wmproxy是由Rust编写&#xff0c;已实现http/https代理&#xff0c;socks5代理&#xff0c; 反向代理&#xff0c;静态文件服务器&#xff0c;内网穿透&#xff0c;配置热更新等&#xff0c; 后续将实现websocket代理等&#xff0c;同时会将实现过程分享出来&#xff…
阅读更多...
分布式光伏电站监控运维系统的简单介绍-安科瑞黄安南

分布式光伏电站监控运维系统的简单介绍-安科瑞黄安南

摘要&#xff1a;设计了一套更高性价比&#xff0c;且容易操作的电站监控系统。该系统融合了互联网和物联网&#xff0c;并为光伏电数据的传输构建了相应的通道&#xff0c;可支持云存储等功能&#xff0c;同时也为用户提供了多元化的查询功能。 关键词&#xff1a;分布式太阳能…
阅读更多...
P6 Linux 系统中的文件类型

P6 Linux 系统中的文件类型

目录 前言 ​编辑 01 linux系统查看文件类型 02 普通文件 - 03 目录文件 d 04 字符设备文件 c 和块设备文件 b 05 符号链接文件 l 06 管道文件 p 07 套接字文件 s 总结 前言 &#x1f3ac; 个人…
阅读更多...
Azure Machine Learning - Azure OpenAI 服务使用 GPT-35-Turbo and GPT-4

Azure Machine Learning - Azure OpenAI 服务使用 GPT-35-Turbo and GPT-4

通过 Azure OpenAI 服务使用 GPT-35-Turbo and GPT-4 环境准备 Azure 订阅 - 免费创建订阅已在所需的 Azure 订阅中授予对 Azure OpenAI 服务的访问权限。 目前&#xff0c;仅应用程序授予对此服务的访问权限。 可以填写 https://aka.ms/oai/access 处的表单来申请对 Azure Op…
阅读更多...
基于PicGo实现Typora图片自动上传GitHub

基于PicGo实现Typora图片自动上传GitHub

文章目录 一. 引言二. 原理三. 配置3.1 GitHub 设置3.2 下载配置 PicGo3.3 配置 Typora3.4 使用 一. 引言 Typora是一款非常好的笔记软件&#xff0c;但是有一个比较不好的地方&#xff1a;默认图片是存放在本地缓存中。这就会导致文件夹一旦被误删或电脑系统重装而忘记备份文件…
阅读更多...
vr建筑虚拟实景展厅漫游体验更直观全面

vr建筑虚拟实景展厅漫游体验更直观全面

随着科技的不断进步&#xff0c;纯三维、可交互、轻量化的三维线上展览云平台&#xff0c;打破时间界限&#xff0c;以其独特的魅力&#xff0c;给予客户更多的自主性、趣味性和真实性&#xff0c;客户哪怕在天南地北&#xff0c;通过网络、手机即可随时随地参观企业线上立体化…
阅读更多...
多元线性回归（一）

多元线性回归（一）

基本概念 线性回归时机器学习中监督学习下的一种算法。回归问题主要关注是因变量&#xff08;需要预测的值&#xff0c;可以是一个也可以是多个&#xff09;和一个或多个值型的自变量&#xff08;预测变量&#xff09;之间的关系。 需要预测的值&#xff1a;即目标变量&#x…
阅读更多...
聚观早报 |东方甄选将上架文旅产品；IBM首台模块化量子计算机

聚观早报 |东方甄选将上架文旅产品；IBM首台模块化量子计算机

【聚观365】12月6日消息 东方甄选将上架文旅产品 IBM首台模块化量子计算机 新思科技携手三星上新兴领域 英伟达与软银推动人工智能研发 苹果对Vision Pro供应商做出调整 东方甄选将上架文旅产品 东方甄选宣布12月10日将在东方甄选APP上线文旅产品&#xff0c;受这一消息影…
阅读更多...
idea+spring框架+thymeleaf实现数据库增加数据（不使用xml文件）

idea+spring框架+thymeleaf实现数据库增加数据（不使用xml文件）

增加数据主要涉及四个文件 Apple.java写清楚数据库内部字段 package com.example.appledemo.pojo;import lombok.Getter;Getter public class Apple {private Integer appleId;private Integer price;private Integer weight;public void setAppleId(Integer appleId) {this.a…
阅读更多...
合并PDF（将多个pdf文件整合成一个pdf文件）

合并PDF（将多个pdf文件整合成一个pdf文件）

推荐使用下面这个免费在线的PDF文件合并工具&#xff0c;简单且易操作。 合并PDF - 在线上免费合并PDF文件 (smallpdf.com) 还有其他功能&#xff0c;不过现在我尚未使用其他功能&#xff1a; 关于费用&#xff1a;
阅读更多...
工厂方法设计模式项目实践

工厂方法设计模式项目实践

前言 以采集数据处理逻辑为例&#xff0c;数据采集分为不同种类如&#xff1a;MQTT、MODBUS、HTTP等&#xff0c;不同的采集数据有不同的解析处理逻辑。但总体解析处理步骤是固定的。可以使用工厂方法设计模式简化代码&#xff0c;让代码变得更加优雅。 代码实战 抽象类 总体…
阅读更多...
反序列化 [网鼎杯 2020 朱雀组]phpweb 1

反序列化 [网鼎杯 2020 朱雀组]phpweb 1

打开题目 我们发现这个页面一直在不断的刷新 我们bp抓包一下看看 我们发现index.php用post方式传了两个参数上去&#xff0c;func和p 我们需要猜测func和p两个参数之间的关系&#xff0c;可以用php函数MD5测一下看看 我们在响应处得到了一串密文&#xff0c;md5解密一下看看 发…
阅读更多...
Vue+ElementUI技巧分享：结合Sortablejs实现表格行拖拽

Vue+ElementUI技巧分享：结合Sortablejs实现表格行拖拽

文章目录 前言准备工作示例代码代码说明1. 引入依赖和组件结构2. 组件数据和生命周期3. 实现拖拽功能4. 更新数据和服务器同步 运行效果总结 前言 在很多动态网页应用中&#xff0c;用户界面的交互性是提高用户体验的关键。在 Vue.js 中&#xff0c;结合 Element UI 和 sortab…
阅读更多...
为何开展数据清洗、特征工程和数据可视化、数据挖掘与建模？

为何开展数据清洗、特征工程和数据可视化、数据挖掘与建模？

1.2为何开展数据清洗、特征工程和数据可视化、数据挖掘与建模 视频为《Python数据科学应用从入门到精通》张甜 杨维忠 清华大学出版社一书的随书赠送视频讲解1.2节内容。本书已正式出版上市&#xff0c;当当、京东、淘宝等平台热销中&#xff0c;搜索书名即可。内容涵盖数据科学…
阅读更多...
【Linux】冯诺依曼体系结构（硬件）、操作系统（软件）、系统调用和库函数 --- 概念篇

【Linux】冯诺依曼体系结构（硬件）、操作系统（软件）、系统调用和库函数 --- 概念篇

&#x1f466;个人主页&#xff1a;Weraphael ✍&#x1f3fb;作者简介&#xff1a;目前正在学习c和Linux还有算法 ✈️专栏&#xff1a;Linux &#x1f40b; 希望大家多多支持&#xff0c;咱一起进步&#xff01;&#x1f601; 如果文章有啥瑕疵&#xff0c;希望大佬指点一二 …
阅读更多...
微信小程序 分享的两种方式：菜单级和按钮级

微信小程序 分享的两种方式：菜单级和按钮级

按钮级 在使用微信小程序的时候&#xff0c;我们可能会设计到一些视频的一些分享等&#xff0c;那么视频分享也分为两种方式,例如下图&#xff0c;当我们点击的时候&#xff0c;进行一个转发分享的一个操作 那么在原先代码的基础上&#xff0c;我们需要在原先代码的基础上butt…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023