创作目的：为了方便自己后续复习重点，以及养成写博客的习惯。

组合和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

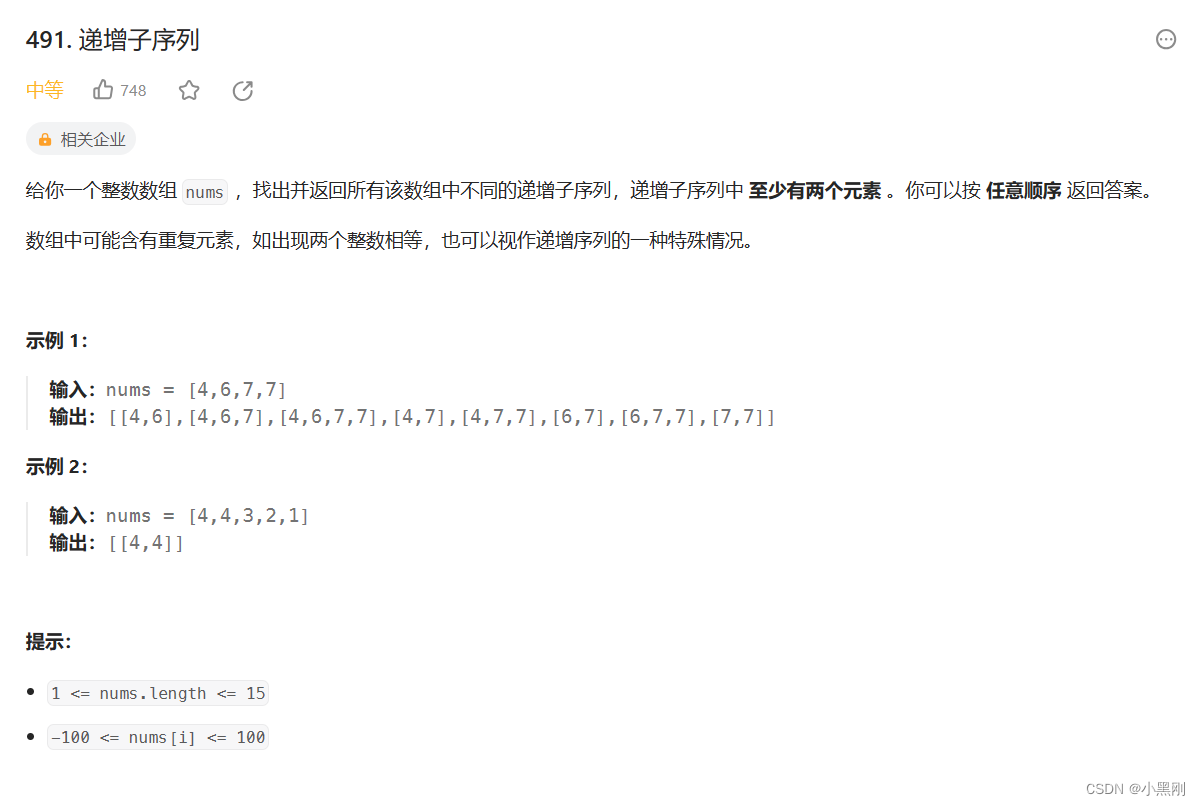
一、递增子序列

思路：参考carl文档

        已经是递增序列故而不用排序，元素不能重复使用，需要startIndex，调整下一层递归的起始位置。在遍历树形结构找每一个节点，可以通过startIndex结束递归，可以不加终止条件。通过树形结构了解到，同一层元素使用过就不能再使用了。

ledcode题目：https://leetcode.cn/problems/non-decreasing-subsequences/

AC代码：

int* path;
int pathTop;
int** ans;
int ansTop;
int* length;
//将当前path中的内容复制到ans中
void copy() {
    int* tempPath = (int*)malloc(sizeof(int) * pathTop);
    memcpy(tempPath, path, pathTop * sizeof(int));
    length[ansTop] = pathTop;
    ans[ansTop++] = tempPath;
}

//查找uset中是否存在值为key的元素
int find(int* uset, int usetSize, int key) {
    int i;
    for(i = 0; i < usetSize; i++) {
        if(uset[i] == key)
            return 1;
    }
    return 0;
}

void backTracking(int* nums, int numsSize, int startIndex) {
    //当path中元素大于1个时，将path拷贝到ans中
    if(pathTop > 1) {
        copy();
    }
    int* uset = (int*)malloc(sizeof(int) * numsSize);
    int usetTop = 0;
    int i;
    for(i = startIndex; i < numsSize; i++) {
        //若当前元素小于path中最后一位元素 || 在树的同一层找到了相同的元素，则continue
        if((pathTop > 0 && nums[i] < path[pathTop - 1]) || find(uset, usetTop, nums[i]))
            continue;
        //将当前元素放入uset
        uset[usetTop++] = nums[i];
        //将当前元素放入path
        path[pathTop++] = nums[i];
        backTracking(nums, numsSize, i + 1);
        //回溯
        pathTop--;
    }
}

int** findSubsequences(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    //辅助数组初始化
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(sizeof(int*) * 33000);
    length = (int*)malloc(sizeof(int*) * 33000);
    pathTop = ansTop = 0;

    backTracking(nums, numsSize, 0);

    //设置数组中返回元素个数，以及每个一维数组的长度
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = length[i];
    }
    return ans;
}

二、全排列

思路：参考carl文档

        处理排列问题就不需要使用startIndex而是需要一个used数组，标记已经选元素。当收集元素的数组path的大小和nums数组一样大时，说明找到了一个全排列，也表示到达了叶子节点。排列问题每次都要从头开始搜索，used数组就是记录path里有哪些元素使用了，一个排列里一个元素只能使用一次。

lecode题目：https://leetcode.cn/problems/permutations/

AC代码：

int* path;
int pathTop;
int** ans;
int ansTop;

//将used中元素都设置为0
void initialize(int* used, int usedLength) {
    int i;
    for(i = 0; i < usedLength; i++) {
        used[i] = 0;
    }
}

//将path中元素拷贝到ans中
void copy() {
    int* tempPath = (int*)malloc(sizeof(int) * pathTop);
    int i;
    for(i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    ans[ansTop++] = tempPath;
}

void backTracking(int* nums, int numsSize, int* used) {
    //若path中元素个数等于nums元素个数，将nums放入ans中
    if(pathTop == numsSize) {
        copy();
        return;
    }
    int i;
    for(i = 0; i < numsSize; i++) {
        //若当前下标中元素已使用过，则跳过当前元素
        if(used[i])
            continue;
        used[i] = 1;
        path[pathTop++] = nums[i];
        backTracking(nums, numsSize, used);
        //回溯
        pathTop--;
        used[i] = 0;
    }
}

int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    //初始化辅助变量
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(sizeof(int*) * 1000);
    int* used = (int*)malloc(sizeof(int) * numsSize);
    //将used数组中元素都置0
    initialize(used, numsSize);
    ansTop = pathTop = 0;

    backTracking(nums, numsSize, used);

    //设置path和ans数组的长度
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; i++) {
        (*returnColumnSizes)[i] = numsSize;
    }
    return ans;
}

三、全排列II

思路：参考carl文档

         与全排列的区别在于给定一个可重复数字的序列，要返回所有不重复的全排列(去重)。而且去重一定要对元素进行排序，通过相邻的节点来判断元素是否重复使用了。     同一树层的前一位（nums[i-1]）如果使用过，那么就进行去重。

ledcode题目：https://leetcode.cn/problems/permutations-ii/description/

AC代码：

//临时数组
int *path;
//返回数组
int **ans;
int *used;
int pathTop, ansTop;

//拷贝path到ans中
void copyPath() {
    int *tempPath = (int*)malloc(sizeof(int) * pathTop);
    int i;
    for(i = 0; i < pathTop; ++i) {
        tempPath[i] = path[i];
    }
    ans[ansTop++] = tempPath;
}

void backTracking(int* used, int *nums, int numsSize) {
    //若path中元素个数等于numsSize，将path拷贝入ans数组中
    if(pathTop == numsSize)
        copyPath();
    int i;
    for(i = 0; i < numsSize; i++) {
        //若当前元素已被使用
        //或前一位元素与当前元素值相同但并未被使用
        //则跳过此分支
        if(used[i] || (i != 0 && nums[i] == nums[i-1] && used[i-1] == 0))
            continue;

        //将当前元素的使用情况设为True
        used[i] = 1;
        path[pathTop++] = nums[i];
        backTracking(used, nums, numsSize);
        used[i] = 0;
        --pathTop;
    }
}

int cmp(void* elem1, void* elem2) {
    return *((int*)elem1) - *((int*)elem2);
}

int** permuteUnique(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    //排序数组
    qsort(nums, numsSize, sizeof(int), cmp);
    //初始化辅助变量
    pathTop = ansTop = 0;
    path = (int*)malloc(sizeof(int) * numsSize);
    ans = (int**)malloc(sizeof(int*) * 1000);
    //初始化used辅助数组
    used = (int*)malloc(sizeof(int) * numsSize);
    int i;
    for(i = 0; i < numsSize; i++) {
        used[i] = 0;
    }

    backTracking(used, nums, numsSize);

    //设置返回的数组的长度
    *returnSize = ansTop;
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int z;
    for(z = 0; z < ansTop; z++) {
        (*returnColumnSizes)[z] = numsSize;
    }
    return ans;
}

全篇后记：

        在明确思路的前提下，才能开始做，不然总会去走回头路。