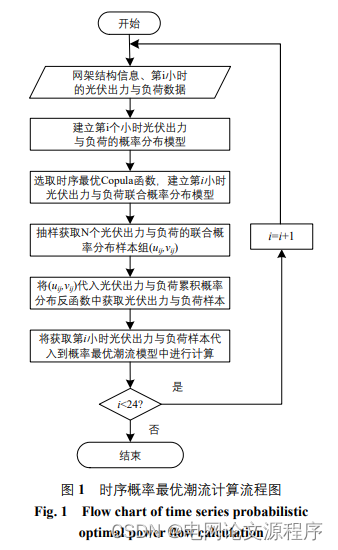
文章解读与仿真程序复现思路——中国电机工程学报EI\CSCD\北大核心《基于自适应扩散核密度估计的时序相关概率最优潮流计算方法》

这个标题涉及到电力系统中潮流计算的一种方法，具体解读如下：

概述：
- 时序相关概率最优潮流计算方法： 这是一种电力系统中潮流计算的方法，其中考虑了时序（时间序列）和概率的相关性。概率最优潮流通常是指在考虑不确定性和随机性的情况下，通过概率模型来计算电力系统中的潮流分布。
方法基础：
- 自适应扩散核密度估计： 该方法的基础是自适应扩散核密度估计。核密度估计是一种非参数统计方法，用于估计随机变量的概率密度函数。自适应扩散核密度估计可能表示在估计中使用了一种能够适应数据分布变化的扩散核，这样可以更好地捕捉复杂的概率密度形状。
关键特征：
- 时序相关性： 方法考虑了电力系统中变量随时间变化的关系。这可能涉及到对电力系统状态进行连续的时间观察和建模，以更好地反映系统动态性。
- 概率优化： 方法通过概率模型进行优化，考虑了不确定性因素对潮流计算的影响。这可以帮助系统规划者更全面地理解系统潮流的概率性质，从而做出更为可靠的决策。
应用领域：
- 这样的方法可能在电力系统规划、操作和市场运营等方面发挥作用。通过考虑时序相关性和概率性，可以更准确地评估电力系统的稳定性和可靠性，有助于系统的合理运营和规划。
研究创新点：
- 该方法的创新点可能在于将自适应扩散核密度估计引入时序相关概率最优潮流计算中，以提高对系统动态性和不确定性的建模精度。

总体而言，这个标题描述了一种结合了自适应扩散核密度估计、时序相关性和概率最优化的潮流计算方法，该方法有望提高电力系统潮流计算的准确性和可靠性。

摘要：为准确评估光伏与负荷的时序性和相关性对电力系统运行状态的影响,提出一种基于自适应扩散核密度估计的时序相关概率最优潮流计算方法。首先,利用光伏出力的自适应扩散核密度估计模型将高斯核函数转换为线性扩散过程,采用渐进积分误差法(asymptotic mean integrated squared error,AMISE)为扩散核函数选取自适应最优带宽,提高了光伏出力模型的局部适应性;其次,利用Copula理论构建光伏与负荷的时序联合概率分布模型,并获取具有相关性的时序光伏出力与负荷样本,进而提出能够准确计及光伏与负荷时序性和相关性的概率最优潮流计算方法;最后基于我国某地光伏电站实测数据与IEEE30节点系统进行仿真分析,验证了所提出计及光伏出力与负荷时序相关性的概率最优潮流计算方法的准确性与有效性。

这段摘要描述了一种用于电力系统的潮流计算方法，着重考虑了光伏发电和负荷时序性以及它们之间的相关性。以下是对摘要各部分的详细解读：

问题陈述：
- 背景： 摘要的开头指出了一个问题，即光伏和负荷的时序性和相关性对电力系统运行状态产生的影响。这表明作者关注于考虑可再生能源（光伏）和电力需求（负荷）的变化对电力系统的影响。
方法提出：
- 基于自适应扩散核密度估计的时序相关概率最优潮流计算方法： 作者提出了一种方法，采用自适应扩散核密度估计，以考虑光伏出力的时序性。这种方法被设计为能够同时考虑光伏和负荷之间的相关性，从而更全面地评估电力系统的运行状态。
方法细节：
- 光伏出力模型改进： 通过自适应扩散核密度估计模型，将高斯核函数转换为线性扩散过程。使用渐进积分误差法（AMISE）为扩散核函数选择自适应最优带宽，以提高光伏出力模型的局部适应性。
- Copula理论应用： 利用Copula理论构建了光伏和负荷的时序联合概率分布模型，获取具有相关性的时序光伏出力与负荷样本。Copula理论是用于建模随机变量之间依赖关系的方法，因此能够更准确地反映光伏和负荷之间的相关性。
仿真与验证：
- 仿真分析： 作者使用我国某地光伏电站实测数据和IEEE30节点系统进行仿真分析。这表示作者不仅提出了一种新方法，而且还在实际数据和标准电力系统模型上进行了验证。
- 验证结果： 通过仿真，作者验证了所提出的考虑光伏出力与负荷时序相关性的概率最优潮流计算方法的准确性与有效性。

综合而言，这项研究的创新之处在于将自适应扩散核密度估计和Copula理论相结合，提出了一种更全面考虑光伏和负荷时序性与相关性的潮流计算方法，并通过仿真验证了其准确性。

关键词:自适应扩散核;光伏出力;时序性与相关性; Copula理论; 概率最优潮流;

自适应扩散核 (Adaptive Diffusion Kernel):
- 这指的是一种用于估计概率密度函数的方法，其中核函数（通常是高斯核函数）的扩散参数是自适应的。在这里，它似乎被应用于改进光伏出力模型，以更好地捕捉其时序性。
光伏出力 (Photovoltaic Output):
- 这是指光伏发电系统的产出电能，通常是由太阳能光伏板转换太阳辐射为电能的结果。在这个上下文中，关注光伏出力的时序性，即它如何随时间变化。
时序性与相关性 (Temporal and Correlation):
- 这表明研究关注了时间序列数据的特征，即数据随时间的变化。而且，它还关注了不同数据（可能是光伏出力和负荷）之间的相关性，即它们之间是否存在某种关联关系。
Copula理论 (Copula Theory):
- Copula理论是用于建模随机变量之间依赖结构的数学工具。在这里，它被用来构建光伏和负荷的时序联合概率分布模型，以更准确地描述它们之间的相关性。
概率最优潮流 (Probabilistic Optimal Power Flow):
- 这是一种潮流计算方法，考虑到不确定性和概率分布。在这个上下文中，作者提出了一种方法，通过考虑自适应扩散核和Copula理论，实现了更准确地计算光伏和负荷对电力系统运行状态的影响的概率最优潮流。

这些关键词的结合表明研究的目标是通过考虑时序性和相关性，以概率的方式计算电力系统中光伏发电和负荷对系统状态的影响。这种方法的创新性在于采用了自适应扩散核和Copula理论，从而更好地处理了不同数据之间的复杂关系。

仿真算例：利用我国西北某地光伏电站 24:00 实测数据进行仿真，得到高斯核密度估计概率密度曲线及自适应扩散核密度估计概率密度曲线对比如图 2—4(以 9:00、13:00、17:00 为例)。图 2 中，非参数核密度估计法只能大致描述光伏出力 0~16MW 的概率分布趋势，对于 1~3MW、10~12MW 的曲线波峰以及 8~10MW 的曲线波谷的描述效果远逊于自适应扩散核密度估计法。在图 3 中，13h 的光伏出力概率密度曲线具有 3~5MW、15~19MW、22~25MW 3 个波峰，非参数核密度估计法均未能跟随，丢失了光伏出力概率密度分布的重要信息。图 4 中，光伏出力数据的波动性较小，峰谷波动较少，自适应扩散核密度对峰谷值的描述更接近实测数据。综上可知，相对于传统非参数核密度估计法，自适应扩散核密度估计曲线对一天中各个时段光伏出力实测数据均能取得更好的拟合效果，能够有效提高光伏出力概率密度曲线的局部适应性，更有效的反映光伏出力的不确定性与波动性。

仿真程序复现思路：

当构建仿真程序时，首先需要确保有足够的数据。假设你的数据是一个CSV文件，其中包含了时间和光伏出力的信息。下面是一个更详细的Python代码示例，用于读取数据、选择特定时刻的数据、进行高斯核密度估计，并绘制图形：

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde

# 步骤1：导入必要的库
# 如果没有安装这些库，可以使用 pip install numpy pandas seaborn matplotlib scipy 安装
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import gaussian_kde

# 步骤2：读取实测数据
# 假设CSV文件中有“时间”和“光伏出力”两列
data = pd.read_csv('your_data_file.csv')

# 步骤3：选择特定时刻的数据
# 假设你要选择的时刻是9:00、13:00和17:00
selected_times = ['09:00', '13:00', '17:00']
selected_data = data[data['时间'].isin(selected_times)]

# 步骤4：提取光伏出力数据
pv_output = selected_data['光伏出力'].values

# 步骤5：使用高斯核密度估计
kde = gaussian_kde(pv_output)
x_grid = np.linspace(0, pv_output.max(), 1000)  # 生成绘图用的坐标网格
pdf_estimate = kde(x_grid)

# 步骤6：绘制图形
plt.figure(figsize=(8, 6))
sns.lineplot(x=x_grid, y=pdf_estimate, label='高斯核密度估计')
sns.histplot(pv_output, bins=20, kde=False, color='gray', label='实测数据')

plt.xlabel('光伏出力 (MW)')
plt.ylabel('概率密度')
plt.title('高斯核密度估计 vs 实测数据')
plt.legend()
plt.show()

这个代码示例假设你有一个CSV文件，其中包含时间和光伏出力的数据。你可以根据实际情况调整列名和文件路径。此外，你可能需要安装缺失的库，你可以使用pip install命令安装它们。

这个代码展示了从数据读取到绘制图形的完整流程，希望这对你有帮助。