算法 搜索

news2024/11/24 7:42:07

深度优先搜索

广度优先搜索

深搜与广搜的区别

深搜 dfs——回溯——“不撞南墙不回头”

思路

总的来说是不撞南墙不回头，相当于一个人严格按照固定的行为模式。

例如走方格，依次走上下左右，每次走到一个新格子记录自己已经走过的方向，当到达终点或是所有方向走完之后，会重新回到上一格，代表上一格此方向【之前按照哪个方向到达此格的方向】的遍历完成。

形成效果

一个dfs其实是对一个问题的结果集的所有解题情况的遍历【不管这个解题情况是否复合题意】。

dfs 搜索树与回溯

一个dfs其实是对一个问题的结果集的所有解题情况的遍历，在遍历过程中，前面解题情况的选择会影响到后面的解题情况。

例如走迷宫，解题情况其实就是主人公走到哪个格子，他会影响到之后走过的路径。

所以我们其实可以将解题情况进行串联，将前面的选择作为一个图的前驱节点，而后面的结果作为后继节点，那么所有的解题情况的遍历便可以组成一个树，我们叫做搜索树。树上的根节点到 某个叶节点的一条路径就是一条解题过程。

那迷宫来进行距离，我们把主人公当前正在走的点当作前驱，而之后依照行为模式工作后所走到的下一个点作为后继。那么所有所走过的路径的集合便可构成一个树。

在dfs遍历解题结果的过程中，会存储并改变一些解题的状态，由于我们是会对所有情况依次进行遍历，当一种情况遍历完成后，dfs应该回到上一个节点进行行为模式的继续遍历。

例如迷宫，走到死胡同或者终点时，应该回到上一次走过的点，看其他方向能否到达终点。

注意，dfs是进行所有结果的遍历，所以在到达终点后并不会停止，而是会继续回到上一步运行。

而此时回到上一个节点就意味着，之前走过的一些点，在这个时刻应该是没有走过的，所以的话在写代码的时候应该进行一个状态的回溯。在回到上一个节点之前，本节点对于上一个节点应该是没有遍历过的，所以要进行状态改变。

代码模板

人走迷宫，迷宫情况使用0、1表示，1可行，0不可行。先给定起点与终点，求所有路径中最少要走多少格子。

递归实现

#include<stdio.h>
_Bool map[100][100] = { 0 };//1代表可行，0不可行
_Bool visit[100][100] = { 0 };//0未走，1走过
int mov[4][2] = { {0,1},{1,0},{0,-1},{-1,0} };//右下左上
int endx, endy, startx, starty;
int col, row, t;
_Bool can = 0;
int min = 0x3f3f3f3f;//代表正无穷
void dfs(int x,int y, int value) {//如果value没有被设为参数，回溯的时候需要改变value值
	if (value > min)//最优剪枝1
		return;
	if (x<0 || y<0 || x>=row || y>=col)//判断是否出界
		return;
	if (x == endx && y == endy) {//结束条件，找到终点
		can = 1;
		if (value < min)
			min = value;
		return;//回退，防止继续走下去，已经到达终点了，没必要再走了
	}
	if (value >= min)//最优剪枝2,未到达终点，便value=min，那么到达终点时，一定回value>min
		return;
	for (int i = 0;i < 4;i++) {
		int xx = x + mov[i][0], yy = y + mov[i][1];//人物偏移
		if (map[xx][yy] && !visit[xx][yy]) {//判断是否可以进入下一格，可行性剪枝
            visit[xx][yy] = 1;//先标记再访问
		    dfs(xx, yy, value+1);//让人物移动到下一格
		    visit[xx][yy] = 0;//回溯操作，当递归回到这一层的时候，(xx,yy)应该未访问，所以置为0
			//回溯操作是一层递归一层递归进行回溯，每次只会回溯到上一层，所以每次只用将当前位置的下一个操作的数据回溯
		}
		
	}
}
int main() {
	scanf("%d", &t);
	while (t--) {//t轮数据，每一次数据进行操作时，都要保证所有的状态都为最初状态，不被上一次操作所影响
		scanf("%d%d", &col, &row);
		for (int i = 0;i < row;i++)
			for (int j = 0;j < col;j++) {
				scanf("%d", &map[i][j]);
				visit[i][j] = 0;
			}
		scanf("%d%d%d%d", &startx, &starty, &endx, &endy);
		visit[startx][starty] = 1;
		dfs(startx, starty, 0);
		if (can)
			printf("能,min=%d\n", min);
		else
			printf("不能\n");
        _Bool can = 0;
	}
	return 0;
}

栈实现

#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
struct Point {
	int x, y, value, dir;
	Point(int a,int b,int value):x(a),y(b),value(value),dir(0){}
};
typedef struct Point TYPE;
int main(void) {
	stack<TYPE> Stack;//这个类可以用<>指定里面的内容的类型，类似于一个栈
	bool map[100][100] = { 0 }, visited[100][100] = { 0 };
	int mov[4][2] = { {0,1},{0,-1},{1,0},{-1,0} };
	int m, n;
	cin >> m >> n;
	int i, j;
	for (i = 0;i < m;i++)
		for (j = 0;j < n; j++)
			cin >> map[i][j];
	int startx, starty, endx, endy;
	scanf("%d%d%d%d", &startx, &starty, &endx, &endy);
	Stack.emplace(startx, starty, 0);
	visited[startx][starty] = 1;
	while (!Stack.empty()) {//栈非空进行循环
		TYPE* cur = &Stack.top();
		if (cur->x == endx && cur->y == endy) {//判断是否到达终点
			printf("%d\n", cur->value);
			visited[cur->x][cur->y] = 0;
			Stack.pop();
			continue;//如果到达，弹栈，回到上一次位置，进行下一轮循环
		}
		if (cur->dir <= 3) {//遍历
			int xx = cur->x + mov[cur->dir][0];
			int yy = cur->y + mov[cur->dir][1];
			cur->dir++;//进入一个新的结点的时候，dir=0，当遍历之后要自增

			if (xx < m && yy < n && xx >= 0 && yy >= 0 && !visited[xx][yy] && !map[xx][yy]) {
				Stack.emplace(xx, yy, cur->value + 1);//压栈
				visited[xx][yy] = 1;
			}
		}
		else {//弹栈
			visited[cur->x][cur->y] = 0;
			Stack.pop();
		}
	}
	return 0;
}

与模板差异

  1. 是否回溯
  2. 遍历方向
  3. 结束条件
  4. 结束处理

超时后的解决方法

  1. 换思路：主要换遍历的方式【mov之类的】
  2. 剪枝

普通无回溯 dfs

例题

海战 - 洛谷

该题与走迷宫不同，走迷宫是从一个点为起点，然后一直走下去，每走完一种情况后需要回过头检查是否有其他路可走，需要进行回溯。该题是需要遍历每一个点，若该点是船只的一部分，需要判断该点是否可以与其它点相连构成船只，且每个点只能使用一次【使用过之后就不能再次使用】，走到头后，不需要回过头检查其他的路径，所以不需要回溯。

#include<stdio.h>
int	R, C, S = 0;
char map[1005][1005] = { 0 };
int mov[4][2] = { {-1,0},{1,0},{0,-1},{0,1} };
void dfs(int x, int y) {
	map[x][y] = '.';//因为每只船只能使用一次，所以在使用之后要将‘#’标记为‘.’，后期不可以再使用
	for (int i = 0;i < 4;i++) {
		int xx = x + mov[i][0], yy = y + mov[i][1];
		if (xx >= 0 && xx < R && yy >= 0 && yy < C && map[xx][yy] == '#') {
			dfs(xx, yy);
		}
	}
	return;
}
//判断船的位置是否合法，即在一个正方形中，四个角上如果有三个角有船就是不合理的，那样子会出现一个三角形，不是方形
_Bool d(int i, int j) {
	int c = 0;
	if (map[i][j] == '#')
	    c++;
	if (map[i + 1][j] == '#')
	    c++;
	if (map[i][j + 1] == '#')
	    c++;
	if (map[i + 1][j + 1] == '#')
	    c++;
	if (c == 3)
		return 0;
	return 1;
}
int main() {
	scanf("%d%d", &R, &C);
	for (int i = 0;i < R;i++) {
		scanf("%s", map[i]);
	}
	for (int i = 0;i < R;i++) {
		for (int j = 0;j < C;j++) {
			if (d(i, j) == 0) {
				printf("Bad placement.");
				return 0;
			}
		}
	}
	for (int i = 0;i < R;i++) {
		for (int j = 0;j < C;j++) {
			if (map[i][j] == '#') {
				S++;
				dfs(i, j);
			}
		}
	}
	printf("There are %d ships.", S);

	return 0;
}

剪枝

在搜索树中剪去多余枝干。

另一个结束递归的条件

  1. 可行性剪枝(判断可不可以走，包括有无障碍物和是否走过，……)
  2. 最优剪枝(消耗的能量，若目前未到终点，但是使用的能量已经超过min)
  3. 奇偶性剪枝
  4. 优化搜索顺序(人眼看)
  5. 冗余剪枝
  6. 记忆化搜索
  7. α-β剪枝(博弈算法，可能被人工智能使用)

优化搜索顺序

靠数学功底

可行性剪枝

就像上面的迷宫问题，能否走这个格子就是一个可行性剪枝。这个是根据题意来进行判断，看下一步路线是否可能符合题意，若直接违背则就不用走。

最优剪枝

适用于求最短路径

例题

[USACO2.1] 健康的荷斯坦奶牛 Healthy Holsteins - 洛谷

#include<stdio.h>
int v, g, need[30], food[20][30], ans[20], min = 0x3f3f3f3f, temp[20], len;//v所需要v种营养 g有g种饲料 need每种营养成分需要多少 food二维数组，低维:每种营养的含量，高维:饲料总类 ans答案数组 temp存储现在选择的饲料 len目前选了len种饲料 min做优情况，即选最少的种类便可达到所需的营养
_Bool visited[20];//状态数组，表示是否被选过
_Bool check(int len) {//检查是否达到所需的营养
	int nutrition[30] = { 0 };//每种营养现在的含量
	for (int i = 1;i <= len;i++) {
		for (int l = 1;l <= v;l++) {
			nutrition[l] += food[temp[i]][l];
		}	
	}
	for (int i = 1;i <= v;i++) {
		if (need[i] > nutrition[i])//只要有一种营养成分含量不合格，就返回0
			return 0;
	}
	return 1;
}
void dfs() {//搜索
    //最优剪枝
	if (len > g || len > min)//现在的饲料种类超过最优或超过总的饲料种类就退出递归
		return;
	if (check(len) == 1) {//检验是否达到所需的营养含量，若达到，与最优解进行比较，若所需的种类少于目前的最小的，则代替最小成为新的最少，即新的最优情况
		if (min > len) {
			min = len;
			for (int i = 1;i <= min;i++)
				ans[i] = temp[i];
		}
		return;
	}
	for (int i = temp[len]+1;i <= g;i++) {//遍历，注意遍历的开始是上一次选择下一个【遍历选择每一种饲料，不需要每次都从头开始选】
		if (!visited[i]) {
			visited[i] = 1;
			len++;
			temp[len] = i;
			dfs();
			visited[i] = 0;//回溯
			temp[len] = 0;
			len--;
		}
	}

}
int main() {
	scanf("%d", &v);
	for (int i = 1;i <= v;i++) {
		scanf("%d", &need[i]);
	}
	scanf("%d", &g);
	for (int i = 1;i <= g;i++) {
		for (int j = 1;j <= v;j++) {
			scanf("%d", &food[i][j]);
		}
	}
	dfs();
	printf("%d ", min);
	for (int i = 1;i <= min;i++)
		printf("%d ", ans[i]);
	return 0;
}

奇偶性剪枝

横纵坐标从1开始，横纵坐标相加为奇数赋为0，偶数赋为1

1->1:最近的1走两步，任何一个1走偶数步，0->0也是【同偶异奇】

冗余剪枝

重复的删除去

[USACO2.1] 健康的荷斯坦奶牛 Healthy Holsteins - 洛谷

#include<stdio.h>
int v, g, need[30], food[20][30], ans[20], min = 0x3f3f3f3f, temp[20], len;//v所需要v种营养 g有g种饲料 need每种营养成分需要多少 food二维数组，低维:每种营养的含量，高维:饲料总类 ans答案数组 temp存储现在选择的饲料 len目前选了len种饲料 min做优情况，即选最少的种类便可达到所需的营养
_Bool visited[20];//状态数组，表示是否被选过
_Bool check(int len) {//检查是否达到所需的营养
	int nutrition[30] = { 0 };//每种营养现在的含量
	for (int i = 1;i <= len;i++) {
		for (int l = 1;l <= v;l++) {
			nutrition[l] += food[temp[i]][l];
		}	
	}
	for (int i = 1;i <= v;i++) {
		if (need[i] > nutrition[i])//只要有一种营养成分含量不合格，就返回0
			return 0;
	}
	return 1;
}
void dfs() {//搜索
    //最优剪枝
	if (len > g || len > min)//现在的饲料种类超过最优或超过总的饲料种类就退出递归
		return;
	if (check(len) == 1) {//检验是否达到所需的营养含量，若达到，与最优解进行比较，若所需的种类少于目前的最小的，则代替最小成为新的最少，即新的最优情况
		if (min > len) {
			min = len;
			for (int i = 1;i <= min;i++)
				ans[i] = temp[i];
		}
		return;
	}
	for (int i = temp[len]+1;i <= g;i++) {//遍历，注意遍历的开始是上一次选择下一个【遍历选择每一种饲料，不需要每次都从头开始选】
		if (!visited[i]) {
			visited[i] = 1;
			len++;
			temp[len] = i;
			dfs();
			visited[i] = 0;//回溯
			temp[len] = 0;
			len--;
		}
	}

}
int main() {
	scanf("%d", &v);
	for (int i = 1;i <= v;i++) {
		scanf("%d", &need[i]);
	}
	scanf("%d", &g);
	for (int i = 1;i <= g;i++) {
		for (int j = 1;j <= v;j++) {
			scanf("%d", &food[i][j]);
		}
	}
	dfs();
	printf("%d ", min);
	for (int i = 1;i <= min;i++)
		printf("%d ", ans[i]);
	return 0;
}

记忆化搜索

将之前计算的结果存储在数组中，当计算同样的数据时，可以直接使用之前计算过的答案。

冗余：重复的直接被删除

记忆化搜索：借用之前重复的数据，而不是舍去

(x,y) data[x][y]

dfs(x,y)

if(data[x][y]算过){

return data[x][y];

}

dfs函数返回值类型不是void

使用条件

1.有限个 2.有重复值

例题

int dp[25][25][25];

int dfs(int a, int b, int c) {

if (a <= 0 || b <= 0 || c <= 0)

return 1;

if (a > 20 || b > 20 || c > 20) {

return dfs(20, 20, 20);

}

if (dp[a][b][c]) //先判断该值是否计算过，如果算过，直接调结果，不需要再次计算，直接返回即可

return dp[a][b][c];

if (a < b && b < c) {

dp[a][b][c] = dfs(a, b, c - 1) + dfs(a, b - 1, c - 1) - dfs(a, b - 1, c);

}

else

dp[a][b][c] = dfs(a - 1, b, c) + dfs(a - 1, b - 1, c) + dfs(a - 1, b, c - 1) - dfs(a - 1, b - 1, c - 1);

return dp[a][b][c];

}

例题——全排列

给定一个整数 n，将数字 1∼n 排成一排，将会有很多种排列方法。

现在，请你按照字典序将所有的排列方法输出。

输入格式

共一行，包含一个整数 n。

输出格式

按字典序输出所有排列方案，每个方案占一行。

数据范围

1≤n≤7

输入样例

3

输出样例

1 2 3

1 3 2

2 1 3

2 3 1

3 1 2

3 2 1

#include<stdio.h>
int n;
int a[10],state[10]={0};
void dfs(int step){
    if(step==n+1){
        for(int i=1;i<=n;i++)
            printf("%d ",a[i]);
        printf("\n");
        return;
    }
    for(int i=1;i<=n;i++){
        if(state[i]==0){
            a[step]=i;
            state[i]=1;
            dfs(step+1);
            a[step]=0;
            state[i]=0;
        }
    }
    return; 
}
int main(){
    scanf("%d",&n);
    dfs(1);
    return 0;
}

例题——八皇后

[USACO1.5] 八皇后 Checker Challenge - 洛谷

n*n的正方形，i表示行，j表示列，i+j表示其中一条对角线，i-j+n表示另外一条对角线

#include<stdio.h>
int a[15]={0},b[15]={0},c[30]={0},d[30]={0};
int n,sum=0;
void dfs(int i){
    if(i>n){
        if(sum<3){
            for(int k=1;k<=n;k++){
                printf("%d ",a[k]);
            }
            printf("\n");
        }
        sum++;
        return;
    }
    for(int j=1;j<=n;j++){
        if((!b[j])&&(!c[i+j])&&(!d[i-j+n])){
            a[i]=j;//行，第i行是第j个
            b[j]=1;//列
            c[i+j]=1;//对角线1,根据截距给对角线命名
            d[i-j+n]=1;//对角线2
            dfs(i+1);
            b[j]=0;//回溯
            c[i+j]=0;
            d[i-j+n]=0;
        }
    }
}
int main(){
    scanf("%d",&n);
    dfs(1);
    printf("%d",sum);
    return 0;
}

广搜 bfs——一层一层走

一层一层搜索，首先，先把所有第一层的点，即距离为1的点搜完，然后进入下一层，直到搜完。

边权相同时，可以用bfs求最短路。

实现思路

使用队列来实现，每次将要搜索的点放在队列中，刚开始搜索时，队列中只有一个点，然后每次将所有与队头元素相连的且没有访问过的，符合条件的点都放入队列，之后对 队头元素进行处理然后出队。当队列为空则说明搜索停止。

这样就可以保证一层一层遍历，遍历整体深度逐渐增大。

而由这样遍历出来的合法路径，若是两点间权值相同的话，是具有最优性质的。

框架

queue 初始状态

while queue 不空

{

t<--每次取队头

扩展队头t

}

例题——走迷宫

给定一个n*m的二维整数数组，用来表示一个迷宫，数组中只包含0或1，其中0表示可以走的路，1表示不可通过的墙壁。

最初，有一个人位于左上角(1, 1)处，已知该人每次可以向上、下、左、右任意一个方向移动一个位置。

请问，该人从左上角移动至右下角(n, m)处，至少需要移动多少次。

数据保证(1, 1)处和(n, m)处的数字为0，且一定至少存在一条通路。

输入格式

第一行包含两个整数n和m。

接下来n行，每行包含m个整数（0或1），表示完整的二维数组迷宫。

输出格式

输出一个整数，表示从左上角移动至右下角的最少移动次数。

数据范围

1≤n,m≤100

输入样例

5 5

0 1 0 0 0

0 1 0 1 0

0 0 0 0 0

0 1 1 1 0

0 0 0 1 0

输出样例

8

//bfs，使用手写队列实现
//输出路径，只需要再开一个数组prev，记录这个点是由那个点扩展出来即可
#include<iostream>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
const int N = 110;
int n, m;
char map[N][N];
int len[N][N];//每个点到起点的距离
PII q[N * N];//实现队列
//PII Prev[N][N];  //输出路径
int bfs() {
    int hh = 0, tt = 0;
    q[0] = { 0,0 };
    memset(len, -1, sizeof len);
    //初始化函数，将某一块内存中的内容全部设置为指定的值，通常为新申请的内存做初始化工作
    //参数1，指针或数组；参数2，赋给参数1的值；参数3，参数1的长度
    len[0][0] = 0;
    int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 };
    while (hh <= tt) {
        auto t = q[hh++];//每次取出队头元素
        for (int i = 0;i < 4;i++) {
            int x = t.first + dx[i], y = t.second + dy[i];
            if (x >= 0 && x < n && y >= 0 && y < m && map[x][y] == '0' && len[x][y] == -1) {
                len[x][y] = len[t.first][t.second] + 1;
                //Prev[x][y] = t;
                q[++tt] = { x,y };//在队尾插入元素
            }
        }
    }
    /*int x = n - 1, y = m - 1;
    while (x || y) {
    cout << x << ' ' << y << endl;
    auto t = Prev[x][y];
    x = t.first, y = t.second;
    }*/
    return len[n - 1][m - 1];
}
int main() {
    cin >> n >> m;
    for (int i = 0;i < n;i++)
        cin >> map[i];
    cout << bfs() << endl;
    return 0;
}

有向图的遍历

宽度优先遍历

一层一层搜索

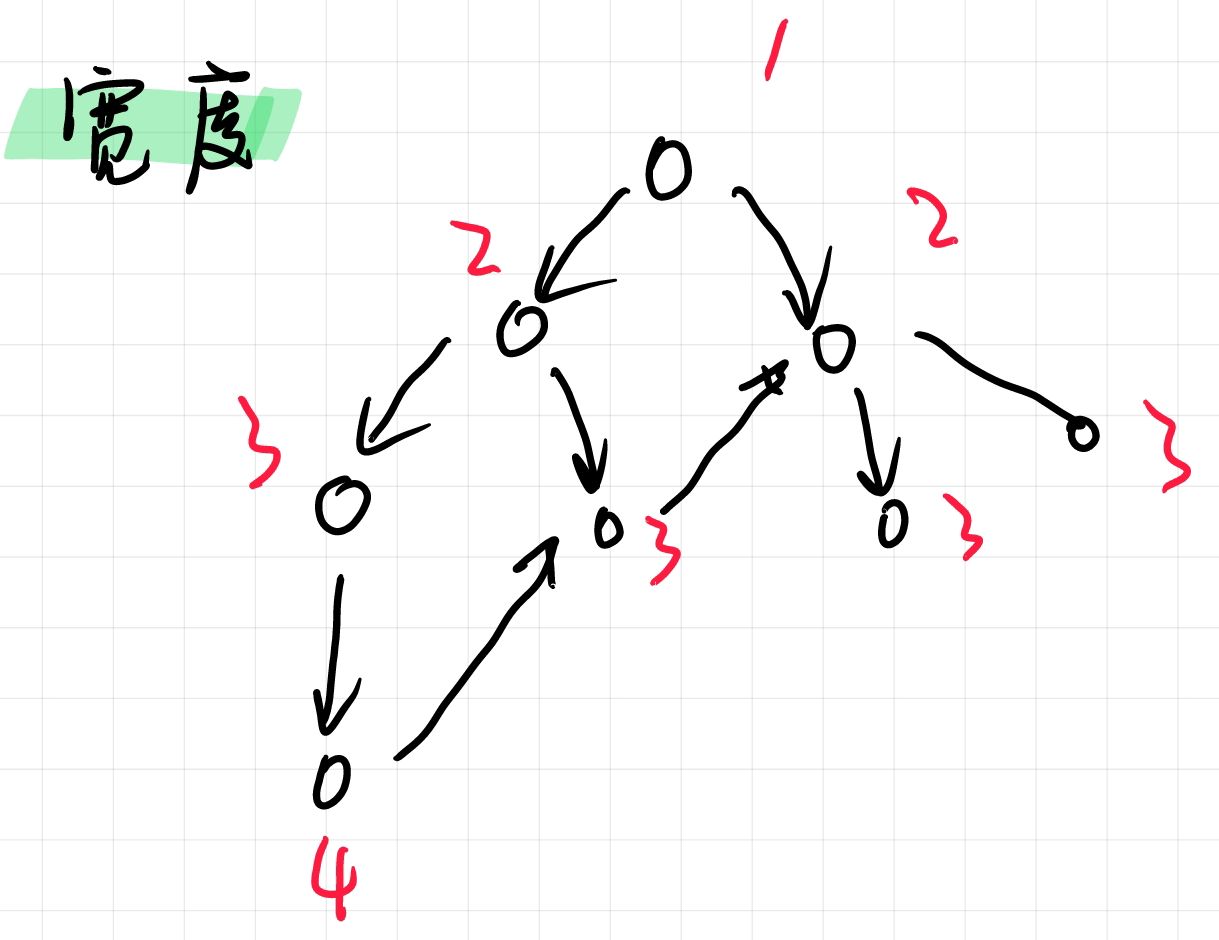
框架

queue ＜——　将起始状态插入队列中，即将1号点插入队列

while （queue 不空）{

t 每次取队头元素

拓展 t 所有能到的点 x

if（x 未被遍历）{

　queue <——x 将 x 入队

d[x]=d[t]+1

}

}

例题——图中点的层次

给定一个n个点m条边的有向图，图中可能存在重边和自环。

所有边的长度都是1，点的编号为1~n。

请你求出1号点到n号点的最短距离，如果从1号点无法走到n号点，输出-1。

输入格式

第一行包含两个整数n和m。

接下来m行，每行包含两个整数a和b，表示存在一条从a走到b的长度为1的边。

输出格式

输出一个整数，表示1号点到n号点的最短距离。

数据范围

1≤n,m≤10^5

输入样例

4 5

1 2

2 3

3 4

1 3

1 4

输出样例

1

代码

#include<iostream>
#include<cstring>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N];
void add(int a, int b) {//插入函数
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
int bfs() {
	int hh = 0, tt = 0;
	q[0] = 1;
	memset(d, -1, sizeof d);//初始化距离，-1代表未被初始化
	d[1] = 0;
	while (hh <= tt) {//判断队列是否为空
		int t = q[hh++];//取队头
		for (int i = h[t];i != -1;i = ne[i]) {//扩展队头
			int j = e[i];
			if (d[j] == -1) {
				d[j] = d[t] + 1;
				q[++tt] = j;
			}
		}
	}
	return d[n];
}
int main() {
	cin >> n >> m;
	memset(h, -1, sizeof h);//初始化表头
	for (int i = 0;i < m;i++) {
		int a, b;
		cin >> a >> b;
		add(a, b);
	}
	cout << bfs() << endl;
}

深度优先遍历

找到一个起点，然后从这个 起点开始，一条路走向黑

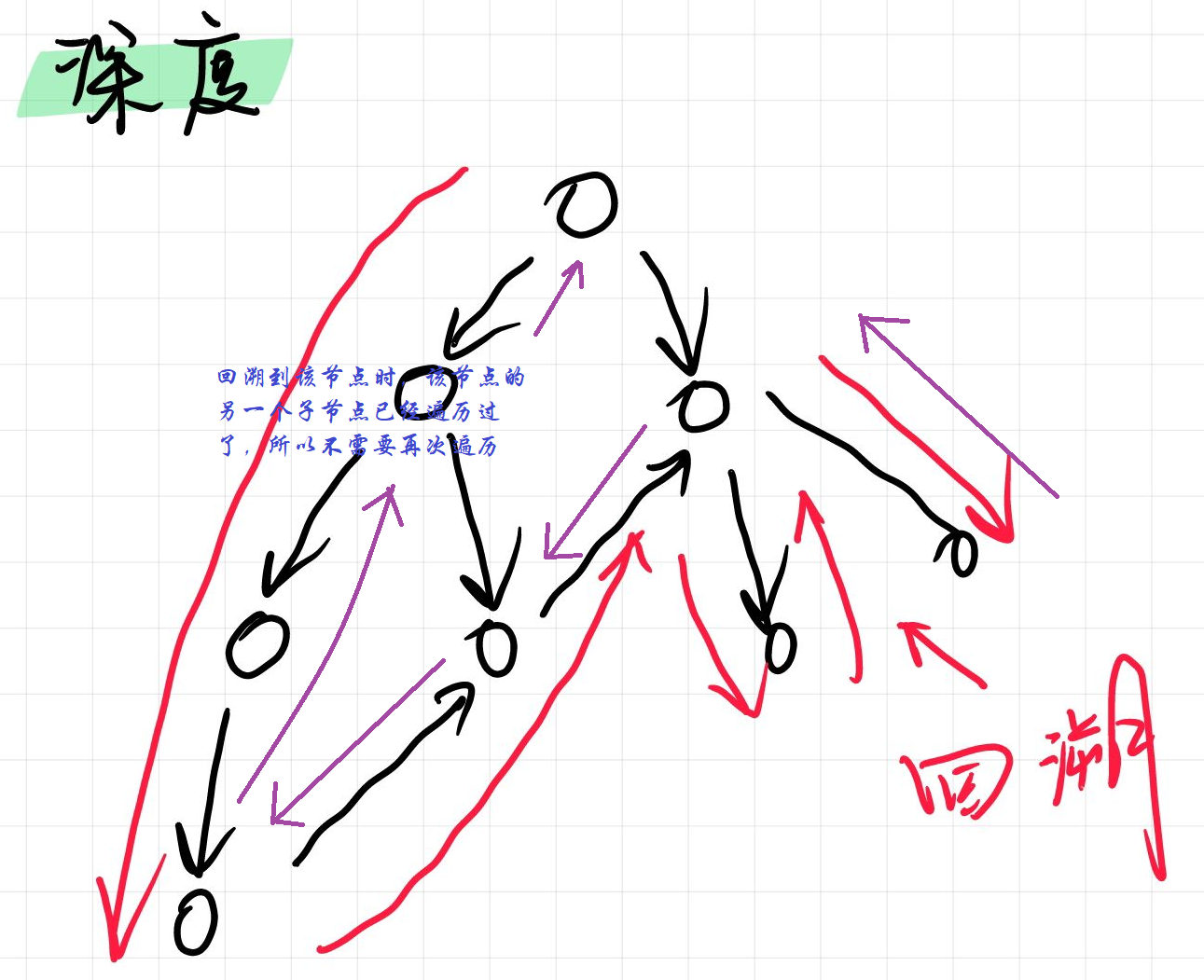
邻接表的深度优先遍历

主函数：

for(int i=0;i<n;i++) dfs(i); //枚举起点

dfs：

利用图中结点的编号进行搜索，e存图中结点的编号

int h[N], e[M], ne[M], idx;//h存n个链表的链表头，e存每个结点的值是多少，ne存每个结点的next值

bool st[N];

//树和图的深度优先搜索

void dfs(int u) {//u是当前dfs到的点

st[u] = true;//标记一下，已经被搜过了

for (int i = h[u];i != -1;i = ne[i]) {//遍历u的所有出边

int j = e[i];//链表中该点在图中的编号

if (!st[j])//如果j没有被搜过，那么就进行搜索

dfs(j);

}

例题——树的重心

给定一颗树，树中包含n个结点（编号1~n）和n-1条无向边【无向图】。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数n，表示树的结点数。

接下来n-1行，每行包含两个整数a和b，表示点a和点b之间存在一条边。

输出格式

输出一个整数m，表示重心的所有的子树中最大的子树的结点数目。

数据范围

1≤n≤10^5

输入样例

9

1 2

1 7

1 4

2 8

2 5

4 3

3 9

4 6

输出样例

4

代码

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1288130.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

亿胜盈科ATR2037 无限射频前端低噪声放大器

亿胜盈科ATR2037 无限射频前端低噪声放大器

亿胜盈科ATR2037 是一款应用于无线通信射频前端&#xff0c;工作频段为 0.7 到 6GHz 的超低噪声放大器。 ATR2037 低噪声放大器采用先进的 GaAs pHEMT 工艺设计和制作&#xff0c;ATR2037 低噪声放大器在整个工作频段内可以获得非常好的射频性能超低噪声系数。 亿胜盈科ATR203…
阅读更多...
班级查分软件制作教程：老师必备技能！

班级查分软件制作教程：老师必备技能！

首先&#xff0c;你需要选择一个合适的软件平台来制作班级查分软件。推荐使用群发成绩&#xff0c;因为它是一个功能强大且易于使用的在线查询系统&#xff0c;可以帮助你快速高效地制作班级查分软件​。 在制作班级查分软件之前&#xff0c;你需要准备好学生的成绩数据。这可以…
阅读更多...
云原生的 CI/CD 框架tekton - pipeline（一）

云原生的 CI/CD 框架tekton - pipeline（一）

文章目录 1. 官方介绍2. 组件2.1 Tekton Pipelines2.2 部署pipeline2.3 部署dashborad2.3.1 task2.3.2 taskrun2.3.3 Pipeline2.3.4 PipelineRun 3. 案例案例1: 拉取代码并查看readmestep1: 创建task - 拉取代码step2: 创建task - 查看reamdestep3: 创建task的编排 - pipelines…
阅读更多...
函数递归。

函数递归。

文章目录 前言一、什么是递归二、递归的限制条件三、递归举例1.求n的阶乘2. 举例2&#xff1a;顺序打印一个整数的每一位 四、递归的优劣总结 前言 不多废话了&#xff0c;直接开始。 一、什么是递归 递归是学习C语言函数绕不开的⼀个话题&#xff0c;那什么是递归呢&#xf…
阅读更多...
桥接网卡绑定

桥接网卡绑定

目录 1、创建一个桥接设备和会话 2、配置软件桥接网卡的IP地址、网关和地址获取方式 3、添加从设备和会话到桥接设备 4、启动从设备会话 5、启动桥接会话 ​ 桥接就是把一台机器上的若干个网络接口连接起来&#xff0c;其结果是&#xff0c;其中一个网卡收到的…
阅读更多...
【Polar靶场WEB签到】

【Polar靶场WEB签到】

题目&#xff1a; <?phperror_reporting(0);$file $_GET[file];if(!isset($file))$file 1;$file str_replace(../, , $file);include_once($file.".php");highlight_file(__FILE__); ?>解答&#xff1a;1、进入index页面&#xff0c;说让你加弟弟&#x…
阅读更多...
LeetCode：2477. 到达首都的最少油耗（DFS C++、Java）

LeetCode：2477. 到达首都的最少油耗（DFS C++、Java）

目录 2477. 到达首都的最少油耗 题目描述&#xff1a; 实现代码与解析&#xff1a; dfs 2477. 到达首都的最少油耗 题目描述&#xff1a; 给你一棵 n 个节点的树&#xff08;一个无向、连通、无环图&#xff09;&#xff0c;每个节点表示一个城市&#xff0c;编号从 0 到 n…
阅读更多...
生鲜蔬果展示预约小程序作用是什么

生鲜蔬果展示预约小程序作用是什么

线下生鲜蔬果店非常多&#xff0c;对商家来说主要以同城生意为主&#xff0c;而在互联网电商的发展下&#xff0c;更多的商家会选择搭建私域商城进行多渠道的销售卖货和拓展&#xff0c;当然除了直接卖货外&#xff0c;还有产品纯展示或预约订购等需求。 但无论哪种模式&#…
阅读更多...
一：对爬虫的简单认识

一：对爬虫的简单认识

一&#xff1a;爬虫前导知识 1.爬虫引入&#xff1a; ​ 网络爬虫又称为网络蜘蛛&#xff1b;网络蚂蚁&#xff1b;网络机器人等&#xff0c;可以自动高效地从互联网的海量信息中浏览获取到我们感兴趣的信息&#xff0c;在浏览信息的时候需要按照我们制定的规则进行&#xff…
阅读更多...
【springboot】整合redis和定制化

【springboot】整合redis和定制化

1.前提条件:docker安装好了redis,确定redis可以访问 可选软件: 2.测试代码 (1)redis依赖 org.springframework.boot spring-boot-starter-data-redis (2)配置redis &#xff08;3&#xff09; 注入 Resource StringRedisTemplate stringRedisTemplate; 这里如果用Autowi…
阅读更多...
基于Java SSM框架实现汽车在线销售系统项目【项目源码+论文说明】

基于Java SSM框架实现汽车在线销售系统项目【项目源码+论文说明】

基于java的SSM框架实现汽车在线销售系统演示 摘要 21世纪的今天&#xff0c;随着社会的不断发展与进步&#xff0c;人们对于信息科学化的认识&#xff0c;已由低层次向高层次发展&#xff0c;由原来的感性认识向理性认识提高&#xff0c;管理工作的重要性已逐渐被人们所认识&a…
阅读更多...
4 STM32MP1 Linux系统启动过程

4 STM32MP1 Linux系统启动过程

1. ROM代码 这是ST官方写的代码&#xff0c;在STM32MP1出厂时就已经烧录进去&#xff0c;不能被修改。ROM代码是上电以后首先执行的程序&#xff0c;它的主要工作就是读取STM32MP1的BOOT引脚电平&#xff0c;然后根据电平来判断当前启动设备&#xff0c;最后从选定的启动设备里…
阅读更多...
Educational Codeforces Round 159 (Rated for Div. 2) 之 A - E 题

Educational Codeforces Round 159 (Rated for Div. 2) 之 A - E 题

目录 [A. Binary Imbalance](https://codeforces.com/contest/1902/problem/A)DescriptionSolutionCode [B. Getting Points](https://codeforces.com/contest/1902/problem/B)DescriptionSolutionCode [C. Insert and Equalize](https://codeforces.com/contest/1902/problem/…
阅读更多...
C语言--每日选择题--Day37

C语言--每日选择题--Day37

第一题 1. 有以下说明语句&#xff1a;则下面引用形式错误的是&#xff08;&#xff09; struct Student {int num;double score; };struct Student stu[3] {{1001,80}, {1002,75}, {1003,91}} struct Student *p stu; A&#xff1a;p->num B&#xff1a;(p).num C&#…
阅读更多...
华为无线配置模板 一

华为无线配置模板 一

华为无线配置模板 一 拓扑图1.配置SwitchA和AC&#xff0c;使AP与AC之间能够传输CAPWAP报文2.配置AC作为DHCP服务器&#xff0c;为STA和AP分配IP地址3.配置AP上线4.配置WLAN业务参数5.验证配置结果 拓扑图 采用如下的思路配置小型网络的WLAN基本业务&#xff1a;1.配置AP、AC、…
阅读更多...
百度Apollo新版本Beta技术沙龙参会体验

百度Apollo新版本Beta技术沙龙参会体验

在自动驾驶领域&#xff0c;百度的Apollo一直是业界开源的标杆。其持续升级和创新的开源项目为整个自动驾驶行业树立了典范&#xff0c;不仅推动了技术的发展&#xff0c;也为广大的社区开发者们提供了学习和参考的范本。最近百度发布了Apollo新的Beta版本&#xff0c; 新版本B…
阅读更多...
代码随想录算法训练营 ---第五十六天

代码随想录算法训练营 ---第五十六天

今天同样是 动态规划&#xff1a;编辑距离问题&#xff01; 第一题&#xff1a; 简介&#xff1a; 本题有两个思路&#xff1a; 1.求出最长公共子串&#xff0c;然后返还 word1.length()word2.length()-2*dp[word1.size()][word2.size()] 本思路解法与求最长公共子串相同&…
阅读更多...
财报解读：立足海外音视频直播战场，欢聚的BIGO盾牌还需加强？

财报解读：立足海外音视频直播战场，欢聚的BIGO盾牌还需加强？

如今&#xff0c;音视频社交平台出海早已不是新鲜事&#xff0c;随着时间推移&#xff0c;一批“坚定全球化不动摇”的企业也实现突围&#xff0c;站在出海舞台中心。 若提到中国企业出海范本&#xff0c;欢聚集团定是绕不开的存在。作为最早一批出海的中国互联网企业&#xf…
阅读更多...
服务器数据恢复—重装系统导致XFS文件系统分区丢失的数据恢复案例

服务器数据恢复—重装系统导致XFS文件系统分区丢失的数据恢复案例

服务器数据恢复环境&#xff1a; 服务器使用磁盘柜RAID卡搭建了一组riad5磁盘阵列。服务器上层分配了一个LUN&#xff0c;划分了两个分区&#xff1a;sdc1分区和sdc2分区。通过LVM扩容的方式&#xff0c;将sdc1分区加入到了root_lv中&#xff1b;sdc2分区格式化为XFS文件系统。…
阅读更多...
github使用方法【附安装包】

github使用方法【附安装包】

如果你是一枚Coder&#xff0c;但是你不知道Github&#xff0c;那么我觉的你就不是一个菜鸟级别的Coder&#xff0c;因为你压根不是真正Coder&#xff0c;你只是一个Code搬运工。说明你根本不善于突破自己&#xff01;为什么这么说原因很简单&#xff0c;很多优秀的代码以及各种…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023