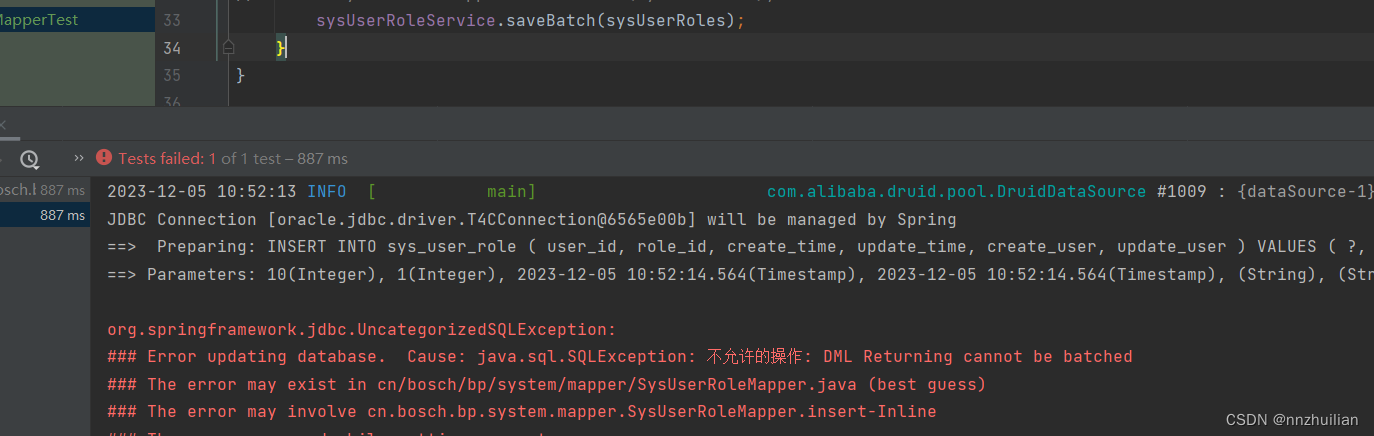
本文仅供学习使用
本文参考：
B站：DR_CAN

---

1. 线性系统 Linear System 与 叠加原理 Superposition

$$\dot{x}=f\left(x\right)$$

1. $x_1,x_2$ 是解
2. $x_3=k_1{x}_1+k_2{x}_2,k_1,k_2\in \mathbb{R}$
3. $x_3$ 是解

eg:
$$\begin{gathered} \ddot{x}+2\dot{x}+\sqrt{2}x=0\surd \\ \ddot{x}+2\dot{x}+\sqrt{2}{x}^2=0\times \\ \ddot{x}+\sin \dot{x}+\sqrt{2}x=0\times \end{gathered}$$

2. 线性化：Taylor Series

$$f\left(x\right)=f\left(x_0\right)+\frac{f^{\prime }\left(x_0\right)}{1!}\left(x-x_0\right)+\frac{{f^{\prime }}^{\prime }\left(x_0\right)}{2!}{\left(x-x_0\right)}^2+\cdots +\frac{f^n\left(x_0\right)}{n!}{\left(x-x_0\right)}^n$$

若$x-x_0\to 0,{\left(x-x_0\right)}^n\to 0$，则有：$\Rightarrow f\left(x\right)=f\left(x_0\right)+f^{\prime }\left(x_0\right)\left(x-x_0\right)\Rightarrow f\left(x\right)=k_1+k_{2}x-k_3{x}_0\Rightarrow f\left(x\right)=k_{2}x+b$

eg1:

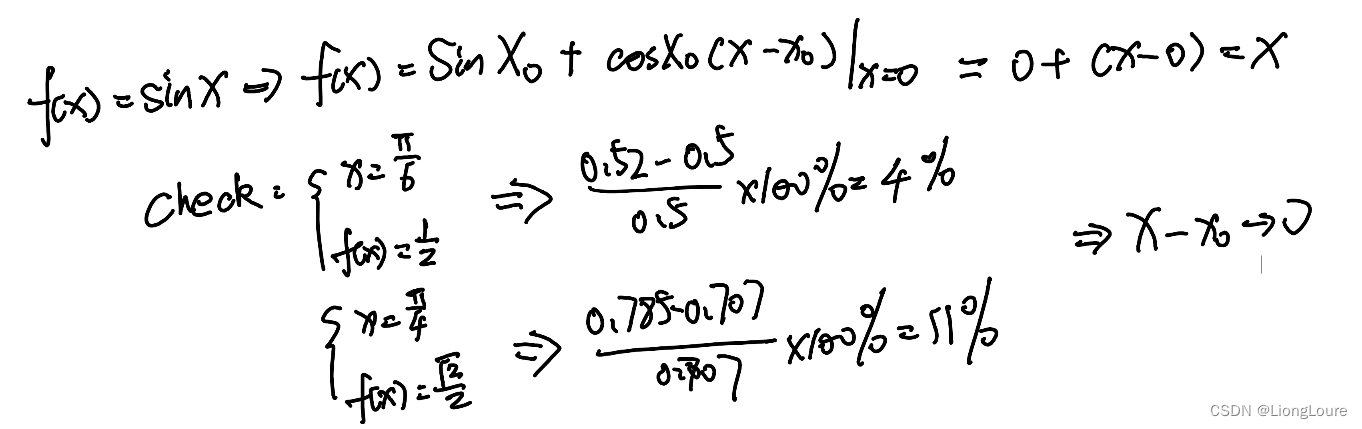
eg2:

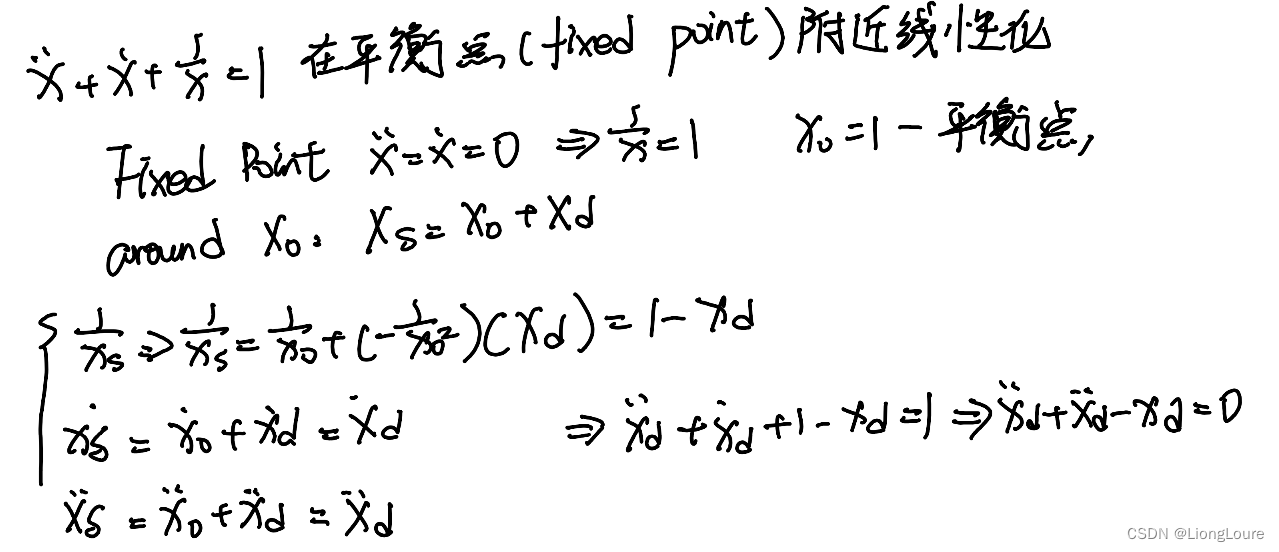
eg3:

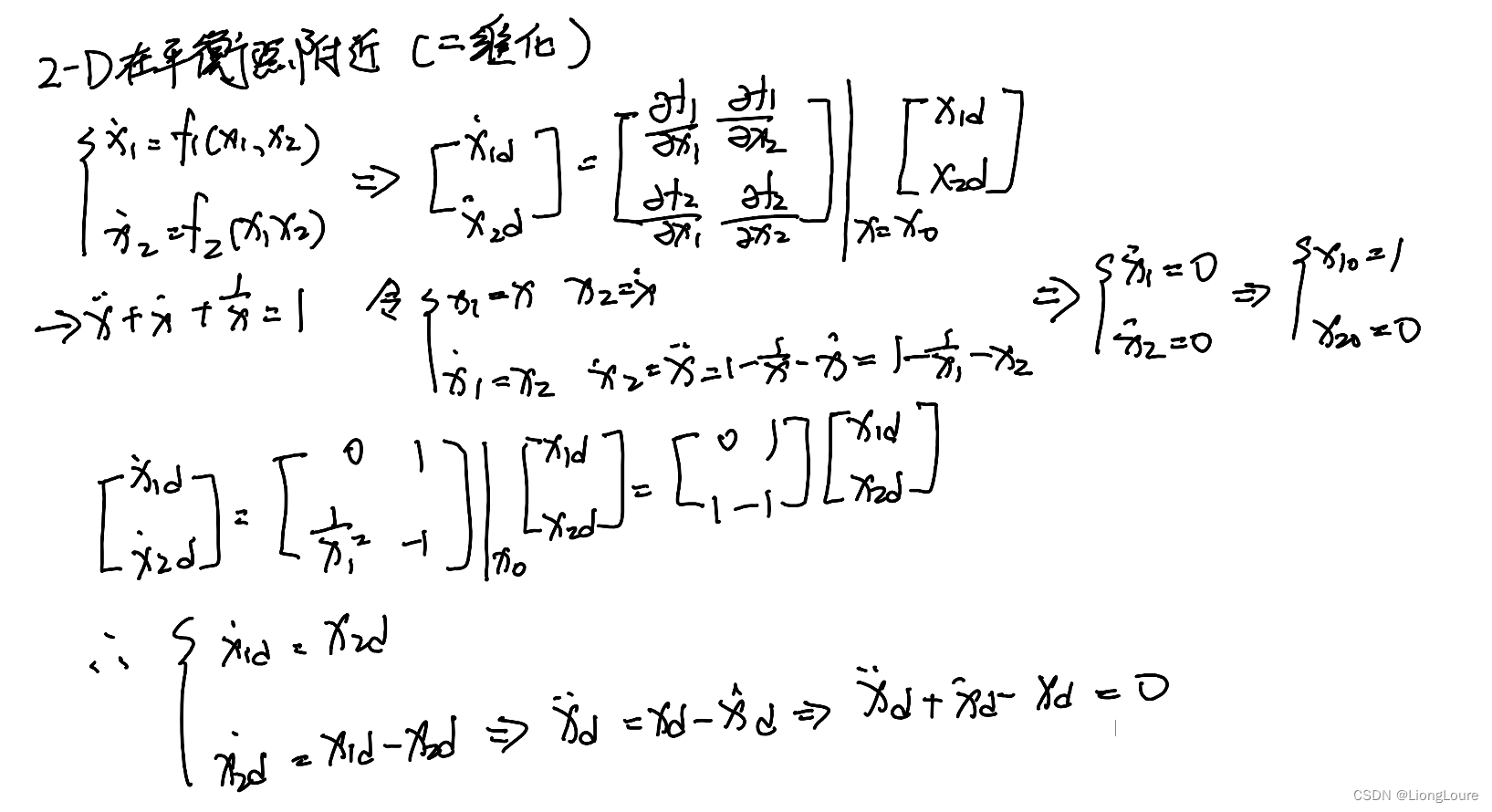
3. Summary

1. $f\left(x\right)=f\left(x_0\right)+\frac{f^{\prime }\left(x_0\right)}{1!}\left(x-x_0\right),x-x_0\to 0$
2. $\left[\begin{array}{c}{\dot{x}}_{1\mathrm{d}}\\ {\dot{x}}_{2\mathrm{d}}\end{array}\right]={\left[\begin{array}{cc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}\end{array}\right]|}_{\mathrm{x}={\mathrm{x}}_0}\left[\begin{array}{c}{x}_{1\mathrm{d}}\\ x_{2\mathrm{d}}\end{array}\right]$