使用肘部法则选择KMeans聚类中的k值

news2024/11/27 10:44:10

在这篇文章中，我们将讨论如何选择最好的k（聚类数）的k-Means聚类算法。

肘部法则简介

任何无监督算法的基本步骤是确定数据可以被聚类到的聚类的最佳数量。因为我们在无监督学习中没有任何预定义数量的聚类。我们倾向于使用一些可以帮助我们决定最佳聚类数的方法。在K-Means聚类的情况下，我们使用肘部法则来定义最佳的聚类数。

什么是K-Means聚类中肘部法则？

如我们所知，在k-means聚类算法中，我们随机初始化k个聚类，并且我们迭代地调整这k个聚类，直到这些k-质心处于平衡状态。然而，在初始化这些集群之前，我们要做的主要事情是确定我们必须使用多少个集群。

对于确定K（簇的数目），我们使用肘部法则。肘部法则是一种用于确定在k均值聚类算法中使用的质心数（k）的技术。在这种方法中，为了确定k值，我们连续迭代k=1到k=n（这里n是我们根据要求选择的超参数）。对于k的每个值，我们计算簇内平方和（WCSS）值。

WCSS -每个样本到簇内中心点的距离偏差之和。

现在，为了确定最佳的聚类数（k），我们绘制了k与它们的WCSS值的关系图。令人惊讶的是，该图看起来像一个肘部（我们将在后面看到）。此外，当k=1时，WCSS具有最高值，但随着k值的增加，WCSS值开始减小。我们从图开始看起来像直线的地方选择k值。

使用Sklearn实现

我们将看到如何在4个步骤中实现肘部法则。首先，我们将创建随机数据集点，然后我们将在此数据集上应用k均值，并计算1到4之间的k的wcss值。

步骤1：导入所需的库

from sklearn.cluster import KMeans
from sklearn import metrics
from scipy.spatial.distance import cdist
import numpy as np
import matplotlib.pyplot as plt

步骤2：创建和可视化数据

我们将创建一个随机数组并将其分布可视化

# Creating the data
x1 = np.array([3, 1, 1, 2, 1, 6, 6, 6, 5, 6,\
               7, 8, 9, 8, 9, 9, 8, 4, 4, 5, 4])
x2 = np.array([5, 4, 5, 6, 5, 8, 6, 7, 6, 7, \
               1, 2, 1, 2, 3, 2, 3, 9, 10, 9, 10])
X = np.array(list(zip(x1, x2))).reshape(len(x1), 2)
 
# Visualizing the data
plt.plot()
plt.xlim([0, 10])
plt.ylim([0, 10])
plt.title('Dataset')
plt.scatter(x1, x2)
plt.show()

输出
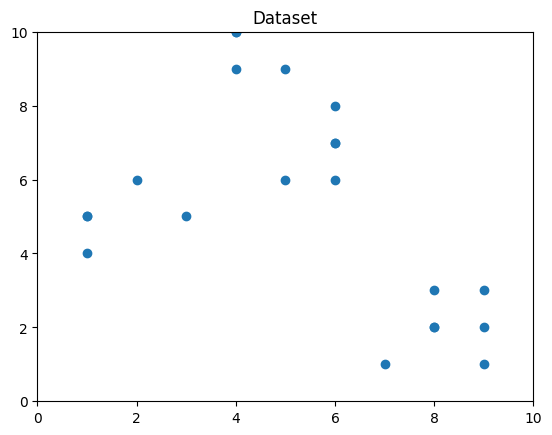
在这里插入图片描述
从上面的可视化中，我们可以看到集群的最佳数量应该在3左右。但是，仅仅可视化数据并不能总是给予正确的答案。

            Distortion = 1/n * Σ(distance(point, centroid)^2)

定义一个Distortion，通常，使用欧几里得距离度量。

Inertia：它是样本到其最近聚类中心的平方距离之和。

             Inertia = Σ(distance(point, centroid)^2)

我们将k的值从1迭代到n，并计算每个k值的Distortion，给定范围内每个k值的Inertia。

步骤3：构建聚类模型并计算Distortion和Inertia的值

distortions = []
inertias = []
mapping1 = {}
mapping2 = {}
K = range(1, 10)

for k in K:
	# Building and fitting the model
	kmeanModel = KMeans(n_clusters=k).fit(X)
	kmeanModel.fit(X)

	distortions.append(sum(np.min(cdist(X, kmeanModel.cluster_centers_,
										'euclidean'), axis=1)) / X.shape[0])
	inertias.append(kmeanModel.inertia_)

	mapping1[k] = sum(np.min(cdist(X, kmeanModel.cluster_centers_,
								'euclidean'), axis=1)) / X.shape[0]
	mapping2[k] = kmeanModel.inertia_

步骤4：列表和可视化结果

a）使用不同的Distortion值：

for key, val in mapping1.items():
	print(f'{key} : {val}')

输出

1 : 3.625551331197001
2 : 2.0318238533112596
3 : 1.2423303391744152
4 : 0.8367738708386461
5 : 0.736979754424859
6 : 0.6898254810112422
7 : 0.6020311621770951
8 : 0.5234596363982826
9 : 0.4587221418509788

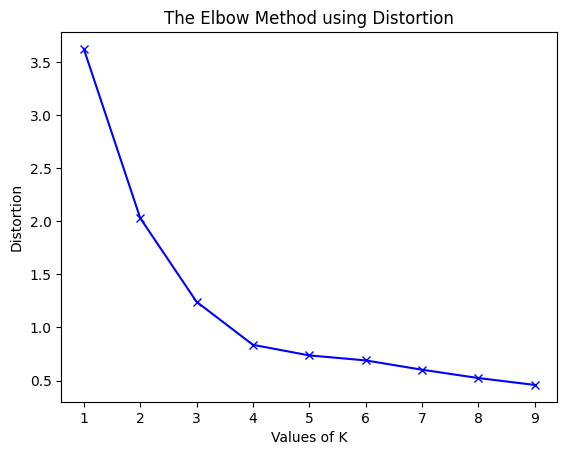
接下来我们将绘制k与WCSS的关系图

plt.plot(K, distortions, 'bx-')
plt.xlabel('Values of K')
plt.ylabel('Distortion')
plt.title('The Elbow Method using Distortion')
plt.show()

在这里插入图片描述
b）使用不同的Inertia：

for key, val in mapping2.items():
    print(f'{key} : {val}')

输出

1 : 312.95238095238096
2 : 108.07142857142856
3 : 39.51746031746031
4 : 17.978571428571428
5 : 14.445238095238096
6 : 11.416666666666668
7 : 9.266666666666667
8 : 7.25
9 : 6.5

plt.plot(K, inertias, 'bx-')
plt.xlabel('Values of K')
plt.ylabel('Inertia')
plt.title('The Elbow Method using Inertia')
plt.show()

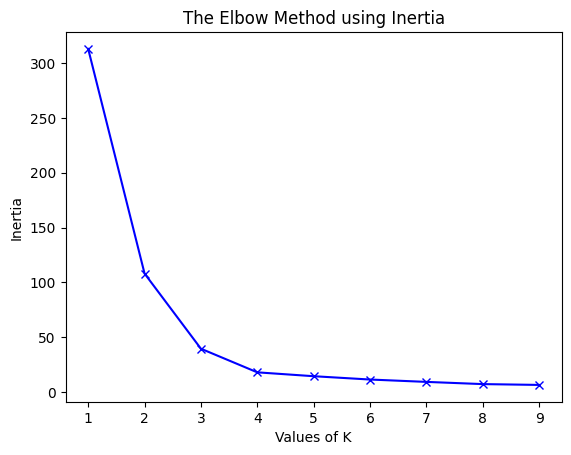
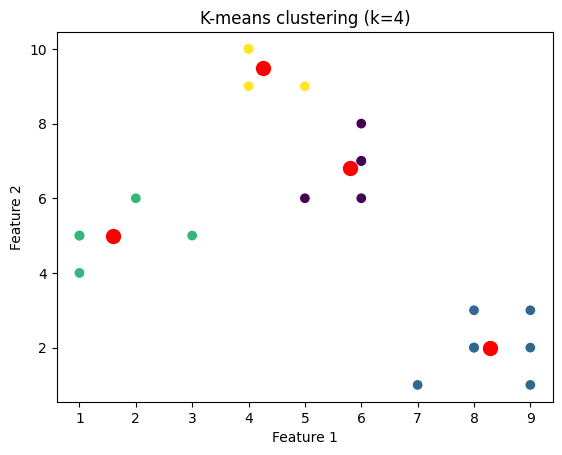
在这里插入图片描述
为了确定聚类的最佳数量，我们必须选择“弯头”处的k值，即distortion/inertia开始以线性方式减小的点。因此，对于给定的数据，我们得出结论，数据的最佳聚类数是4。

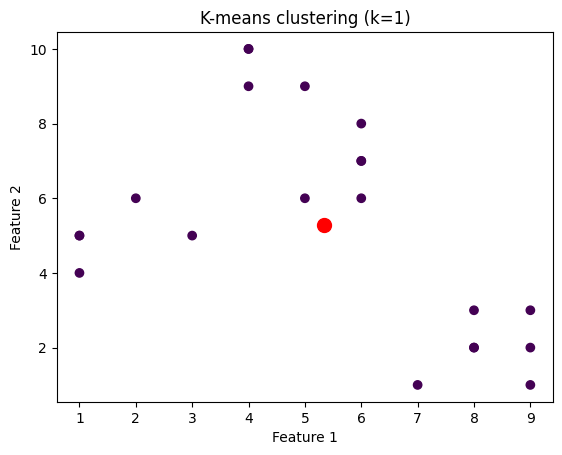
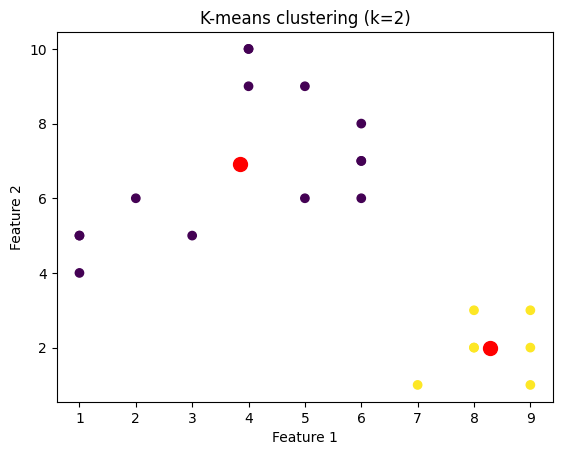
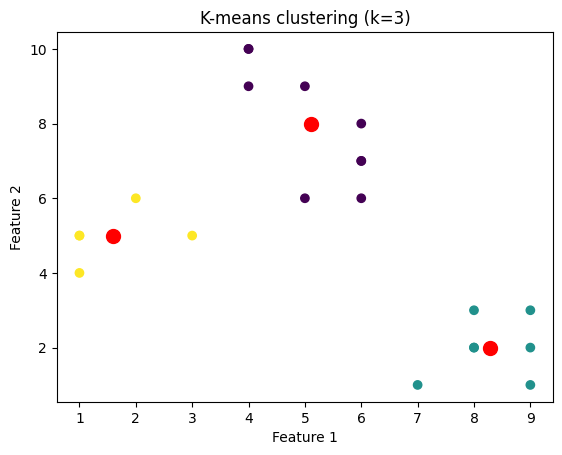
不同k值的聚类数据点

我们将绘制针对不同k值聚类的数据点的图像。为此，我们将通过迭代k值的范围来对数据集应用k-means算法。

import matplotlib.pyplot as plt

# Create a range of values for k
k_range = range(1, 5)

# Initialize an empty list to
# store the inertia values for each k
inertia_values = []

# Fit and plot the data for each k value
for k in k_range:
	kmeans = KMeans(n_clusters=k, \
					init='k-means++', random_state=42)
	y_kmeans = kmeans.fit_predict(X)
	inertia_values.append(kmeans.inertia_)
	plt.scatter(X[:, 0], X[:, 1], c=y_kmeans)
	plt.scatter(kmeans.cluster_centers_[:, 0],\
				kmeans.cluster_centers_[:, 1], \
				s=100, c='red')
	plt.title('K-means clustering (k={})'.format(k))
	plt.xlabel('Feature 1')
	plt.ylabel('Feature 2')
	plt.show()

# Plot the inertia values for each k
plt.plot(k_range, inertia_values, 'bo-')
plt.title('Elbow Method')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Inertia')
plt.show()