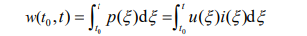【读点论文】A Survey of Quantization Methods for Efficient Neural Network Inference

A Survey of Quantization Methods for Efficient Neural Network Inference

Abstract

一旦抽象的数学计算适应了数字计算机的计算，在这些计算中如何有效地表示、处理和传递数值的问题就出现了。与数字表示问题密切相关的是量化问题:一组连续的实值数应该以何种方式分布在一组固定的离散数字上，以最小化所需的位数，并最大化随之而来的计算的准确性?每当内存和/或计算资源受到严重限制时，这个长期存在的量化问题就显得尤为重要。近年来，由于神经网络模型在计算机视觉、自然语言处理和相关领域的卓越表现，量化问题已经成为人们关注的焦点。从浮点表示转换为用4位或更少表示的低精度固定整数值，有可能将内存占用和延迟减少16倍;实际上，在这些应用程序中，通常可以实现4到8倍的减少。因此，毫不奇怪，量化最近已经成为一个重要的和非常活跃的研究子领域，有效地实现与神经网络相关的计算。在本文中，我们综述了深度神经网络计算中量化数值问题的方法，涵盖了当前方法的优点/缺点。通过这项调查及其组织，我们希望对当前神经网络量化研究提供一个有用的快照，并给出一个智能的组织来简化对该领域未来研究的评估。
大型语言模型（LLM）在各种任务中表现出色。然而，即便有卓越的任务处理能力，LLM 却面临着巨大的挑战，这些挑战源于其巨大的规模和计算需求。举个例子，GPT-175B 版本具有惊人的 1750 亿参数，至少需要 320GB（使用 1024 的倍数）的半精度（FP16）格式存储。此外，部署此模型进行推理还需要至少五个 A100 GPU，每个 GPU 具有 80GB 的内存，这样才能有效地保证运行。为了解决这些问题，当下一种被称为模型压缩的方法可以成为解决方案。模型压缩可以将大型、资源密集型模型转换为适合存储在受限移动设备上的紧凑版本。此外它可以优化模型，以最小的延迟更快地执行，或实现这些目标之间的平衡。一定程度上，网络越深，参数越多，模型也会越复杂，但其最终效果也越好，而模型压缩算法是旨在将一个庞大而复杂的预训练模型转化为一个精简的小模型。深度学习模型压缩方法综述 - 知乎 (zhihu.com)
因为嵌入式设备的算力和内存有限，因此深度学习模型需要经过模型压缩后，方才能部署到嵌入式设备上。模型压缩问题的定义可以从 3 角度出发:
- 模型压缩的收益:计算: 减少浮点运算量（FLOPs），降低延迟（Latency）；存储: 减少内存占用，提高 GPU/NPU 计算利用率
- 模型压缩问题的约束
- 公式定义模型压缩问题
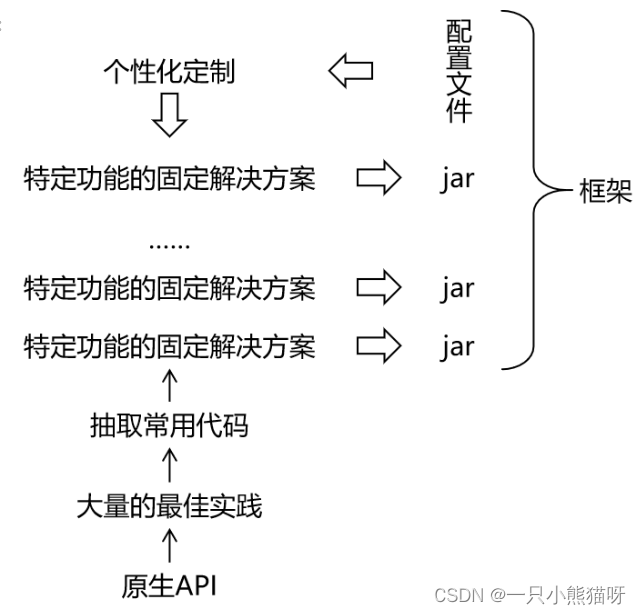
按照压缩过程对网络结构的破坏程度，《解析卷积神经网络》一书中将模型压缩技术分为“前端压缩”和“后端压缩”两部分:
- 前端压缩，是指在不改变原网络结构的压缩技术，主要包括知识蒸馏、轻量级网络（紧凑的模型结构设计）以及滤波器（filter）层面的剪枝（结构化剪枝）等；
- 后端压缩，是指包括低秩近似、未加限制的剪枝（非结构化剪枝/稀疏）、参数量化以及二值网络等，目标在于尽可能减少模型大小，会对原始网络结构造成极大程度的改造。
总结：前端压缩几乎不改变原有网络结构（仅仅只是在原模型基础上减少了网络的层数或者滤波器个数），后端压缩对网络结构有不可逆的大幅度改变，造成原有深度学习库、甚至硬件设备不兼容改变之后的网络。其维护成本很高。

INTRODUCTION

在过去的十年中，我们已经观察到神经网络(nn)在广泛问题上的准确性有了显著的提高，通常是通过高度过度参数化的模型实现的。虽然这些过度参数化(因此非常大)的神经网络模型的准确性显著提高，但这些模型的绝对规模意味着不可能将它们部署到许多资源受限的应用程序中。这给实现普适深度学习带来了一个问题，因为普适深度学习需要在资源受限的环境下，以低能耗和高精度进行实时推理。这种无处不在的深度学习预计将对实时智能医疗监控、自动驾驶、音频分析和语音识别等广泛应用产生重大影响。
要实现具有最佳精度的高效实时神经网络，需要重新思考神经网络模型的设计、训练和部署[71]。有大量的文献专注于通过使NN模型更有效(在延迟、内存占用和能耗等方面)来解决这些问题，同时仍然提供最佳的准确性/泛化权衡。这些努力大致可分为以下几类。
- a)设计高效的神经网络模型架构:一条工作线侧重于在微架构(例如，内核类型，如深度卷积或低秩分解)以及宏观架构(例如，模块类型，如残差或初始化)方面优化NN模型架构。这里的经典技术主要是使用手动搜索来找到新的架构模块，这是不可扩展的。因此，新的工作方向是设计自动机器学习(AutoML)和神经结构搜索(NAS)方法。这些目标是在给定模型大小、深度和/或宽度的约束下，以自动化的方式找到正确的神经网络架构。
- b)协同设计神经网络架构和硬件:最近的另一项工作是为特定的目标硬件平台调整(和共同设计)神经网络架构。这一点很重要，因为神经网络组件的开销(在延迟和能量方面)依赖于硬件。例如，具有专用缓存层次结构的硬件可以比没有这种缓存层次结构的硬件更有效地执行带宽限制的操作。与神经网络架构设计类似，架构-硬件协同设计的初始方法是手动的，其中专家将适应/更改神经网络架构，然后使用自动化的AutoML和/或NAS技术。
- c)修剪:另一种减少神经网络内存占用和计算成本的方法是应用剪枝。在剪枝过程中，去除小显著性(敏感性)的神经元，得到稀疏计算图。这里，具有小显著性的神经元是那些被移除对模型输出/损失函数影响最小的神经元。修剪方法大致可分为非结构化修剪和结构化修剪。通过非结构化修剪，人们可以去除具有小显著性的神经元，无论它们出现在哪里。使用这种方法，可以执行主动修剪，去除大多数神经网络参数，对模型的泛化性能影响很小。然而，这种方法会导致稀疏矩阵运算，这种运算很难加速，而且通常是内存受限的。另一方面，使用结构化修剪，一组参数(例如，整个卷积滤波器)被删除。这具有改变层和权重矩阵的输入和输出形状的效果，因此仍然允许密集矩阵操作。然而，积极的结构化修剪往往导致显著的精度下降。具有高水平修剪/稀疏性的训练和推理，同时保持最先进的性能，仍然是一个悬而未决的问题。建议有兴趣的读者参阅[The state of sparsity in deep neural networks,Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks,Taxonomy and evaluation of structured compression of convolutional neural networks]，以了解修剪/稀疏性相关工作的全面调查。
- d)知识提炼:模型蒸馏涉及到训练一个大型模型，然后用它作为老师来训练一个更紧凑的模型。在学生模型的训练过程中，模型蒸馏的关键思想不是使用“硬”类标签，而是利用老师产生的“软”概率，因为这些概率可以包含更多关于输入的信息。尽管在蒸馏方面做了大量的工作，但这里的一个主要挑战是仅通过蒸馏实现高压缩比。与量化和剪枝在≥4倍压缩(INT8和较低精度)时仍能保持性能相比，知识蒸馏方法在严重压缩时往往会出现不可忽略的精度下降。然而，将知识蒸馏与先前的方法(即量化和修剪)相结合已经取得了巨大的成功。
- e)量化:最后，量化是一种在神经网络模型的训练和推理中都表现出巨大和一致成功的方法。虽然数字表示和量化问题与数字计算一样古老，但神经网络提供了独特的改进机会。虽然对量化的调查主要集中在推理上，但我们应该强调，量化在神经网络训练方面取得了重要的成功。特别是，半精度和混合精度训练的突破已经成为使AI加速器的吞吐量提高数量级的主要驱动因素。然而，事实证明，在不进行重大调整的情况下很难达到半精度以下，而且最近的大多数量化研究都集中在推理上。这种用于推理的量化是本文的重点。
- f) Quantization and Neuroscience:神经科学中与神经网络量化松散相关的研究表明，人脑以离散/量化形式存储信息，而不是以连续形式存储信息。这一观点的一个流行理由是，以连续形式存储的信息将不可避免地受到噪声的破坏(噪声总是存在于物理环境中，包括我们的大脑，并且可以由热噪声、感觉噪声、外部噪声、突触噪声等引起)。然而，离散信号表示对这种低水平噪声具有更强的鲁棒性。也有人提出了其他原因，包括离散表示具有更高的泛化能力，以及在有限资源下具有更高的效率。
- 这项工作的目标是介绍目前在量化中使用的方法和概念，并讨论当前在这一研究领域的挑战和机遇。在这样做的过程中，我们试图讨论最相关的工作。在篇幅有限的简短调查中，不可能讨论像神经网络量化这样大领域的每一项工作;毫无疑问，我们遗漏了一些相关的论文。我们提前向我们可能忽略的论文的读者和作者道歉。
工业界主流的模型压缩方法有：知识蒸馏（Knowledge Distillation，KD）轻量化模型架构（也叫紧凑的模型设计）、剪枝（Pruning）、量化（Quantization）。各个模型压缩方法总结如下：
- 知识蒸馏：属于迁移学习的一种，主要思想是将学习能力强的复杂教师模型中的“知识”迁移到简单的学生模型中。经典KD论文，属于蒸 "logits"方法，将Teacher Network输出的soft label作为标签来训练Student Network。必须重新训练模型。针对卷积和全连接层
- 剪枝：将权重低于阈值的连接都从网络中删除。剪枝步骤：正常训练，删除网络中权重低于阈值的连接层，重新训练。需要重新训练模型。
- 量化：指将神经网络的浮点算法转换为定点算法，TensoRT框架中的基于 KL 散度方法的INT8量化策略是主流技术。PTQ 训练后量化方法不需要重新训练模型。对卷积、全连接、激活、BN层等会有影响
一个复杂模型可由多个简单模型或者强约束条件训练得到。复杂模型特点是性能好，但其参数量大，计算效率低。小模型特点是计算效率高，但是其性能较差。知识蒸馏是让小模型去拟合大模型，从而让小模型学到与大模型相似的函数映射。使其保持其快速的计算速度前提下，同时拥有复杂模型的性能，达到模型压缩的目的。模型蒸馏的关键在于监督特征的设计，例如使用 Soft Target（软标签KD）所提供的类间相似性作为依据，或使用大模型的中间层特征图或 attention map作为暗示，对小网络进行训练。
深度学习模型中一般存在着大量冗余的参数，将权重矩阵中相对“不重要”的权值剔除（即置为 0），可达到降低计算资源消耗和提高实时性的效果，而对应的技术则被称为模型剪枝。剪枝算法步骤：
- 正常训练模型；模型剪枝；重新训练模型。以上三个步骤反复迭代进行，直到模型精度达到目标，则停止训练。
模型剪枝算法根据粒度的不同，可以粗分为4种粒度：细粒度剪枝(fine-grained)：对连接或者神经元进行剪枝，它是粒度最小的剪枝。向量剪枝(vector-level)：它相对于细粒度剪枝粒度更大，属于对卷积核内部(intra-kernel)的剪枝。核剪枝(kernel-level)：去除某个卷积核，它将丢弃对输入通道中对应计算通道的响应。滤波器剪枝(Filter-level)：对整个卷积核组进行剪枝，会造成推理过程中输出特征通道数的改变。
模型量化是指将神经网络的浮点算法转换为定点。量化有一些相似的术语，低精度（Low precision）可能是常见的。低精度模型表示模型权重数值格式为 FP16（半精度浮点）或者 INT8（8位的定点整数），但是目前低精度往往就指代 INT8。常规精度模型则一般表示模型权重数值格式为 FP32（32位浮点，单精度）。混合精度（Mixed precision）则在模型中同时使用 FP32 和 FP16 的权重数值格式。 FP16 减少了一半的内存大小，但有些参数或操作符必须采用 FP32 格式才能保持准确度。模型量化过程可以分为两部分：将模型从 FP32 转换为 INT8（即量化算术过程），以及使用 INT8 进行推理。在实践中将浮点模型转为量化模型的方法有以下三种方法：
- data free：不使用校准集，传统的方法直接将浮点参数转化成量化数，使用上非常简单，但是一般会带来很大的精度损失，但是高通最新的论文 DFQ 不使用校准集也得到了很高的精度。
- calibration：基于校准集方案，通过输入少量真实数据进行统计分析。很多芯片厂商都提供这样的功能，如 tensorRT、高通、海思、地平线、寒武纪
- finetune：基于训练 finetune 的方案，将量化误差在训练时仿真建模，调整权重使其更适合量化。好处是能带来更大的精度提升，缺点是要修改模型训练代码，开发周期较长。
按照量化阶段的不同，量化方法分为以下两种：Post-training quantization PTQ（训练后量化、离线量化）；Quantization-aware training QAT（训练时量化，伪量化，在线量化）。
目前已知的加快推理速度概率较大的量化方法主要有：二值化，其可以用简单的位运算来同时计算大量的数。对比从 nvdia gpu 到 x86 平台，1bit 计算分别有 5 到128倍的理论性能提升。且其只会引入一个额外的量化操作，该操作可以享受到 SIMD（单指令多数据流）的加速收益。线性量化(最常见)，又可细分为非对称，对称和 ristretto 几种。在 nvdia gpu，x86、arm 和部分 AI 芯片平台上，均支持 8bit 的计算，效率提升从 1 倍到 16 倍不等，其中 tensor core 甚至支持 4bit计算，这也是非常有潜力的方向。线性量化引入的额外量化/反量化计算都是标准的向量操作，因此也可以使用 SIMD 进行加速，带来的额外计算耗时不大。对数量化，一种比较特殊的量化方法。两个同底的幂指数进行相乘，那么等价于其指数相加，降低了计算强度。同时加法也被转变为索引计算。目前 nvdia gpu，x86、arm 三大平台上没有实现对数量化的加速库，但是目前已知海思 351X 系列芯片上使用了对数量化。

GENERAL HISTORY OF QUANTIZATION

Gray和Neuhoff对1998年之前的量化历史写了一篇很好的综述。这篇文章写得很好，值得一读;然而，为了读者的方便，我们将在这里简要总结一些关键点。量化作为一种将大(通常是连续的)集合中的输入值映射到小(通常是有限的)集合中的输出值的方法，有着悠久的历史。舍入和截断是典型的例子。量化与微积分的基础有关，相关的方法可以在19世纪早期(以及更早)看到，例如，在最小二乘的早期工作和大规模(按19世纪早期的标准)数据分析的相关技术。量化的早期工作可以追溯到1867年，其中离散化被用来近似积分的计算;随后，在1897年，Shappard研究了舍入误差对积分结果的影响。最近，量化在数字信号处理中很重要，因为以数字形式表示信号的过程通常涉及四舍五入，以及在数值分析和数值算法的实现中，对实数的计算是用有限精度算法实现的。
直到1948年，在数字计算机出现前后，香农撰写了关于通信数学理论的开创性论文，量化的影响及其在编码理论中的应用才被正式提出。特别是，香农在他的无损编码理论中认为，当感兴趣的事件具有非均匀概率时，使用相同数量的比特是浪费的。他认为，更理想的方法是根据事件发生的概率来改变比特数，这个概念现在被称为可变速率量化。霍夫曼编码尤其受此影响。在1959年的后续工作中，香农引入了失真率函数(它提供了编码后信号失真的下界)以及矢量量化的概念(也在第IV-F节中简要讨论)。这个概念在之后的工作中得到了扩展，并在实际通信应用中变得实用。那段时期关于信号处理中量化的其他重要历史研究包括，该研究引入了脉冲编码调制(PCM)概念(一种用于近似/表示/编码采样模拟信号的脉冲方法)，以及高分辨率量化的经典结果。
量化以一种稍微不同的方式出现在算法中，它使用数值近似来解决涉及连续数学量的问题，这一领域也有很长的历史，但随着数字计算机的出现，它也重新引起了人们的兴趣。在数值分析中，一个重要的概念曾经是(现在仍然是)适定问题——粗略地说，一个问题是适定的，如果:一个解存在;这个解决方案是独一无二的;这个解持续依赖于输入数据在一些合理的拓扑结构中。这类问题有时被称为条件良好的问题。事实证明，即使在处理给定的条件良好的问题时，在某种理想意义上“准确”解决该问题的某些算法，在存在由舍入和截断误差的特性引入的“噪声”时，也会表现得非常糟糕。这些舍入误差与用有限位表示实数有关，这是由IEEE浮点标准规定的量化;由于迭代算法实际上只能执行有限次数的迭代，因此会出现截断误差。后者甚至在“精确算术”中也很重要，因为连续数学的大多数问题甚至在原则上都不能用有限的初等运算序列来解决;但前者与量子化有关。这些问题引出了算法数值稳定性的概念。让我们把数值算法看作一个函数f，它试图将输入数据x映射到“真实”解y;但是由于舍入和截断误差，该算法的输出实际上是另一个y *。在这种情况下，算法的前向误差为∆y = y∗−y;算法的后向误差最小∆x使f(x +∆x) = y∗。因此，前向误差告诉我们准确或真实答案与算法输出之间的差异;反向误差告诉我们，我们运行的算法实际上准确地解决了哪些输入数据。算法的前向误差和后向误差与问题的条件数有关。

A. Quantization in Neural Nets

毫无疑问，已经有成千上万的论文写在这些主题上，人们可能会想:最近关于神经网络量化的工作与这些早期的工作有什么不同?当然，最近提出的许多“新算法”与过去文献中的工作有很强的联系(在某些情况下本质上是对过去工作的重新发现)。然而，神经网络给量化问题带来了独特的挑战和机遇。首先，神经网络的推理和训练都是计算密集型的。因此，数值的有效表示就显得尤为重要。其次，大多数当前的神经网络模型都严重过度参数化，因此有足够的机会在不影响精度的情况下降低比特精度。然而，一个非常重要的区别是，神经网络对激进量化和极端离散化非常鲁棒。这里的新自由度与所涉及的参数数量有关，也就是说，我们正在处理过度参数化的模型。这直接影响到我们是在解决适定问题，是对前向误差还是后向误差感兴趣，等等。在推动量化最新发展的神经网络应用中，没有一个单一的适定或适条件问题正在得到解决。相反，人们对某种前向误差度量(基于分类质量、困惑度等)感兴趣，但由于过度参数化，有许多非常不同的模型可以精确或近似地优化该度量。因此，在量化模型与原始非量化模型之间具有较高的误差/距离的同时，仍然可以获得非常好的泛化性能。这种增加的自由度在许多经典研究中并不存在，这些研究主要集中在寻找不会过多改变信号的压缩方法，或者使用数值方法，其中对“精确”与“离散”计算之间的差异有很强的控制。这一观察结果一直是研究神经网络量化新技术的主要驱动力。最后，神经网络模型的分层结构提供了一个额外的维度来探索。神经网络中不同的层对损失函数有不同的影响，这激发了混合精度量化方法。

III. BASIC CONCEPTS OF QUANTIZATION

A. Problem Setup and Notations

假设NN有L层具有可学习参数，记为{W1, W2，…， WL}，其中θ表示所有这些参数的组合。在不损失一般性的情况下，我们专注于监督学习问题，其名义目标是优化以下经验风险最小化函数:
- $L(\theta)\frac{1}{N}\sum_{i=1}^Nl(x_i,y_i;\theta)$
- 式中(x, y)为输入数据及对应的标号，l(x, y;θ)为损失函数(如均方误差或交叉熵损失)，N为数据点总数。我们也将第i层的输入隐藏激活表示为hi，对应的输出隐藏激活表示为ai。我们假设我们有训练好的模型参数θ，以浮点精度存储。在量化中，目标是将参数(θ)以及中间激活映射(即hi, ai)的精度降低到低精度，同时对模型的泛化能力/精度影响最小。为此，我们需要定义一个量化运算符，将浮点值映射到量化的浮点值，这将在下面描述。

B. Uniform Quantization

我们首先需要定义一个函数，它可以将神经网络的权重和激活量化到一个有限的值集。该函数接受浮点实值，并将它们映射到较低的精度范围，如下图所示。
- 均匀量化(左)与非均匀量化(右)的比较。连续域r中的实值映射到量子化域Q中离散的、精度较低的值，用橙色子弹标记。请注意，在均匀量化中，量子化值(量化水平)之间的距离是相同的，而在非均匀量化中，它们可以变化。
- 对称量化和非对称量化的说明。限制范围的对称量化将实值映射到[- 127,127]，对于8位量化，全范围映射到[- 128,127]。
量化函数的常用选择如下: $Q (r) = I n t (r / S) - Z$ 。其中Q为量化算子，r为实值输入(激活或权重)，S为实值缩放因子，Z为整数零点。此外，Int函数通过舍入操作(例如，舍入到最近和截断)将实值映射为整数值。本质上，这个函数是从实数r到某个整数值的映射。这种量化方法也被称为均匀量化，因为得到的量化值(又称量化级别)是均匀间隔的(上图，左)。还有一些非均匀量化方法，其量化值不一定是均匀间隔的(图1，右)，这些方法将在第III-F节中进行更详细的讨论。通过一种通常称为去量化的操作，可以从量子化的Q®中恢复实值r:
- $\bar{r}=S(Q(r)+Z)$
- 请注意，由于舍入操作，恢复的实值≈r将不完全匹配r。

C. Symmetric and Asymmetric Quantization

均匀量化的一个重要因素是上公式中比例因子S的选择。这个比例因子本质上是将给定的实数r范围划分为多个分区:
- $S=\frac{\beta-\alpha}{2^b-1}$
- 式中[α， β]表示裁剪范围，即对实值进行裁剪的有界范围，b为量化位宽度。因此，为了定义比例因子，首先要确定裁剪范围[α， β]。选择裁剪范围的过程通常称为校准。
一个简单的选择是使用信号的最小/最大值作为裁剪范围，即α = rmin， β = rmax。这种方法是一种非对称量化方案，因为裁剪范围不一定是相对于原点对称的，即 $\neq β$ ，如下图(右)所示。通过选择α =−β的对称裁剪范围，也可以使用对称量化方案。一个流行的选择是根据信号的最小/最大值来选择这些:−α = β = max(|rmax|， |rmin|)。与对称量化相比，非对称量化通常导致更窄的裁剪范围。当目标权重或激活不平衡时，这一点尤其重要，例如，ReLU之后的激活总是具有非负值。然而，使用对称量化，通过将零点替换为Z = 0，简化了Eq. 2中的量化函数:
- $Q(r)=Int(\frac{r}{S})$
- 这里，比例因子有两种选择。在“全量程”对称量化中，S被选择为$\frac{2max(|r|)}{2^n−1} $ (带舍入模式)，以使用[-128,127]的全INT8范围。然而，在“限制范围”中，S被选择为 $\frac{max(|r|)}{2^{n−1}−1}$ ，它只使用[-127,127]的范围。正如预期的那样，全范围方法更加准确。对称量化在量化权重的实践中被广泛采用，因为将零点归零可以减少推理过程中的计算成本，并且使实现更加简单。然而，请注意，对于激活，由于非对称激活中的偏移而占用的交叉项是一个静态的数据独立项，可以在偏置中吸收(或用于初始化累加器)。
利用信号的最小/最大值进行对称和非对称量化是一种常用的方法。然而，这种方法容易受到激活中的异常数据的影响。这些可能会不必要地增加范围，从而降低量化的分辨率。解决这个问题的一种方法是使用百分位数而不是信号的最小/最大值。也就是说，不是使用最大/最小值，而是使用第i个最大/最小值作为β/α。另一种方法是选择α和β，以最小化实值和量化值之间的KL散度(即信息损失)。
摘要(对称与非对称量化)。对称量化使用对称范围对裁剪进行分区。这样做的好处是更容易实现，因为它会导致Eq. 2中的Z = 0。然而，对于范围可能偏斜且不对称的情况，它是次优的。对于这种情况，不对称量化是首选。

D. Range Calibration Algorithms: Static vs Dynamic Quantization

到目前为止，我们讨论了确定[α， β]剪切范围的不同校准方法。量化方法的另一个重要区别是何时确定裁剪范围。这个范围可以静态地计算权重，因为在大多数情况下，在推理期间参数是固定的。然而，每个输入样本的激活映射是不同的(Eq. 1中的x)。因此，有两种量化激活的方法:动态量化和静态量化。
在动态量化中，此范围在运行时为每个激活映射动态计算。这种方法需要实时计算信号统计(最小、最大、百分位数等)，这可能会有非常高的开销。然而，动态量化通常会导致更高的精度，因为每个输入的信号范围都是精确计算的。
另一种量化方法是静态量化，其中裁剪范围是预先计算的，并且在推理期间是静态的。这种方法不会增加任何计算开销，但与动态量化相比，它通常会导致较低的精度。一种流行的预计算方法是运行一系列校准输入来计算典型的激活范围。已经提出了多个不同的度量来寻找最佳范围，包括最小化原始未量化权重分布与相应量化值之间的均方误差(MSE)。人们也可以考虑使用其他指标，如熵，尽管MSE是最常用的方法。另一种方法是在NN训练过程中学习/强加这个裁剪范围。这里值得注意的工作有LQNets、PACT、LSQ和LSQ+，它们在训练过程中共同优化了神经网络中的裁剪范围和权值。
摘要(动态与静态量化)。动态量化动态计算每个激活的裁剪范围，通常达到最高的精度。然而，动态计算信号的范围是非常昂贵的，因此，从业者通常使用静态量化，其中所有输入的裁剪范围是固定的。

E. Quantization Granularity

在大多数计算机视觉任务中，层的激活输入与许多不同的卷积过滤器进行卷积，如下图所示。每个卷积滤波器都可以有不同的取值范围。
- 不同量化粒度的说明。在分层量化中，对属于同一层的所有滤波器应用相同的裁剪范围。这可能导致具有窄分布的通道(例如图中的Filter 1)的不良量化分辨率。使用信道量化可以实现更好的量化分辨率，这种量化将不同的裁剪范围专用于不同的信道。
因此，量化方法的一个区别是如何为权重计算裁剪范围[α， β]的粒度。我们将它们分类如下。
- a)分层量化:该方法通过考虑一层卷积滤波器的所有权重来确定裁剪范围，如上图第三列所示。这里检查该层中整个参数的统计数据(例如，最小，最大，百分位数等)，然后对所有卷积滤波器使用相同的裁剪范围。虽然这种方法很容易实现，但由于每个卷积滤波器的范围可能变化很大，它通常会导致次优精度。例如，一个参数范围相对较窄的卷积核可能会因为同一层中另一个范围更大的核而失去其量化分辨率。
- b)分组量化:可以在一个层内分组多个不同的通道来计算裁剪范围(激活或卷积核)。这对于参数在单个卷积/激活中的分布变化很大的情况很有帮助。例如，这种方法在Q-BERT中被发现对由完全连接的注意层组成的Transformer模型进行量化很有用。然而，这种方法不可避免地带来了考虑不同缩放因子的额外成本。
- c)信道量化:一种常用的裁剪范围选择是对每个卷积滤波器使用固定值，独立于其他通道，如上图最后一列所示。也就是说，每个通道都分配了一个专用的缩放因子。这确保了更好的量化分辨率，并经常导致更高的精度。
- d)子通道量化:前面的方法可能会被采取到极端，其中裁剪范围是相对于卷积或全连接层中的任何一组参数确定的。然而，这种方法可能会增加相当大的开销，因为在处理单个卷积或全连接层时需要考虑不同的缩放因子。因此，分组量化可以在量化分辨率和计算开销之间建立一个很好的折衷方案。
摘要(量化粒度)。信道量化是目前用于卷积核量化的标准方法。它使实践者能够以微不足道的开销来调整每个内核的裁剪范围。相比之下，子通道量化可能会导致显著的开销，并且不是当前的标准选择。

F . Non-Uniform Quantization

文献中的一些工作也探索了非均匀量化，其中量化步骤和量化水平可以是非均匀间隔的。
- $Q(r) = X_i, if ~r ∈ [∆i, ∆i+1).$
- 具体来说，当实数r的值落在量化步长Δi和Δi+1之间时，量化器Q将其投影到相应的量化级别Xi。请注意，Xi 和 Δi 的间距都不是均匀的。
对于固定位宽，非均匀量化可以实现更高的精度，因为可以通过更多地关注重要值区域或找到适当的动态范围来更好地捕获分布。例如，许多非均匀量化方法是针对权重和激活的钟形分布而设计的，这些分布通常涉及长尾。典型的基于规则的非均匀量化是使用对数分布，其中量化步长和级别呈指数增长而不是线性增长。另一个流行的分支是基于二进制代码的量化，其中实数向量 r ∈ Rn 通过表示 $\sum^m_{i=1} α_ib_i$ 被量化为 m 个二进制向量，缩放因子为 αi ∈ R 和二元向量 bi ∈ {−1, +1}n。由于没有闭合形式的解决方案来最小化 r 和 $\sum^m_{i=1} α_ib_i$ 之间的误差，因此先前的研究依赖于启发式解决方案。为了进一步改进量化器，最近的工作将非均匀量化表述为优化问题。如方程式所示。调整量化器Q中的量化步长/级别以最小化原始张量和量化对应物之间的差异。
- $min_Q||Q(r)-r||^2$
- 此外，量化器本身也可以与模型参数联合训练。这些方法被称为可学习量化器，量化步骤/级别通常通过迭代优化或梯度下降进行训练。除了基于规则和基于优化的非均匀量化之外，聚类也有利于减轻量化造成的信息损失。一些工作在不同张量上使用 k 均值来确定量化步骤和级别，而其他工作在权重上应用 Hessian 加权 k 均值聚类以最小化性能损失。进一步的讨论可以在第 IV-F 节中找到。
摘要（均匀量化与非均匀量化）。一般来说，非均匀量化使我们能够通过非均匀地分配比特和离散化参数范围来更好地捕获信号信息。然而，非均匀量化方案通常难以在通用计算硬件（例如 GPU 和 CPU）上有效部署。因此，均匀量化由于其简单性和到硬件的高效映射而成为目前事实上的方法。

G. Fine-tuning Methods

量化后常常需要调整神经网络中的参数。这可以通过重新训练模型来执行，该过程称为量化感知训练 (QAT)，也可以在不重新训练的情况下完成，该过程通常称为训练后量化 (PTQ)。这两种方法之间的示意性比较如下图所示。
- 量化感知训练（QAT，左）和训练后量化（PTQ，右）之间的比较。在 QAT 中，对预训练模型进行量化，然后使用训练数据进行微调，以调整参数并恢复准确性下降。在 PTQ 中，使用校准数据（例如，训练数据的一个小子集）来校准预训练模型，以计算裁剪范围和缩放因子。然后，根据校准结果对模型进行量化。请注意，校准过程通常与 QAT 的微调过程并行进行。
量化感知训练：给定一个经过训练的模型，量化可能会对经过训练的模型参数引入扰动，这可能会使模型远离以浮点精度训练时收敛的点。可以通过使用量化参数重新训练神经网络模型来解决这个问题，以便模型可以收敛到具有更好损失的点。一种流行的方法是使用 QuantizationAware Training (QAT)，其中对浮点量化模型执行通常的前向和后向传递，但模型参数在每次梯度更新后进行量化（类似于投影梯度下降）。特别是，在以浮点精度执行权重更新之后进行此投影非常重要。使用浮点执行向后传递非常重要，因为以量化精度累积梯度可能会导致零梯度或具有高误差的梯度，尤其是在低精度情况下 。
反向传播中一个重要的微妙之处是如何处理不可微的量化算子。在没有任何近似的情况下，该算子的梯度几乎在任何地方都为零，因为等式中的舍入操作。上等式2 是分段平坦算子。解决这个问题的一种流行方法是通过所谓的直通估计器（STE）来近似该算子的梯度。STE 实质上忽略了舍入运算，并使用恒等函数对其进行近似，如下图所示。
- 量化感知训练过程的图示，包括直通估计器 (STE) 的使用。
尽管 STE 是粗略近似，但它在实践中通常表现良好，除了超低精度量化（例如二进制量化）。 [Understanding straight-through estimator in training activation quantized neural nets]的工作为这种现象提供了理论依据，并且发现STE的粗梯度近似可以预期与群体梯度相关（对于STE的正确选择）。从历史的角度来看，我们应该注意到，STE 的最初想法可以追溯到的开创性工作，其中使用恒等运算符来近似二元神经元的梯度。
虽然 STE 是主流方法，但文献中也探索了其他方法。我们首先应该提到，还提出了一种随机神经元方法作为 STE 的替代方案。还提出了使用组合优化、目标传播或Gumbelsoftmax的其他方法。另一类不同的替代方法尝试使用正则化运算符来强制量化权重。这消除了在等式2中使用不可微量化运算符的需要。这些通常被称为非 STE 方法。该领域的最新研究包括 ProxQuant ，它消除了量化公式 Eq. 2中的舍入操作。而是使用所谓的 W 形非平滑正则化函数将权重强制执行为量化值。其他值得注意的研究包括使用脉冲训练来近似不连续点的导数，或用浮点和量化参数的仿射组合替换量化权重。最近的工作还提出了 AdaRound，这是一种自适应舍入方法，作为舍入到最近方法的替代方法。尽管该领域的工作很有趣，但这些方法通常需要大量调整，到目前为止，STE 方法是最常用的方法。
除了调整模型参数之外，一些先前的工作发现在 QAT 期间学习量化参数也很有效。 PACT均匀量化下激活的剪切范围，而 QIT 还学习量化步骤和级别，作为非均匀量化设置的扩展。 LSQ 引入了一种新的梯度估计来学习 QAT 期间非负激活（例如 ReLU）的缩放因子，并且 LSQ+ 进一步将这一想法扩展到一般激活函数，例如 swish 和 h-swish 产生负值。
摘要（QAT）。尽管 STE 是粗略近似，但 QAT 已被证明是有效的。然而，QAT 的主要缺点是重新训练 NN 模型的计算成本。这种重新训练可能需要执行数百个时期才能恢复准确性，特别是对于低位精度量化。如果量化模型要长期部署，并且效率和准确性特别重要，那么重新训练的投资可能是值得的。然而，情况并非总是如此，因为某些型号的使用寿命相对较短。接下来，我们接下来讨论一种没有这种开销的替代方法。
训练后量化：昂贵的 QAT 方法的替代方法是训练后量化 (PTQ)，它执行量化和权重调整，无需任何微调。因此，PTQ 的开销非常低并且通常可以忽略不计。与 QAT 需要足够多的训练数据进行再训练不同，PTQ 还有一个额外的优点，那就是它可以应用于数据有限或未标记的情况。然而，与 QAT 相比，这通常会以较低的精度为代价，特别是对于低精度量化。
因此，人们提出了多种方法来减轻 PTQ 的准确性下降。例如，观察权重值量化后均值和方差的固有偏差，并提出偏差校正方法；和表明均衡不同层或通道之间的权重范围（和隐式激活范围）可以减少量化误差。 ACIQ 分析计算 PTQ 的最佳限幅范围和通道级位宽设置。尽管 ACIQ 可以实现较低的精度下降，但 ACIQ 中使用的通道激活量化很难在硬件上有效部署。为了解决这个问题，OMSE方法删除了激活时的通道量化，并提出通过优化量化张量和相应浮点张量之间的L2距离来进行PTQ。此外，为了更好地减轻异常值对 PTQ 的不利影响，提出了一种异常值通道分裂（OCS）方法，该方法将包含异常值的通道复制并减半。另一项值得注意的工作是 AdaRound，它表明朴素的舍入到最近的量化方法可能会违反直觉地导致次优解决方案，并且它提出了一种自适应舍入方法，可以更好地减少损失。虽然 AdaRound 将量化权重的变化限制在全精度对应物的 ±1 范围内，但 AdaQuant 提出了一种更通用的方法，允许量化权重根据需要进行更改。 PTQ 方案可以发挥到极致，在量化过程中既不使用训练数据也不使用测试数据（也称为零样本场景），这将在下面讨论。
摘要（PTQ）。在 PTQ 中，所有权重和激活量化参数都是确定的，无需对 NN 模型进行任何重新训练。因此，PTQ 是一种非常快速的量化 NN 模型的方法。然而，与 QAT 相比，这通常会以较低的准确性为代价。
3）零样本量化：正如到目前为止所讨论的，为了在量化后实现最小的精度下降，我们需要访问训练数据的全部或一小部分。首先，我们需要知道激活的范围，以便我们可以剪辑值并确定适当的缩放因子（在文献中通常称为校准）。其次，量化模型通常需要微调来调整模型参数并恢复精度下降。然而，在许多情况下，在量化过程中不可能访问原始训练数据。这是因为训练数据集要么太大而无法分发、要么是专有的（例如 Google 的 JFT-300M），要么是由于安全或隐私问题而敏感（例如医疗数据）。人们提出了几种不同的方法来应对这一挑战，我们将其称为零样本量化（ZSQ）。这里我们首先描述两种不同级别的零样本量化：
- 无数据且无微调（ZSQ + PTQ）。
- 没有数据，但需要微调（ZSQ + QA T）。
级别 1 允许更快、更轻松的量化，无需任何微调。微调通常非常耗时，并且通常需要额外的超参数搜索。然而，2 级通常会产生更高的精度，因为微调有助于量化模型恢复精度下降，特别是在超低位精度设置中。 [Data-free quantization through weight equalization and bias correction] 的工作使用了 1 级方法，该方法依赖于均衡权重范围和纠正偏差误差，使给定的 NN 模型更适合量化，而无需任何数据或微调。然而，由于该方法基于（分段）线性激活函数的尺度等方差特性，因此对于具有非线性激活的神经网络来说，它可能不是最优的，例如具有 GELU 激活的 BERT 或 MobileNetV3，带有swish激活。
ZSQ 研究的一个流行分支是生成与训练目标预训练模型的真实数据类似的合成数据。然后，合成数据用于校准和/或微调量化模型。该领域的早期工作利用生成对抗网络（GAN）来生成合成数据。使用预训练的模型作为判别器，它训练生成器，使其输出可以被判别器很好地分类。然后，使用从生成器收集的合成数据样本，可以通过从全精度对应物中提取知识来微调量化模型。然而，该方法无法捕获真实数据的内部统计数据（例如，中间层激活的分布），因为它仅使用模型的最终输出生成。不考虑内部统计的合成数据可能无法正确代表真实的数据分布。为了解决这个问题，许多后续工作使用批量归一化（BatchNorm）中存储的统计数据，即通道均值和方差，来生成更真实的合成数据。特别是，通过直接最小化内部统计的KL散度来生成数据，并使用合成数据来校准和微调量化模型。此外，ZeroQ 表明合成数据可用于灵敏度测量和校准，从而无需访问训练/验证数据即可实现混合精度训练后量化。 ZeroQ还将ZSQ扩展到对象检测任务，因为它在生成数据时不依赖于输出标签。将输入图像设置为可训练参数，并直接对其进行反向传播，直到其内部统计数据与真实数据的内部统计数据相似。更进一步，最近的研究发现训练和利用生成模型是有效的，可以更好地捕获真实数据分布并生成更真实的合成数据。
摘要（ZSQ）。零样本（又称无数据）量化执行整个量化，无需访问训练/验证数据。这对于机器学习即服务 (MLaaS) 提供商来说尤其重要，他们希望加速客户工作负载的部署，而无需访问其数据集。此外，这对于安全或隐私问题可能限制对训练数据的访问的情况很重要。

H. Stochastic Quantization

在推理过程中，量化方案通常是确定性的。然而，这并不是唯一的可能性，一些工作已经探索了用于量化感知训练的随机量化以及降低精度的训练。高层次的直觉是，与确定性量化相比，随机量化可以让神经网络探索更多。一种流行的支持论点是，小的权重更新可能不会导致任何权重变化，因为舍入操作可能始终返回相同的权重。然而，启用随机舍入可能会为神经网络提供逃脱的机会，从而更新其参数。
更正式地说，随机量化按照与权重更新幅度相关的概率向上或向下映射浮点数。例如，等式中的 Int 运算符。定义为
- $Int(x)=\left\{ \begin{aligned} &\lceil x\rceil ~~with~probability~ x-\lfloor x\rfloor, \\ &\lfloor x\rfloor ~~with~probability~ \lceil x\rceil -x\\ \end{aligned} \right.$
- 然而，这个定义不能用于二进制量化。因此，[BinaryConnect: Training deep neural networks with binary weights during propagations]将其扩展到
- $Binary(x)=\left\{ \begin{aligned} &\lceil -1\rceil ~~with~probability~ 1-\delta(x), \\ &\lfloor +1\rfloor ~~with~probability~ \delta(x)\\ \end{aligned} \right.$
- 其中Binary是将实值x二值化的函数，σ(·)是sigmoid函数。
最近，QuantNoise中引入了另一种随机量化方法。 QuantNoise 在每次前向传递期间量化权重的不同随机子集，并使用无偏梯度训练模型。这允许在许多计算机视觉和自然语言处理模型中进行较低位精度的量化，而不会显着降低精度。然而，随机量化方法的一个主要挑战是为每个权重更新创建随机数的开销，因此它们在实践中尚未广泛采用。

IV. ADVANCED CONCEPTS: QUANTIZATION BELOW 8 BITS

A. Simulated and Integer-only Quantization

部署量化神经网络模型有两种常见方法：模拟量化（又名假量化）和纯整数量化（又名定点量化）。在模拟量化中，量化后的模型参数以低精度存储，但运算（例如矩阵乘法和卷积）是用浮点运算进行的。因此，在浮点运算之前需要对量化参数进行反量化，如下图（中）所示。
- 全精度推理（左）、模拟量化推理（中）和纯整数量化推理（右）之间的比较。
因此，人们无法完全受益于具有模拟量化的快速高效的低精度逻辑。然而，在纯整数量化中，所有运算都是使用低精度整数算术执行，如上图（右）所示。这允许使用高效的整数算术来执行整个推理，而无需对任何参数或激活进行任何浮点反量化。
一般来说，使用浮点运算进行全精度推理可能有助于最终的量化精度，但这是以无法从低精度逻辑中受益为代价的。低精度逻辑在延迟、功耗和面积效率方面比全精度逻辑具有多种优势。如下图（左）所示，许多硬件处理器（包括 NVIDIA V100 和 Titan RTX）都支持低精度算术的快速处理，可以提高推理吞吐量和延迟。此外，如下图（右）所示的 45 纳米技术，低精度逻辑在能量和面积方面的效率明显更高。例如，与 FP32 加法相比，执行 INT8 加法的能源效率提高了 30 倍，面积效率提高了 116 倍。
- （左）Titan RTX 和 A100 GPU 上不同位精度逻辑的峰值吞吐量比较。（右）45nm 技术不同精度下相应的能源成本和相对面积成本的比较。正如我们所看到的，较低的精度可提供指数级更好的能源效率和更高的吞吐量。
值得注意的纯整数量化工作包括，它将批量归一化融合到前面的卷积层中，提出了一种用于具有批量归一化的残差网络的纯整数计算方法。然而，这两种方法都仅限于 ReLU 激活。 [I-bert: Integer-only bert quantization] 最近的工作通过使用整数算术逼近 GELU 、Softmax 和层归一化来解决这一限制，并进一步将纯整数量化扩展到 Transformer 架构。
二元量化是另一类纯整数量化，其中所有缩放都是使用二元数执行的，二元数是分子中具有整数值且分母中具有 2 的幂的有理数。这导致计算图只需要整数加法、乘法、位移位，而不需要整数除法。重要的是，在这种方法中，所有加法（例如残差连接）都被强制具有相同的二元尺度，这可以使加法逻辑更简单，效率更高。
摘要（模拟量化与纯整数量化）。一般来说，与模拟/伪量化相比，纯整数量化和二元量化更理想。这是因为仅整数使用较低精度的逻辑进行算术，而模拟量化使用浮点逻辑来执行运算。然而，这并不意味着假量化永远没有用。事实上，伪量化方法对于带宽限制而不是计算限制的问题可能有益，例如在推荐系统中。对于这些任务，瓶颈是内存占用和从内存加载参数的成本。因此，对于这些情况，执行假量化是可以接受的。

B. Mixed-Precision Quantization

很容易看出，当我们使用较低精度的量化时，硬件性能会提高。然而，将模型统一量化为超低精度可能会导致精度显着下降。可以通过混合精度量化来解决这个问题，在这种方法中，每一层都以不同的位精度进行量化，如下图所示。这种方法的一个挑战是，用于选择此位设置的搜索空间与层数成指数关系。人们提出了不同的方法来解决这个巨大的搜索空间。
混合精度量化的图示。在混合精度量化中，目标是将敏感且高效的层保持在较高的精度，并且仅对不敏感和低效的层应用低精度量化。效率指标取决于硬件，可能是延迟或能耗。
为每一层选择这种混合精度本质上是一个搜索问题，并且已经为此提出了许多不同的方法。最近的工作提出了一种基于强化学习（RL）的方法来自动确定量化策略，作者使用硬件模拟器在 RL 代理反馈中获取硬件加速器的反馈。论文[Mixed precision quantization of convnets via differentiable neural architecture search]将混合精度配置搜索问题表述为神经架构搜索（NAS）问题，并使用可微分NAS（DNAS）方法来有效地探索搜索空间。这些基于探索的方法的一个缺点是它们通常需要大量的计算资源，并且它们的性能通常对超参数甚至初始化敏感。
另一类混合精度方法使用周期函数正则化来训练混合精度模型，方法是在学习各自的位宽时自动区分不同的层及其在准确性方面的不同重要性。
与这些基于探索和正则化的方法不同，HAWQ 引入了一种基于模型二阶灵敏度自动查找混合精度设置的方法。理论上表明，二阶算子（即 Hessian）的迹可用于测量层对量化的敏感度，类似于 Optimal Brain Damage 的开创性工作中的剪枝结果。在 HAWQv2 中，该方法被扩展到混合精度激活量化，并且比基于 RL 的混合精度方法快 100 倍以上。最近，在 HAWQv3 中，引入了仅整数、硬件感知的量化，该量化提出了一种快速整数线性规划方法，用于为给定的应用程序特定约束（例如，模型大小或延迟）找到最佳位精度。这项工作还通过直接将混合精度量化部署在 T4 GPU 上解决了有关混合精度量化的硬件效率的常见问题，与 INT8 量化相比，混合精度 (INT4/INT8) 量化的速度提高了 50%。
摘要（混合精度量化）。混合精度量化已被证明是一种有效且硬件高效的方法，适用于不同神经网络模型的低精度量化。在这种方法中，神经网络的层被分组为对量化敏感/不敏感，并且每层使用较高/较低位。因此，人们可以最大限度地减少精度下降，并且仍然受益于减少的内存占用和通过低精度量化实现的更快的加速。最近的工作 [Hawqv3: Dyadic neural network quantization] 还表明，这种方法具有硬件效率，因为混合精度仅跨操作/层使用。

C. Hardware Aware Quantization

量化的目标之一是改善推理延迟。然而，并非所有硬件在量化某个层/操作后都提供相同的速度。事实上，量化的好处取决于硬件，片上内存、带宽和缓存层次结构等许多因素都会影响量化速度。
为了通过硬件感知量化实现最佳效益，考虑这一事实非常重要。特别是，该工作[HAQ: Hardware-aware automated quantization]使用强化学习代理来根据不同位宽的不同层的延迟查找表来确定用于量化的硬件感知混合精度设置。然而，这种方法使用模拟硬件延迟。为了解决这个问题，[Hawqv3]最近的工作直接在硬件中部署量化操作，并测量不同量化位精度的每层的实际部署延迟。

D. Distillation-Assisted Quantization

量化领域的一个有趣的工作是结合模型蒸馏来提高量化精度。模型蒸馏是一种以更高精度的大型模型作为教师来帮助训练紧凑的学生模型的方法。在学生模型的训练过程中，模型蒸馏建议利用教师产生的软概率，而不是仅使用真实类别标签，其中可能包含更多的输入信息。也就是说，总体损失函数包含了学生损失和蒸馏损失，其通常表述如下：
- $L=\alpha H(y,\delta(z_s))+\beta H(\delta(z_t,T),\delta(z_s,T))$
- 在等式中。 α和β是调整学生模型损失量和蒸馏损失的权重系数，y是真实类标签，H是交叉熵损失函数，zs/zt是学生/老师生成的logits模型中，σ是softmax函数，T是其温度，定义如下：
- $p_i=\frac{exp\frac{z_i}{T}}{\sum_jexp\frac{z_j}{T}}$
- 以前的知识蒸馏方法侧重于探索不同的知识源。使用logits（软概率）作为知识来源，尝试利用中间层的知识。教师模型的选择也得到了很好的研究，使用多个教师模型来共同监督学生模型，应用自蒸馏而无需额外的教师模型。

E. Extreme Quantization

二值化是最极端的量化方法，其中量化值被限制为 1 位表示，从而将内存需求大幅减少 32 倍。除了内存优势之外，二进制（1 位）和三进制（2 位）运算通常可以通过逐位算术进行有效计算，并且可以在更高精度（例如 FP32 和 INT8）上实现显着加速。例如，NVIDIA V100 GPU 上的峰值二进制运算比 INT8 高 8 倍。然而，简单的二值化方法会导致精度显着下降。因此，有大量的工作提出了不同的解决方案来解决这个问题。
这里的一项重要工作是 BinaryConnect ，它将权重限制为 +1 或 -1。在这种方法中，权重保持为真实值，并且仅在前向和后向传递过程中进行二值化以模拟二值化效果。在前向传递过程中，根据符号函数将实值权重转换为+1或-1。然后可以使用标准训练方法和 STE 来训练网络，以通过不可微的符号函数传播梯度。二值化神经网络（BNN）通过二值化激活和权重扩展了这个想法。联合二值化权重和激活具有改善延迟的额外好处，因为昂贵的浮点矩阵乘法可以替换为轻量级 XNOR 运算，然后进行位计数。另一项有趣的工作是[Gxnor-net: Training deep neural networks with ternary weights and activations without full-precision memory under a unified discretization framework]中提出的二进制权重网络（BWN）和XNORNet，它们通过将缩放因子合并到权重中并使用+α或-α而不是+1或-1来实现更高的精度。这里，α 是选择的缩放因子，用于最小化实值权重和生成的二值化权重之间的距离。换句话说，实值权重矩阵 W 可以表示为 W ≈ αB，其中 B 是满足以下优化问题的二元权重矩阵：
- $\alpha,B=argmin||W-\alpha B||^2$
- 此外，受到许多学习权重接近于零的观察的启发，人们尝试通过使用三元值（例如+1、0和-1）约束权重/激活来对网络进行三元化，从而明确允许量化值是零。三值化还通过消除二值化那样昂贵的矩阵乘法来大大减少推理延迟。后来，（TBN）表明结合二元网络权重和三元激活可以实现准确性和计算效率之间的最佳权衡。
由于朴素的二值化和三值化方法通常会导致严重的精度下降，特别是对于 ImageNet 分类等复杂任务，因此人们提出了许多解决方案来减少极端量化中的精度下降。 [Binary neural networks: A survey]的工作将这些解决方案大致分为三个分支。
- a）量化误差最小化：解决方案的第一个分支旨在最小化量化误差，即实际值和量化值之间的差距。 HORQ和 ABC-Net没有使用单个二进制矩阵来表示实值权重/激活，而是使用多个二进制矩阵的线性组合，即 W ≈ α1B1 + · · · + αMBM，以减少量化误差。受到二值化激活会降低其对后续卷积块的表示能力这一事实的启发，更广泛的网络（即具有更多滤波器数量的网络）的二值化可以在精度和模型尺寸。
- b）改进的损失函数：工作的另一个分支侧重于损失函数的选择。这里的重要工作是损失感知的二值化和三值化，它们直接最小化二值化/三值化权重的损失。这与其他仅近似权重而不考虑最终损失的方法不同。全精度教师模型的知识蒸馏也被证明是一种有前途的方法，可以恢复二值化/三值化后的精度下降。
- c）改进的训练方法：另一个有趣的工作分支旨在为二元/三元模型提供更好的训练方法。许多研究指出了 STE 通过符号函数反向传播梯度的局限性：STE 仅传播 [-1, 1] 范围内的权重和/或激活的梯度。为了解决这个问题，BNN+[Bnn+: Improved binary network training]引入了符号函数导数的连续近似，用平滑、可微的函数代替符号函数，逐渐锐化并接近符号函数。 Bi-Real Net 引入了将激活连接到连续块中的激活的身份快捷方式，通过它可以传播32位激活。虽然大多数研究的重点是减少推理时间延迟，但 DoReFa-Net 除了权重和激活之外还量化梯度，以加速训练。
极端量化已成功大幅减少计算机视觉任务中许多 CNN 模型的推理/训练延迟以及模型大小。最近，有人尝试将这一想法扩展到自然语言处理（NLP）任务中。考虑到最先进的 NLP 模型（例如 BERT 、RoBERTa 和 GPT 系列）的模型大小和推理延迟令人望而却步，这些模型是在由于存在大量未标记数据，极端量化正在成为将 NLP 推理任务推向边缘的强大工具。
摘要（极端量化）。极低位精度量化是一个非常有前途的研究领域。然而，与基线相比，现有方法通常会导致高精度下降，除非执行非常广泛的调整和超参数搜索。但对于不太关键的应用来说，这种精度下降可能是可以接受的。

F . Vector Quantization

正如第二部分所讨论的，量化并不是在机器学习中发明的，但在过去的一个世纪中在信息论中得到了广泛的研究，特别是在数字信号处理领域作为一种压缩工具。然而，机器学习量化方法之间的主要区别在于，从根本上来说，我们不希望以与原始信号相比最小的变化/误差来压缩信号。相反，目标是找到一种降低精度的表示，从而导致尽可能小的损失。因此，如果量化的权重/激活远离非量化的权重/激活，这是完全可以接受的。
话虽如此，DSP 中的经典量化方法中有很多有趣的想法已应用于 NN 量化，特别是矢量量化。特别是，有一些工作将权重聚类到不同的组中，并在推理过程中使用每个组的质心作为量化值。如下方程式所示。i是张量中权重的索引，c1，…，ck是聚类找到的k个质心，cj是wi对应的质心。聚类后，权重wi将在码本（查找表）中具有与cj相关的聚类索引j。
- $\min_{c_1,...,c_k}\sum_i||w_i-c_j||^2$
- 研究发现，使用 k 均值聚类足以将模型大小减小至 8 倍，而不会显着降低精度。除此之外，联合应用基于 k 均值的矢量量化与剪枝和霍夫曼编码可以进一步减小模型大小。
乘积量化是矢量量化的扩展，其中权重矩阵被划分为子矩阵并对每个子矩阵应用矢量量化。除了基本的乘积量化方法外，更细粒度的聚类使用可以进一步提高准确性。在[Compressing deep convolutional networks using vector quantization]中，k均值乘积量化后的残差被进一步递归量化。在[Weighted-entropy-based quantization for deep neural networks]中，作者将更多的聚类应用于更重要的量化范围，以更好地保存信息。

V. QUANTIZATION AND HARDWARE PROCESSORS

量化不仅可以减小模型大小，而且还可以实现更快的速度和更低的功耗，特别是对于具有低精度逻辑的硬件。因此，量化对于物联网和移动应用的边缘部署尤其重要。边缘设备通常具有严格的资源限制，包括计算、内存，以及重要的功耗预算。对于许多深度神经网络模型来说，满足这些要求通常成本太高。此外，许多边缘处理器不支持浮点运算，特别是在微控制器中。
在这里，我们简要讨论量化背景下的不同硬件平台。 ARM Cortex-M 是一组 32 位 RISC ARM 处理器内核，专为低成本、高能效的嵌入式设备而设计。例如，STM32 系列是基于 ARM Cortex-M 内核的微控制器，也用于边缘的神经网络推理。由于某些 ARM Cortex-M 内核不包含专用浮点单元，因此在部署之前应首先对模型进行量化。 CMSIS-NN 是 ARM 的一个库，可帮助量化 NN 模型并将其部署到 ARM Cortex-M 内核上。具体来说，该库利用具有二次方缩放因子的定点量化，以便可以通过移位操作有效地执行量化和反量化过程。 GAP-8是一款带有专用 CNN 加速器的用于边缘推理的 RISC-V SoC（片上系统），是仅支持整数运算的边缘处理器的另一个示例。虽然可编程通用处理器因其灵活性而被广泛采用，但 Google Edge TPU（一种专用 ASIC 芯片）是另一种在边缘运行推理的新兴解决方案。与运行在拥有大量计算资源的 Google 数据中心的 Cloud TPU 不同，Edge TPU 是为小型低功耗设备设计的，因此仅支持 8 位算术。神经网络模型必须使用 TensorFlow 的量化感知训练或训练后量化进行量化。
下图绘制了广泛用于边缘神经网络推理的不同商业边缘处理器的吞吐量。在过去的几年里，边缘处理器的计算能力有了显着的提高，这使得以前只能在服务器上使用的昂贵的神经网络模型得以部署和推理。量化与高效的低精度逻辑和专用深度学习加速器相结合，一直是此类边缘处理器发展的重要驱动力之一。
- 不同商用边缘处理器在边缘进行神经网络推理的吞吐量比较。
虽然量化对于许多边缘处理器来说是必不可少的技术，但它也可以为非边缘处理器带来显着的改进，例如满足服务级别协议（SLA）要求，例如 99% 延迟。最近的 NVIDIA 图灵 GPU 就是一个很好的例子，特别是 T4 GPU，其中包括图灵张量核心。张量核心是专门为高效低精度矩阵乘法而设计的执行单元。

VI. FUTURE DIRECTIONS FOR RESEARCH IN QUANTIZATION

在这里，我们简要讨论量化未来研究的几个高级挑战和机遇。这分为量化软件、硬件和神经网络架构协同设计、耦合压缩方法和量化训练。
量化软件：使用当前方法，可以直接量化不同的神经网络模型并将其部署到 INT8，而不会损失准确性。有几个软件包可用于部署 INT8 量化模型（例如 Nvidia 的 TensorRT、TVM 等），每个软件包都有很好的文档。此外，这些实现也是相当优化的，并且可以很容易地观察到量化带来的速度提升。然而，用于较低位精度量化的软件并不广泛可用，有时甚至不存在。例如，Nvidia 的 TensorRT 目前不支持 sub-INT8 量化。此外，TVM 最近才添加了对 INT4 量化的支持。最近的工作表明，使用 INT4/INT8 进行低精度和混合精度量化在实践中是可行的。因此，开发用于较低精度量化的高效软件 API 将产生重要影响。
硬件和神经网络架构协同设计：如上所述，低精度量化的经典工作与机器学习的最新工作之间的一个重要区别是，神经网络参数可能具有非常不同的量化值，但仍然可以很好地概括。例如，通过量化感知训练，我们可能会收敛到不同的解决方案，远离具有单精度参数的原始解决方案，但仍然获得良好的准确性。人们可以利用这种自由度，并在量化时调整神经网络架构。例如，最近的工作表明，改变神经网络架构的宽度可以减少/消除量化后的泛化差距。未来的工作之一是在模型量化时联合调整其他架构参数，例如深度或单个内核。未来的另一项工作是将这种协同设计扩展到硬件架构。这对于 FPGA 部署可能特别有用，因为人们可以探索许多不同的可能硬件配置（例如乘法累加元素的不同微架构），然后将其与 NN 架构和量化协同设计结合起来。
耦合压缩方法：如上所述，量化只是有效部署神经网络的方法之一。其他方法包括高效的神经网络架构设计、硬件和神经网络架构的协同设计、剪枝和知识蒸馏。量化可以与这些其他方法结合使用。然而，目前很少有工作探索这些方法的最佳组合。例如，剪枝和量化可以一起应用于模型以减少其开销，并且了解结构化/非结构化剪枝和量化的最佳组合非常重要。同样，未来的另一个方向是研究这些方法与上述其他方法之间的耦合。
量化训练：也许量化最重要的用途是加速半精度的神经网络训练。这使得能够使用更快、更省电的低精度逻辑进行训练。然而，将其进一步推向 INT8 精确训练是非常困难的。虽然该领域存在一些有趣的工作，但所提出的方法通常需要大量的超参数调整，或者它们仅适用于相对简单的学习任务上的一些神经网络模型。基本问题是，对于 INT8 精度，训练可能会变得不稳定和发散。解决这一挑战可能会对多种应用产生重大影响，尤其是边缘训练。

VII. SUMMARY AND CONCLUSIONS

一旦抽象数学计算适应数字计算机上的计算，这些计算中数值的有效表示、操作和通信问题就出现了。与数值表示问题密切相关的是量化问题：一组连续实值数应该以什么方式分布在一组固定的离散数上，以最小化所需的位数并最大化量化的精度。随之而来的计算？虽然这些问题与计算机科学一样古老，但这些问题与高效神经网络模型的设计尤其相关。有几个原因。首先，神经网络是计算密集型的。因此，数值的有效表示就显得尤为重要。其次，大多数当前的神经网络模型都严重过度参数化。因此，有足够的机会在不影响精度的情况下降低位精度。第三，神经网络模型的分层结构提供了一个额外的探索维度。因此，神经网络中的不同层对损失函数有不同的影响，这激发了混合精度量化等有趣的方法。
从浮点表示转向以八/四位或更少位表示的低精度固定整数值有可能减少内存占用和延迟。流行的计算机视觉模型的INT8推理，包括使用TVM 量化库的ResNet50 、VGG-19 和inceptionV3 ，可以实现3.89×、3.32×和5.02×分别在 NVIDIA GTX 1080 上实现加速。与 INT8 对应物相比，ResNet50 的 INT4 推理可以在 NVIDIA T4 和 RTX 上带来 50-60% 的额外加速，强调了使用较低位精度来最大化效率的重要性。
最近，Hawqv3 利用混合精度量化，与没有精度下降的 INT8 推理相比，ResNet50 实现了 23% 的加速，并且将仅 INT8 推理扩展到 BERT 模型，使推理速度比 FP32 快 4.0 倍。虽然上述工作重点关注 GPU 上的加速，[Efficient execution of quantized deep learning models: A compiler approach.] 还通过各种计算机视觉模型的 INT8 量化，在 Intel Cascade Lake CPU 和 Raspberry Pi4（均为非 GPU 架构）上分别获得了 2.35× 和 1.40× 的延迟加速。因此，正如我们的参考书目所证明的那样，神经网络模型中的量化问题一直是一个非常活跃的研究领域。
在这项工作中，我们试图为这些非常多样化的工作带来一些概念结构。我们首先讨论许多量化应用中常见的主题，例如均匀、非均匀、对称、非对称、静态和动态量化。然后我们考虑了神经网络量化更独特的量化问题。这些包括分层、分组、通道和子通道量化。我们进一步考虑了训练和量化之间的相互关系，并讨论了量化感知训练与训练后量化相比的优点和缺点。进一步细致化量化和训练之间关系的讨论是数据的可用性问题。这种情况的极端情况是，由于隐私等各种合理原因，训练中使用的数据不再可用。这引发了零样本量化问题。
由于我们特别关注针对边缘部署的高效神经网络，因此我们考虑了该环境特有的问题。其中包括量化技术，这些技术会导致参数用少于 8 位（可能低至二进制值）表示。我们还考虑了纯整数量化的问题，这使得神经网络能够部署在通常缺乏浮点单元的低端微处理器上。
一般情况下，参数剪枝，特别是非结构化剪枝，能大大压缩模型大小，且不容易丢失分类精度。对于需要稳定的模型分类的应用，非结构化剪枝成为首要选择。如果需要一次性端对端训练得到压缩与加速后模型，可以利用基于紧性滤波设计的深度神经网络压缩与加速方法。影响神经网络推理速度主要有 4 个因素：计算量 FLOPs、内存访问代价 MAC、计算并行度、硬件平台架构与特性（算力、GPU 内存带宽）。