二叉树链式结构的实现—

一、提前说明

二、二叉树的遍历

2.1前序遍历

2.2中序遍历

2.3后序遍历

2.4代码

三、二叉树结点个数

3.1整体思路

3.2代码

四、二叉树叶子结点个数

4.1整体思路

4.2代码

五、二叉树的高度(深度)

5.1整体思路

5.2代码

六、二叉树第k层节点个数

6.1整体思路：

6.2代码

七、二叉树查找值为x的节点

7.1整体思路

7.2代码

八、二叉树的创建

8.1整体思路编辑

8.2代码

九、二叉树的销毁

十、二叉树的层序遍历

10.1层序遍历的概念

编辑10.2整体思路

10.3代码

10.4番外篇

十一、检查二叉树是否为完全二叉树

11.1整体思路

11.2代码

一、提前说明

在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。我们在这里先手动构建一棵“死树”，学完基本操作以后我们再来重新构建。

typedef int BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}TreeNode;

TreeNode* CreateTreeNode(int x)
{
	TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
	assert(node);

	node->data = x;
	node->left = NULL;
	node->right = NULL;

	return node;
}

TreeNode* CreateTree()
{
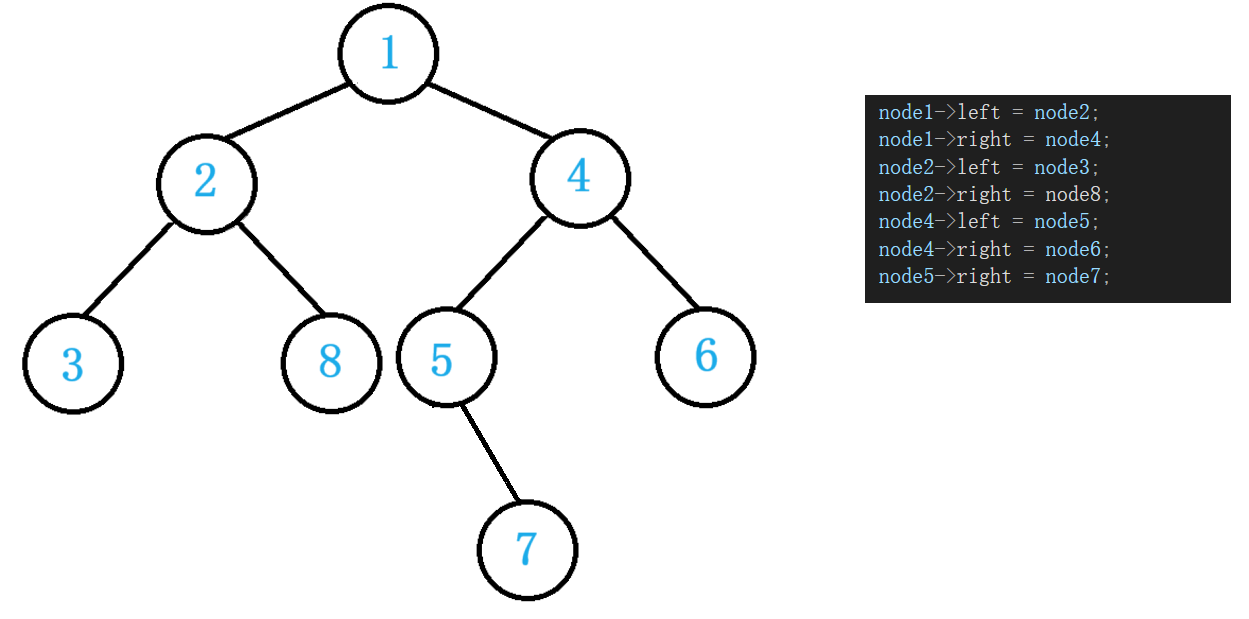
	TreeNode* node1 = CreateTreeNode(1);
	TreeNode* node2 = CreateTreeNode(2);
	TreeNode* node3 = CreateTreeNode(3);
	TreeNode* node4 = CreateTreeNode(4);
	TreeNode* node5 = CreateTreeNode(5);
	TreeNode* node6 = CreateTreeNode(6);
	TreeNode* node7 = CreateTreeNode(7);


	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	node5->right = node7;

	return node1;
}

二、二叉树的遍历

遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础

2.1前序遍历

前序遍历(Preorder Traversal)——访问根结点的操作发生在遍历其左右子树之前。

2.2中序遍历

中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

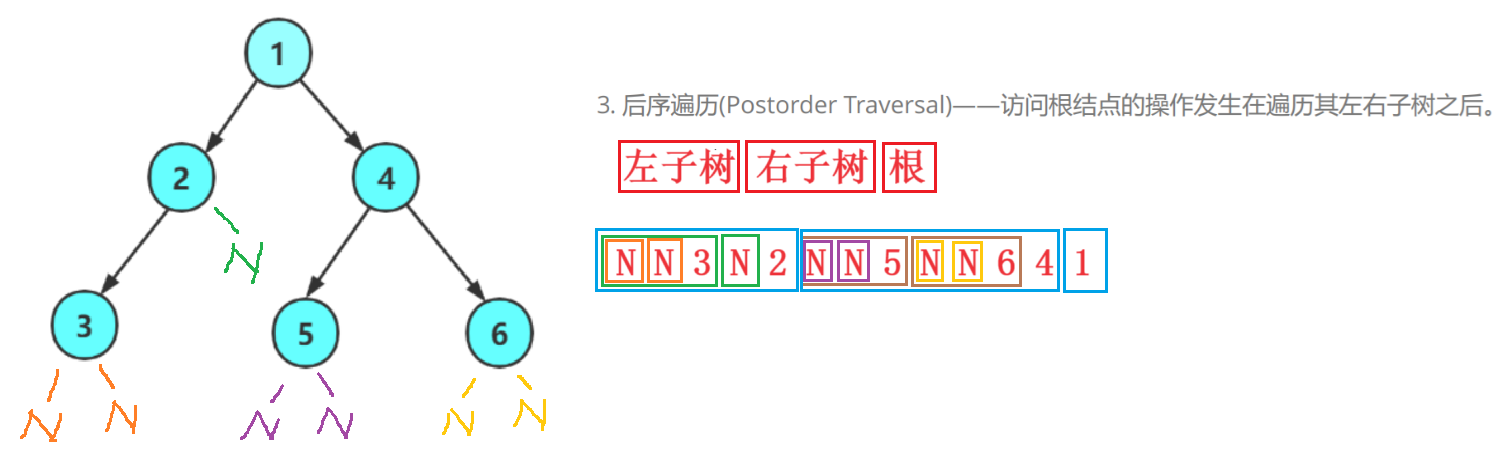
2.3后序遍历

后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

2.4代码

void PreOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

void InOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

紧接着我们用我们的“死树”来验证一下我们的代码：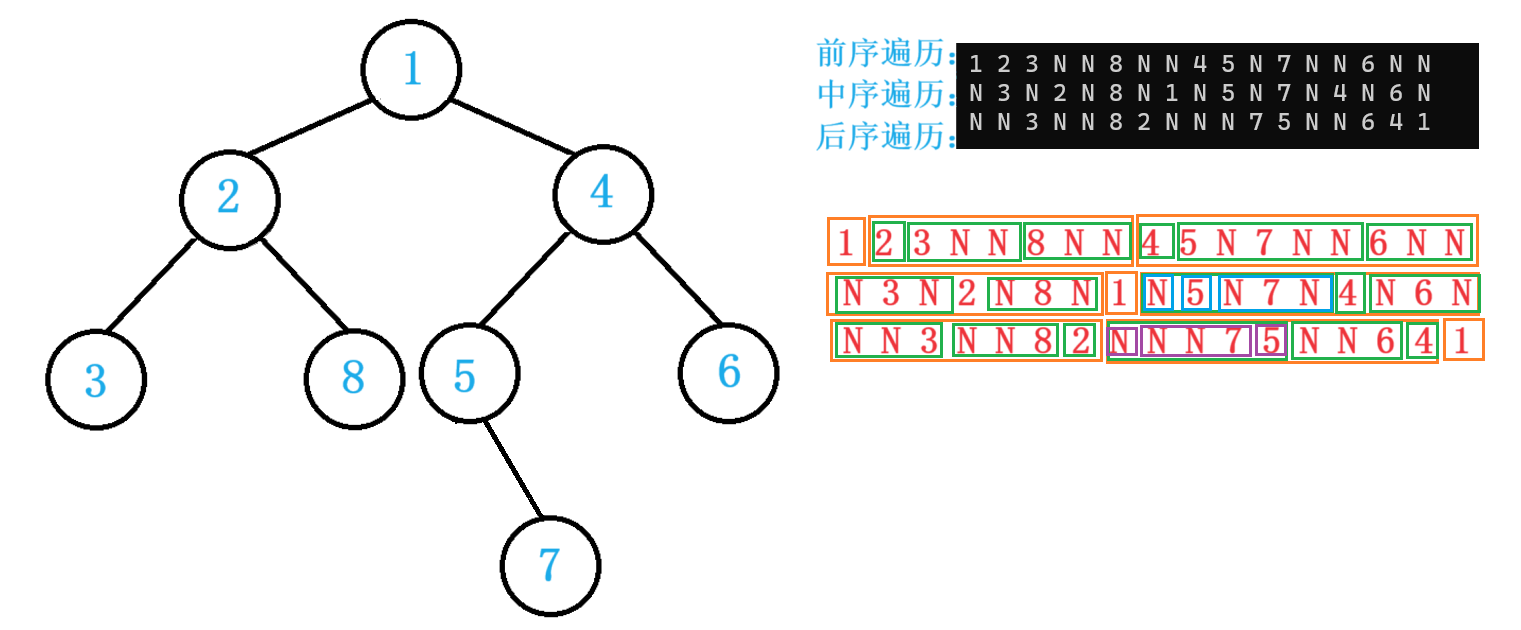

我们看我们的二叉树其实是非常丑的，但是我们通过验证也证明了我们代码的正确性。

而且在验证的时候还有一个小插曲：当我发现实际和输出不对等时，我没有怀疑代码的正确性，而是发现我的二叉树图画错了。

三、二叉树结点个数

3.1整体思路

求结点个数那么遍历整个二叉树肯定是必要的，这就是为什么说遍历是最重要的操作的原因

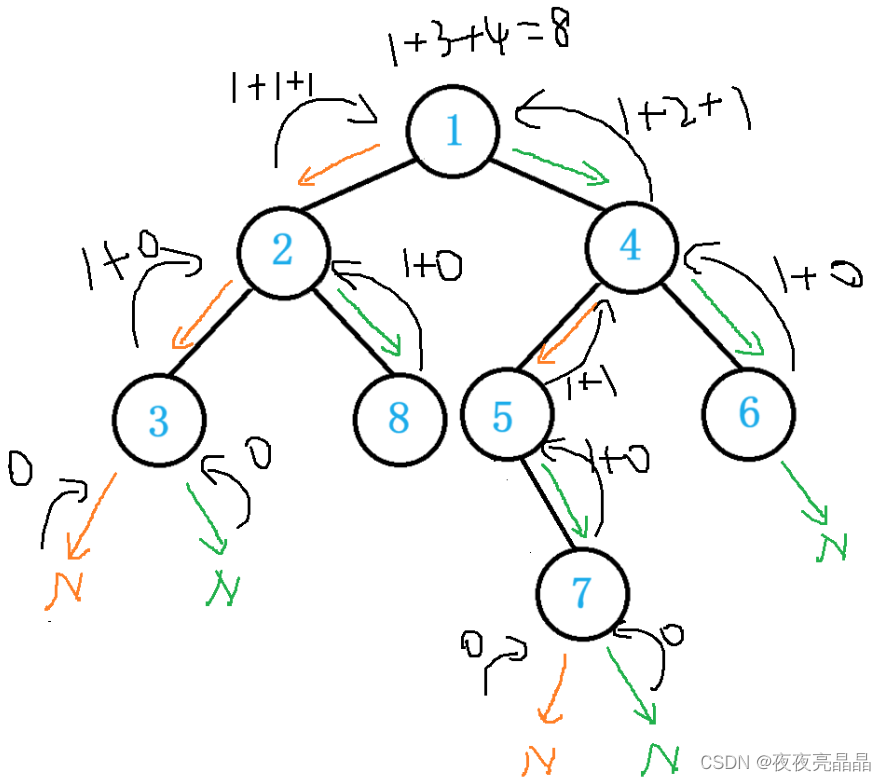
我们可以看出，如果root为NULL时，返回0，否则都是向上返回左右结点之和，那么我们就可以直接相加，还要加上它本身。

3.2代码

int BinaryTreeSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

四、二叉树叶子结点个数

叶结点或终端结点：度为0的节点称为叶节点

4.1整体思路

我们的想法是上一个函数的基础上修改一下返回条件：

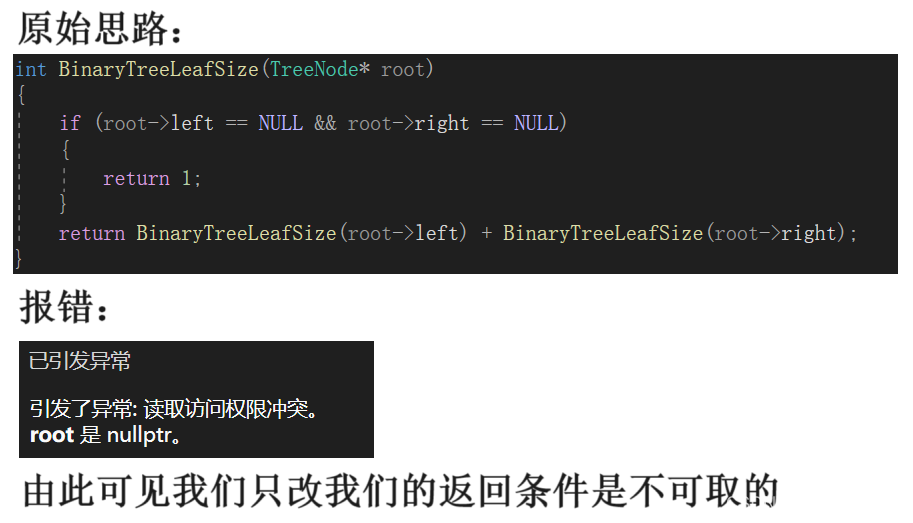
4.2代码

int BinaryTreeLeafSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

五、二叉树的高度(深度)

5.1整体思路

首先要判断根是否存在，如果根存在，继续向下遍历，再次遍历的时候，先判断其左右子树是否存在，若存在，再遍历其左右子树，此时就不用再进行根判断了，根判断的代码只在进入函数时有效执行。以下是我们的大致思路，但是递归的图着实太难画了，实在不理解可以仔细参照文字或者自己画：

在画图的过程中我们也发现了，我们每次都要返回左右子树遍历后的较大值，如何做？

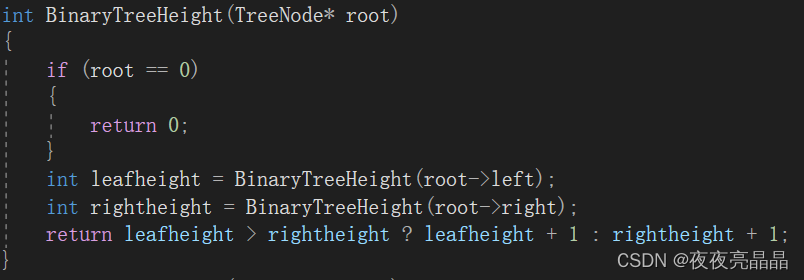
这时我们可以借用C语言库中的较大值函数，而且可以进行代码的简化：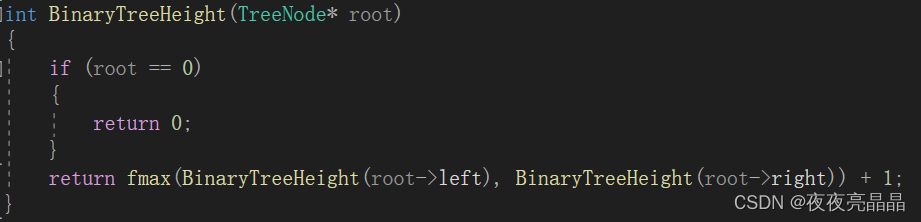

5.2代码

int BinaryTreeHeight(TreeNode* root)
{
	if (root == 0)
	{
		return 0;
	}
	return fmax(BinaryTreeHeight(root->left), BinaryTreeHeight(root->right)) + 1;
}

六、二叉树第k层节点个数

6.1整体思路：

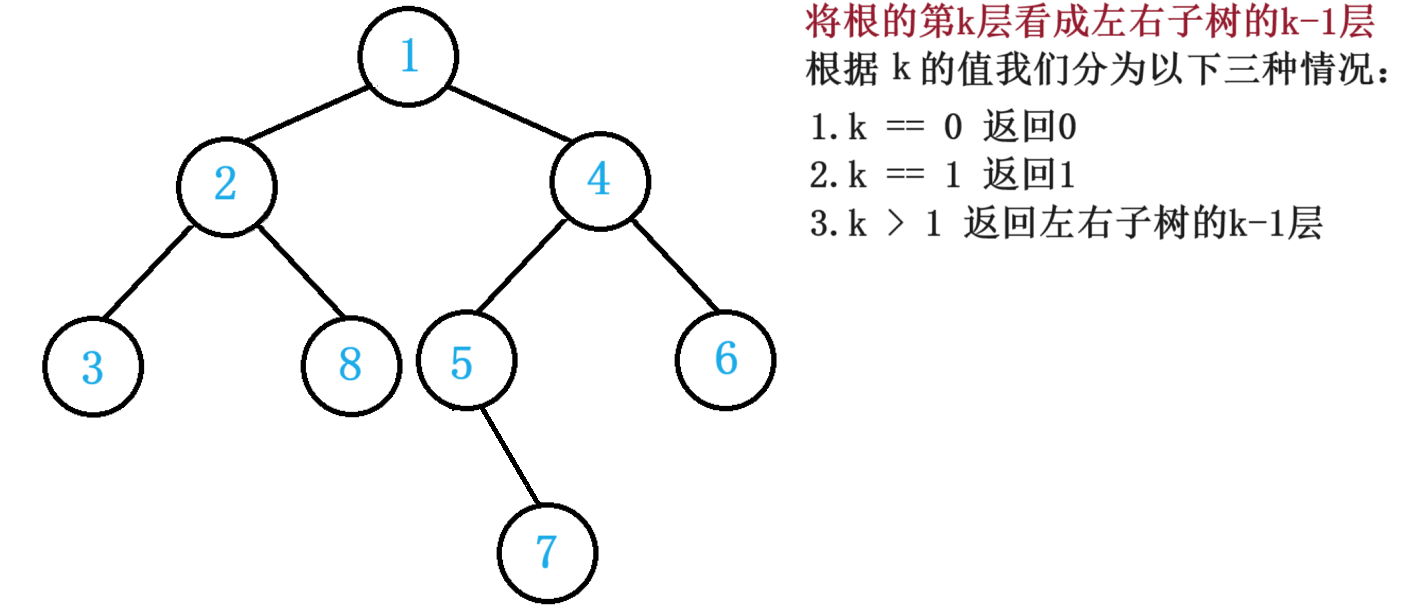
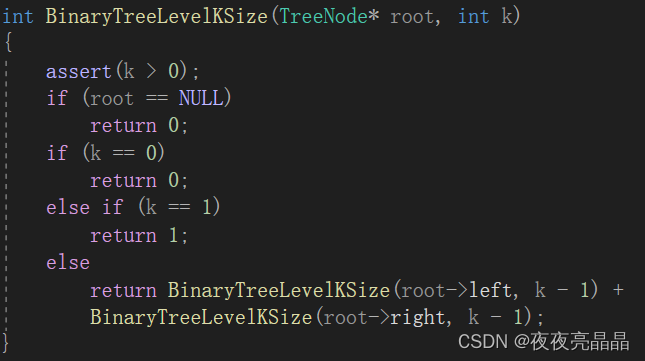
6.2代码

int BinaryTreeLevelKSize(TreeNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
		return 0;
	if (k == 0)
		return 0;
	else if (k == 1)
		return 1;
	else
		return BinaryTreeLevelKSize(root->left, k - 1) + 
		BinaryTreeLevelKSize(root->right, k - 1);
}

七、二叉树查找值为x的节点

7.1整体思路

我认为思路的重点是怎么递归左右子树并当返回其中不为空的值。

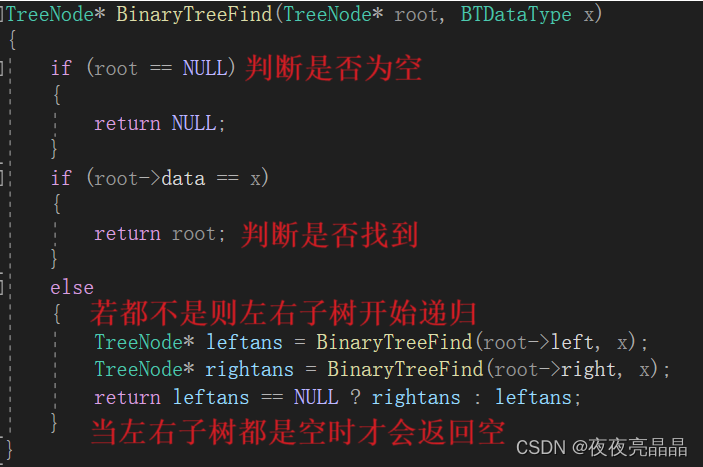
我们要如何验证代码的正确性呢？在return 0处打断点：

另外我们的printf要用p%打印出地址，观察监视的值与输出是否相同。

7.2代码

TreeNode* BinaryTreeFind(TreeNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	else
	{
		TreeNode* leftans = BinaryTreeFind(root->left, x);
		TreeNode* rightans = BinaryTreeFind(root->right, x);
		return leftans == NULL ? rightans : leftans;
	}
}

八、二叉树的创建

我们以前序遍历为例子，假设我们提供一个数组“123NN8NN45N7NN6NN”，需要以前序遍历来恢复这棵二叉树，我们要怎么办呢？

8.1整体思路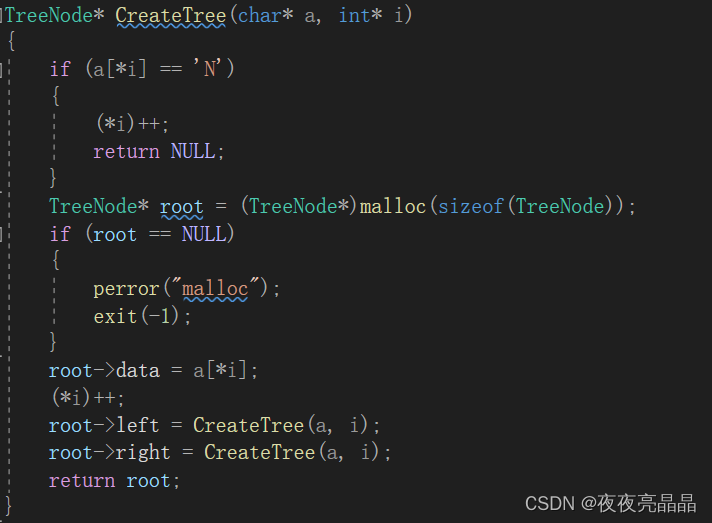

其中需要注意的点是，因为我们要辨别空指针，所以我们传的是一个 char 数组，因为我们 root 接收的永远是数组中的元素，所以我们要有一个能每次递归都改变值的下标 i ，所以我们使用了传址调用的方式来调用 i

但是我们代码的正确性怎么检查呢？各位可以专门写一个打印函数，把它打印出来，我就偷个懒，打了断点来监视，根据监视画了图：

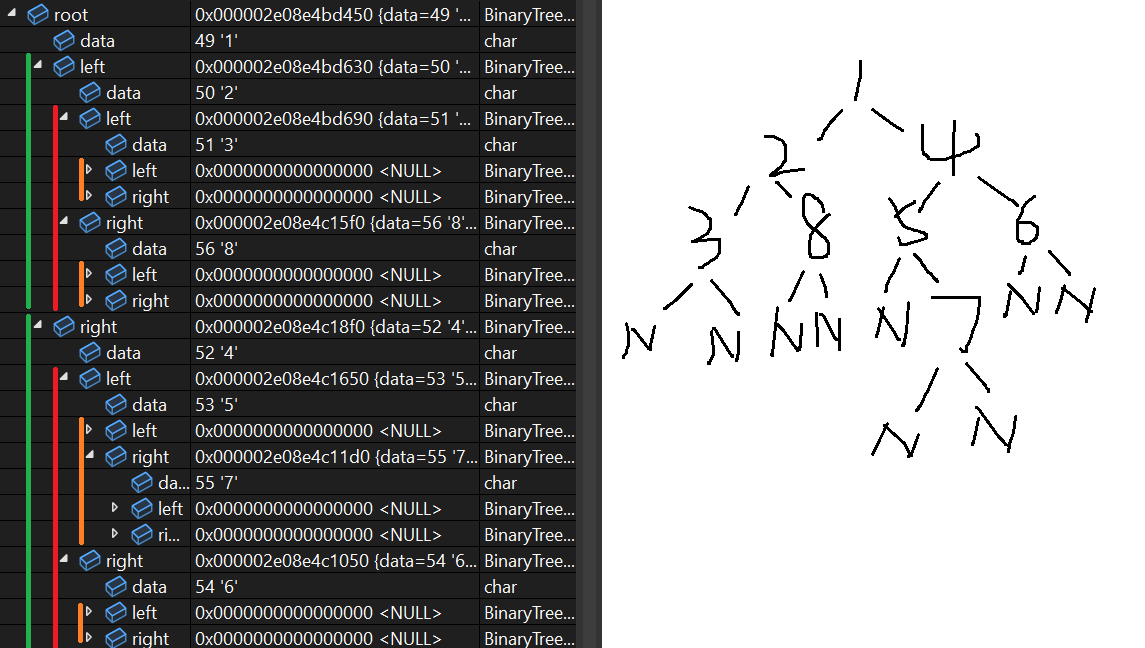
大家看这个图是不是有点眼熟（虽然我画的比较丑），但前序遍历的数组我就是抄之前的代码，现在我把之前的“死树”粘贴过来，大家对比一下，根据监视窗口画出来的树和实际的树是不是完全一样？

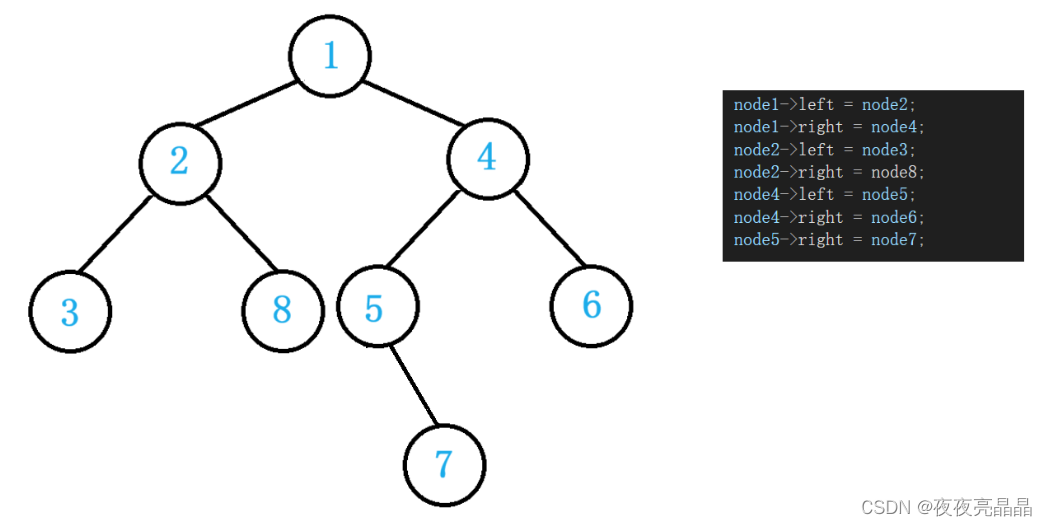
8.2代码

TreeNode* CreateTree(char* a, int* i)
{
	if (a[*i] == 'N')
	{
		(*i)++;
		return NULL;
	}
	TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
	if (root == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	root->data = a[*i];
	(*i)++;
	root->left = CreateTree(a, i);
	root->right = CreateTree(a, i);
	return root;
}

九、二叉树的销毁

二叉树的销毁就容易多了，我们直接看代码吧！

void DestroyTree(TreeNode* root)
{
	if (root == NULL)
		return;
	DestroyTree(root->left);
	DestroyTree(root->right);
	free(root);
	root = NULL;
}

十、二叉树的层序遍历

10.1层序遍历的概念

其实二叉树并非只有前中后序的遍历，还有层序遍历，即使我们的二叉树一层一层的输出：

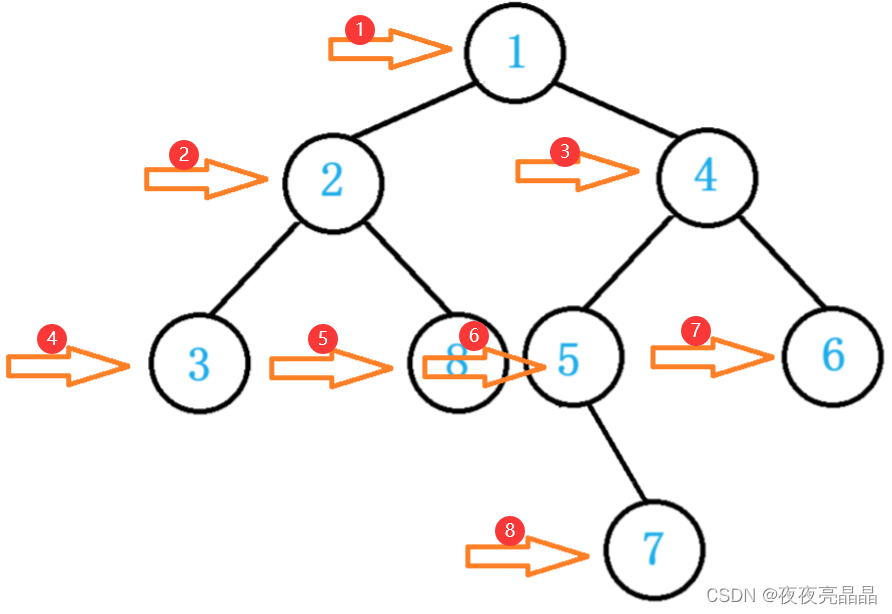10.2整体思路

我们可以用队列来实现，当我们的根被Pop时，就把他的两个子结点Push入队，以此类推，大家看图吧！

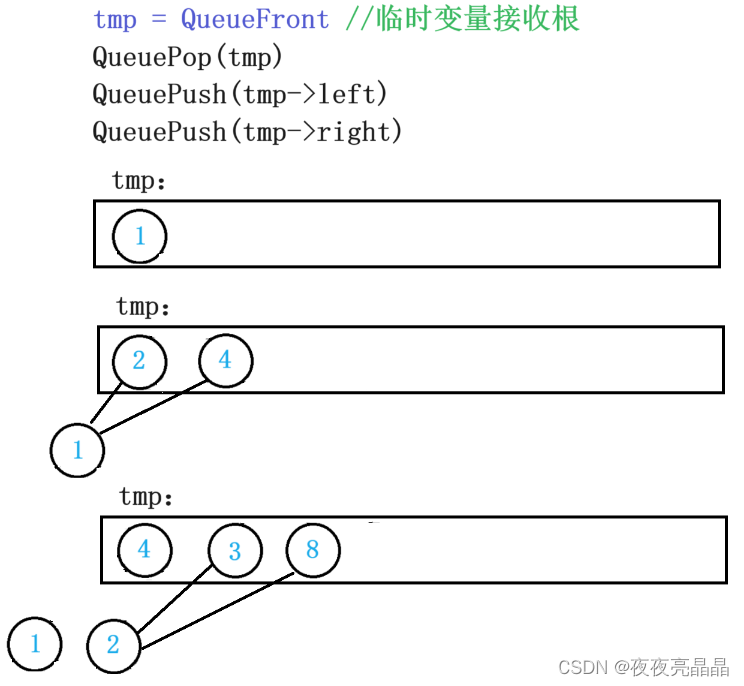
我们先把之前写的队列的代码Copy一份放在我们现在的代码中：

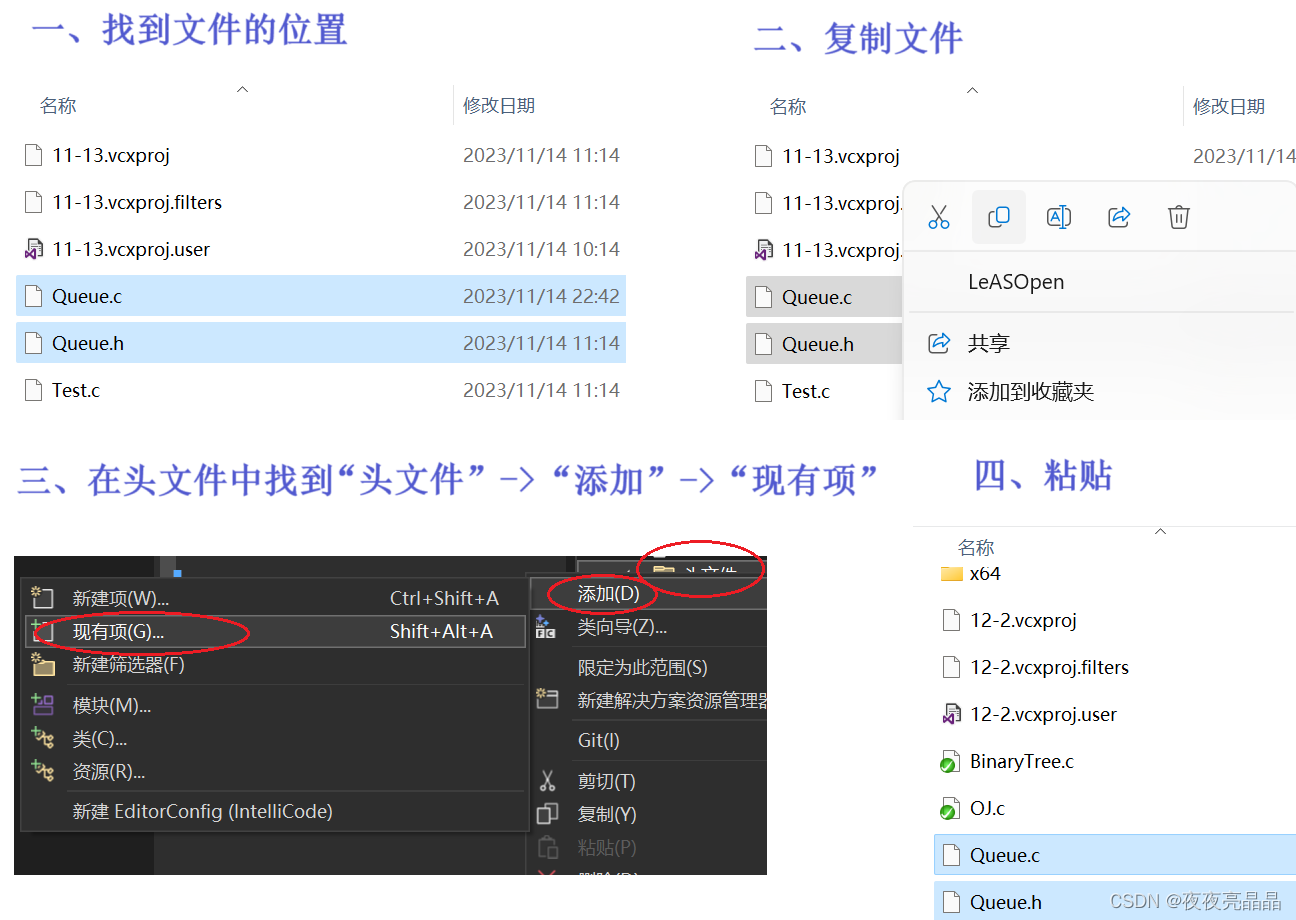接着我们就可以在右侧列表中看到我们的Queue了！

因为我们使用的是队列，所以千万别忘了使用队列前的操作：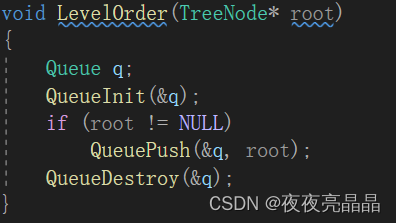
因为我们使用队列存放的是二叉树的结点，所以我们的QueueDataType也要改为Tree Node* !
接着我们就可以写出下面的代码，经过测试，不论死树还是活树，我们的层序遍历都是对的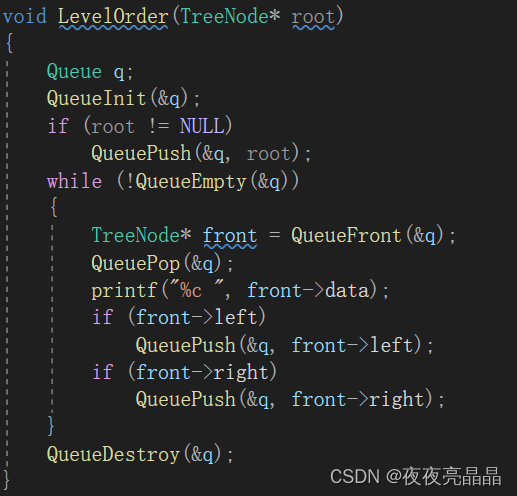

10.3代码

void LevelOrder(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root != NULL)
		QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->data);
		if (front->left)
			QueuePush(&q, front->left);
		if (front->right)
			QueuePush(&q, front->right);
	}
	QueueDestroy(&q);
}

10.4番外篇

我们来看一下我们的层序遍历的输出，这个输出好像有点丑，明明是层序输出，但是为什么那么没有层次感呢？下面请我们思考一下如何一层一层的输出呢？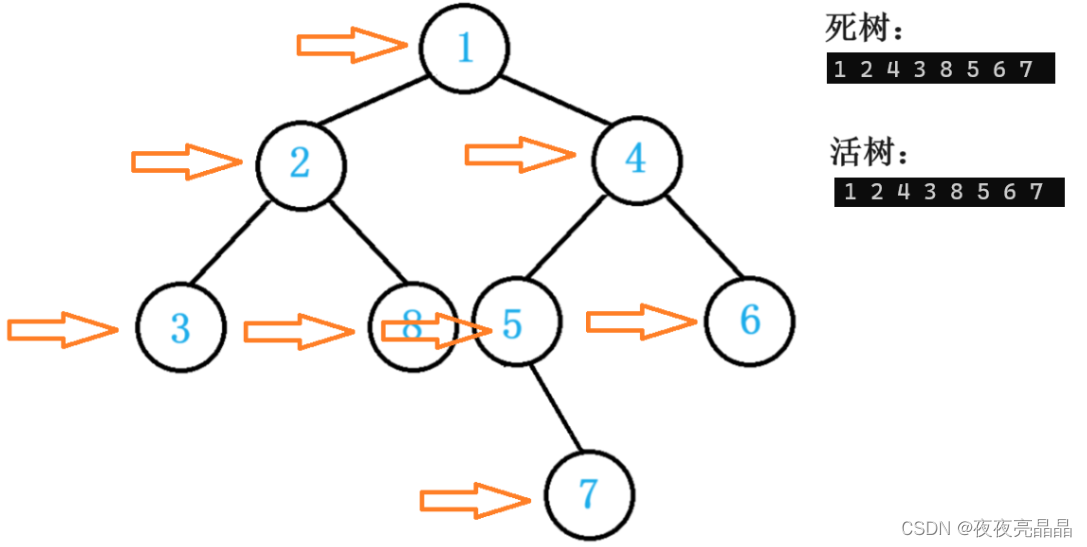
我们来观察一个规律，当每一层的全部结点都被Pop出来时，它的下一次结点已经全部入队列了：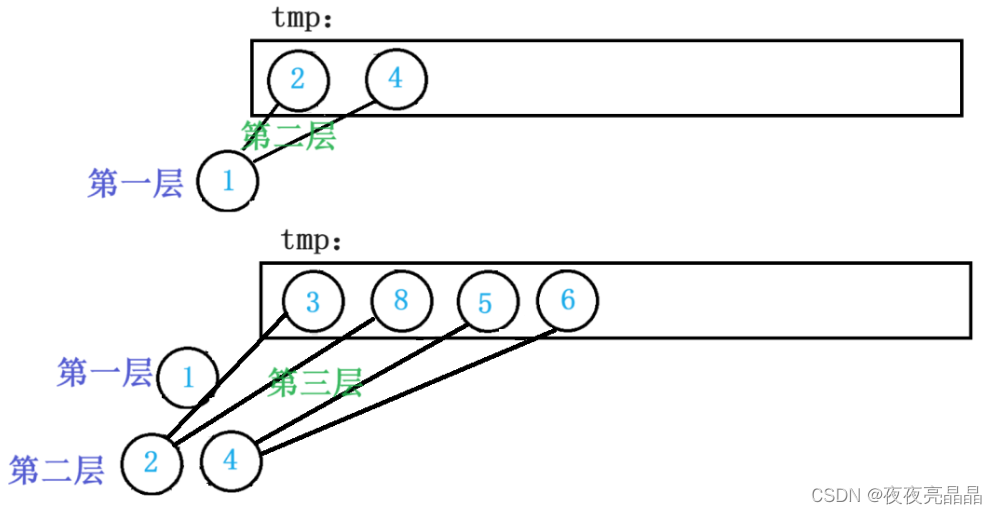

根据这个特点我们就可以每Pop一层后得到下一层的个数，然后继续Pop个数次：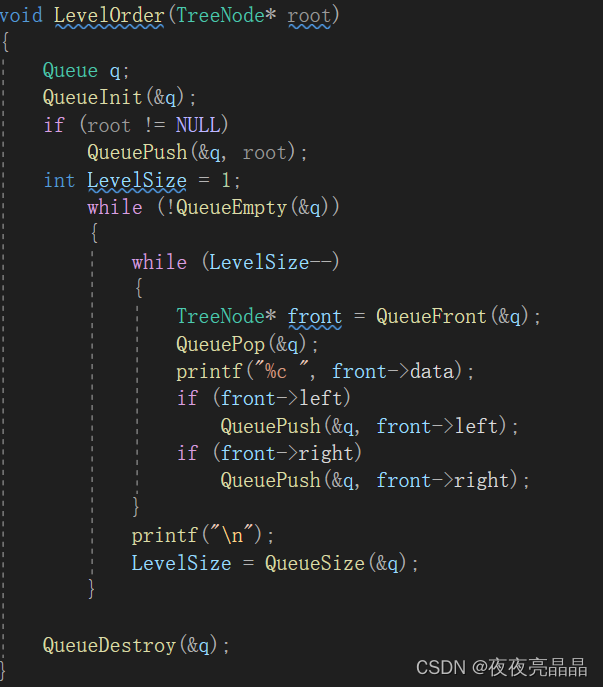
紧接着我们就可以看到我们的打印：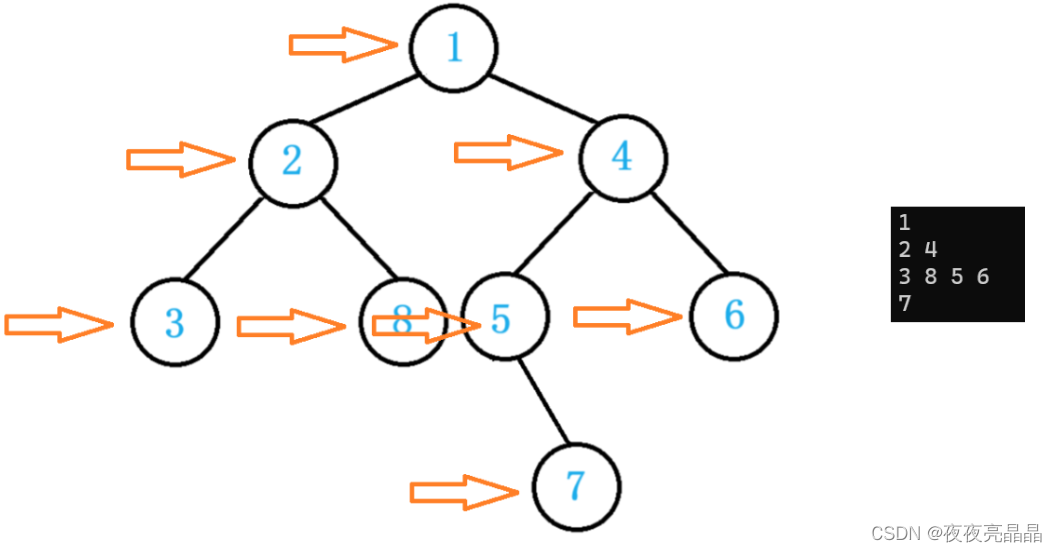

代码：

void LevelOrder(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root != NULL)
		QueuePush(&q, root);
	int LevelSize = 1;
		while (!QueueEmpty(&q))
		{
			while (LevelSize--)
			{
				TreeNode* front = QueueFront(&q);
				QueuePop(&q);
				printf("%c ", front->data);
				if (front->left)
					QueuePush(&q, front->left);
				if (front->right)
					QueuePush(&q, front->right);
			}
			printf("\n");
			LevelSize = QueueSize(&q);
		}
		
	QueueDestroy(&q);
}

十一、检查二叉树是否为完全二叉树

11.1整体思路

如果我们学完层序遍历后，不难发现，如果我们不对二叉树的左右子树做检查，让它们不管空或非空都入队列，当前面队列出空时，若队列中还有元素，则为不完全二叉树：

11.2代码

bool TreeComplete(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	int levelSize = 1;
	while (!QueueEmpty(&q))
	{
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front == NULL)
			break;

		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
	}

	// 前面遇到空以后，后面还有非空就不是完全二叉树
	while (!QueueEmpty(&q))
	{
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(&q);
			return false;
		}
	}

	QueueDestroy(&q);
	return true;
}

完结散花！