编译原理词法分析：NFA转DFA（原理+完整代码+可视化实现）

NFA转换为DFA

【本文内容摘要】

什么是DFA
通过子集构造法将NFA转换为DFA
生成DFA的dot文件并且形成可视化。

如果本文对各位看官有用的话，请记得给一个免费的赞哦（收藏也不错）！

文章目录

NFA转换为DFA
- 一、什么是DFA
- 二、NFA转换为DFA
- - （A）关于如何构造NFA
  - （B）通过子集构造法构建DFA
- 三、可视化DFA
- 四、案例测试
- 五、完整代码（包括了正规式转NFA的部分）

一、什么是DFA

根据百度上的内容。
DFA,即确定有限状态自动机,是编译原理中的一个重要概念。它是一种用于识别正则语言的自动机,也是编译器中词法分析器的核心算法之一。

DFA的工作原理是:从起始状态开始,根据输入符号逐步转移到下一个状态,直到达到终止状态。如果在这个过程中出现了无法转移的情况,那么这个输入符号串就不是这个DFA所能接受的。

那么它和NFA的区别在哪里？

DFA是确定的，也就是说，对于每个状态和每个输入符号，只有一个转移的目标状态。而NFA是不确定的，也就是说，对于某些状态和输入符号，可能有多个或者没有转移的目标状态。
【举个例子】在NFA中，A状态输入a可以转移到B和C两个状态，但是DFA中只能转移到一个状态。
NFA可以有空串转移，也就是说，不需要输入符号就可以从一个状态转移到另一个状态。而DFA不允许有空串转移。
【举个例子】在NFA中，A状态通过空串可以转移到B状态，但是在DFA中，不允许这种空串转移。

二、NFA转换为DFA

NFA转换为DFA的过程，可以用子集构造法来实现。子集构造法的基本思想是，将NFA的状态集合分成若干个子集，每个子集代表一个DFA的状态。子集之间的转移关系，由NFA中的转移关系和空转移决定。具体步骤如下：

计算NFA的初始状态的ε闭包，即包含初始状态和所有通过空转移可以到达的状态的集合。将这个集合作为DFA的初始状态，并标记为未处理。
从未处理的状态集合中选取一个状态（一般是按照顺序），对于每个输入符号，计算该状态经过该符号可以到达的NFA状态的集合，再计算这个集合的ε闭包，得到一个新的状态集合。如果这个集合是新出现的，就将其标记为未处理，否则就是已处理的。根据这个过程，建立DFA的转移关系。
重复第2步，直到没有未处理的状态集合为止。此时，DFA的状态集合和转移关系就构造完成了。
确定DFA的终止状态，即包含NFA的终止状态的状态集合。

（A）关于如何构造NFA

下面的链接中已经详细解释了如何将正规式转换为NFA，这里就不再赘述了。

编译原理词法分析：正则表达式/正规式转NFA（原理+完整代码+可视化实现）

（B）通过子集构造法构建DFA

（1）本文需要用到的结构体

/*构造NFA和DFA所需要的结构体*/
//NFA的节点
struct node
{
	string nodeName;
};

//NFA的边
struct edge
{
	node startName;	//起始点
	node endName;	//目标点
	char tranSymbol;	//转换符号
};


//NFA的组成单元，一个大的NFA单元可以是由很多小单元通过规则拼接起来
struct elem
{
	int edgeCount;	//边数
	edge edgeSet[100];	//该NFA拥有的边
	node startName;	//开始状态
	node endName; //结束状态
};

// 定义 DFA 的状态
struct DFAState {
	set<string> nfaStates;	//一个包含NFA状态的集合
	string stateName;
};

// 定义 DFA 的转换关系
struct DFATransition {
	DFAState fromState;
	DFAState toState;
	char transitionSymbol;
};

node，表示一个NFA的节点，它有一个字符串类型的成员nodeName，表示节点的名称。
edge，表示一个NFA的边，它有三个成员，分别是startName、endName和tranSymbol，分别表示边的起始节点、目标节点和转换符号，其中节点类型是node，转换符号类型是char。
elem，表示一个NFA的组成单元，它有四个成员，分别是edgeCount、edgeSet、startName和endName，分别表示该单元的边数、边集合、开始状态和结束状态，其中边数类型是int，边集合类型是edge的数组，开始状态和结束状态类型是node。
DFAState，表示一个DFA的状态，它有两个成员，分别是nfaStates和stateName，分别表示该状态包含的NFA状态的集合和该状态的名称，其中NFA状态的集合类型是string的集合，状态的名称类型是string。
DFATransition，表示一个DFA的转换关系，它有三个成员，分别是fromState、toState和transitionSymbol，分别表示转换的起始状态、目标状态和符号，其中状态类型是DFAState，符号类型是char。

（2）本文需要用到一些函数（这里留个印象就行）

// 检查 DFA 状态是否在状态集合中,即dfaStates里有没有找到targetState
bool isDFAStateInVector(const vector<DFAState>& dfaStates, const DFAState& targetState) {
    // for 循环遍历 dfaStates 中的每一个状态
    for (const DFAState& state : dfaStates) {
        // 检查当前遍历到的状态的状态名（stateName）是否与目标状态的状态名相等
        if (state.stateName == targetState.stateName) {
            // 如果找到匹配的状态，返回 true
            return true; 
        }
    }
    // 如果遍历完整个状态集合仍未找到匹配的状态，返回 false
    return false; 
}

// 检查转换边是否在边集合中，比如 a->b 是否已经在集合中
bool isTransitionInVector(DFAState dfaState, DFAState dfaNextState, char symbol, vector<DFATransition> dfaTransitions)
{
    // for 循环遍历 dfaTransitions 中的每一条转换边
    for (const DFATransition& transition : dfaTransitions) {
        // 检查当前遍历到的转换边是否与给定的 DFA 状态和符号匹配
        if (transition.fromState.stateName == dfaState.stateName && transition.toState.stateName == dfaNextState.stateName && symbol == transition.transitionSymbol) {
            // 如果找到匹配的转换边，返回 true
            return true;   
        }
    }
    // 如果遍历完整个转换边集合仍未找到匹配的转换边，返回 false
    return false;
}

（3）计算ε闭包（ε-closure）
ε闭包是包含这个集合和所有通过空转移可以到达的状态的集合。简单来说，就是这个状态，通过空串的转移，最终能到达哪些状态（包括它自己）。
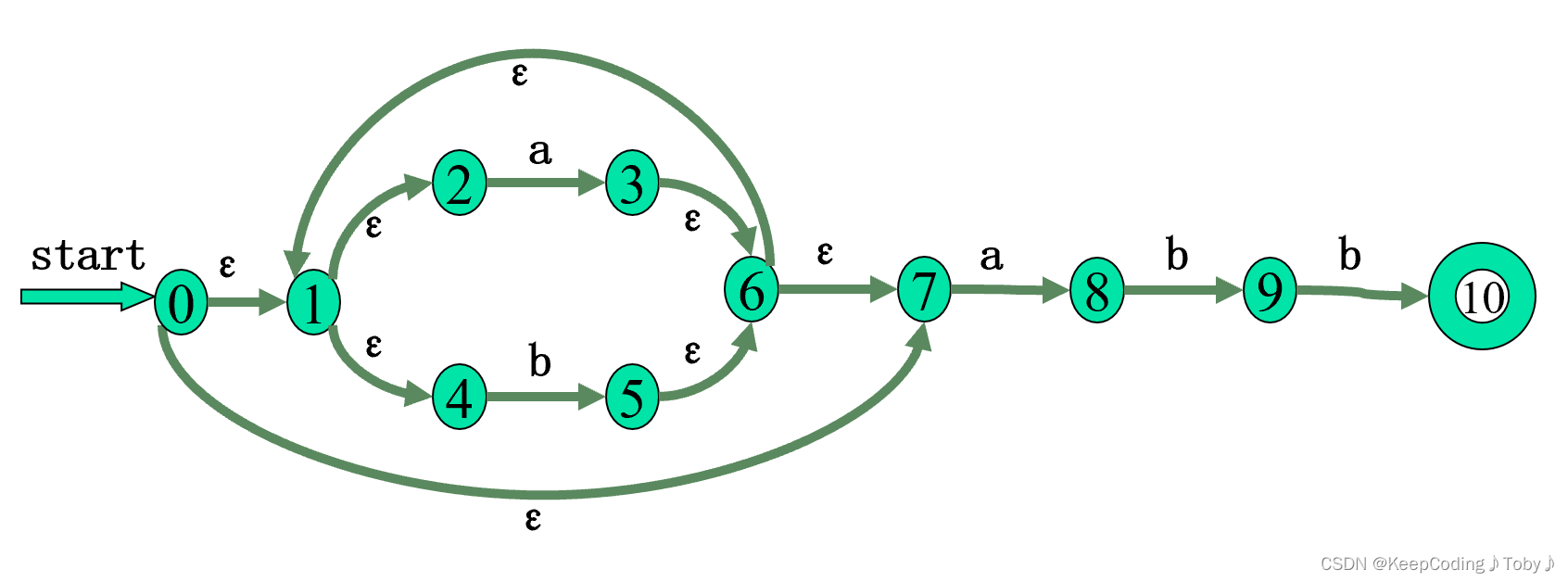
在这里插入图片描述
【举个例子】上图中，0状态通过ε可以转移到1，2，4，7状态，因此ε-closure(0) = {0,1,2,4,7} 。

下面我们来看看代码吧：

// 计算 NFA 状态的ε闭包
DFAState eClosure(const set<string>& nfaStates,elem nfa) {
	DFAState eClosureState;
	eClosureState.nfaStates = nfaStates;

	stack<string> stateStack;

	// 初始化栈，将初始状态加入栈，最开始nfaState里只有NFA_Elem.startName
	for (const string& nfaState_name : nfaStates) {
		stateStack.push(nfaState_name);
	}

	while (!stateStack.empty()) {
		string currentState = stateStack.top();
		stateStack.pop();

		// 遍历 NFA 的边
		for (int i = 0; i < nfa.edgeCount; i++) {
			edge currentEdge = nfa.edgeSet[i];

			// 如果边的起始状态是当前状态，并且边的转换符号是#，那么将目标状态加入ε闭包
			if (currentEdge.startName.nodeName == currentState && currentEdge.tranSymbol == '#') {
				// 检查目标状态是否已经在ε闭包中，避免重复添加
				if (eClosureState.nfaStates.find(currentEdge.endName.nodeName) == eClosureState.nfaStates.end()) {
					eClosureState.nfaStates.insert(currentEdge.endName.nodeName);
					// 将目标状态加入栈以便进一步处理
					stateStack.push(currentEdge.endName.nodeName);
				}
			}
		}
	}

	// 为ε闭包分配一个唯一的名称
	for (const string& nfaState_name : eClosureState.nfaStates) {
		eClosureState.stateName += nfaState_name;
	}

	return eClosureState;
}

它的参数是一个字符串的集合，表示NFA状态的名称，和一个elem结构体，表示一个NFA。它的返回值是一个DFAState结构体，表示这个ε闭包对应的DFA状态。

这段代码的主要逻辑如下：

step1：初始化一个DFAState结构体，将其nfaStates字段设为参数中的字符串集合，表示这个ε闭包包含的NFA状态。将其stateName字段设为空字符串，表示这个ε闭包的名称。
step2：初始化一个栈，将字符串集合中的所有元素压入栈中，表示需要处理的NFA状态。
step3：当栈不为空时，重复以下步骤：

弹出栈顶的元素，记为当前状态，表示正在处理的NFA状态。
遍历NFA的所有边，如果边的起始状态是当前状态，且边的转换符号是#，表示这是一条空转移，那么执行以下步骤：
- 检查边的目标状态是否已经在DFAState的nfaStates字段中，如果不在，就表示这是一个新的NFA状态，需要加入ε闭包中。将其插入DFAState的nfaStates字段中，并将其压入栈中，以便进一步处理。

step4：遍历DFAState的nfaStates字段，将所有元素拼接起来，作为DFAState的stateName字段的值，表示这个ε闭包的名称。返回DFAState结构体。

（3）计算DFA状态的转移
move(T,a)函数代表T状态通过a转移到的所有状态的集合。
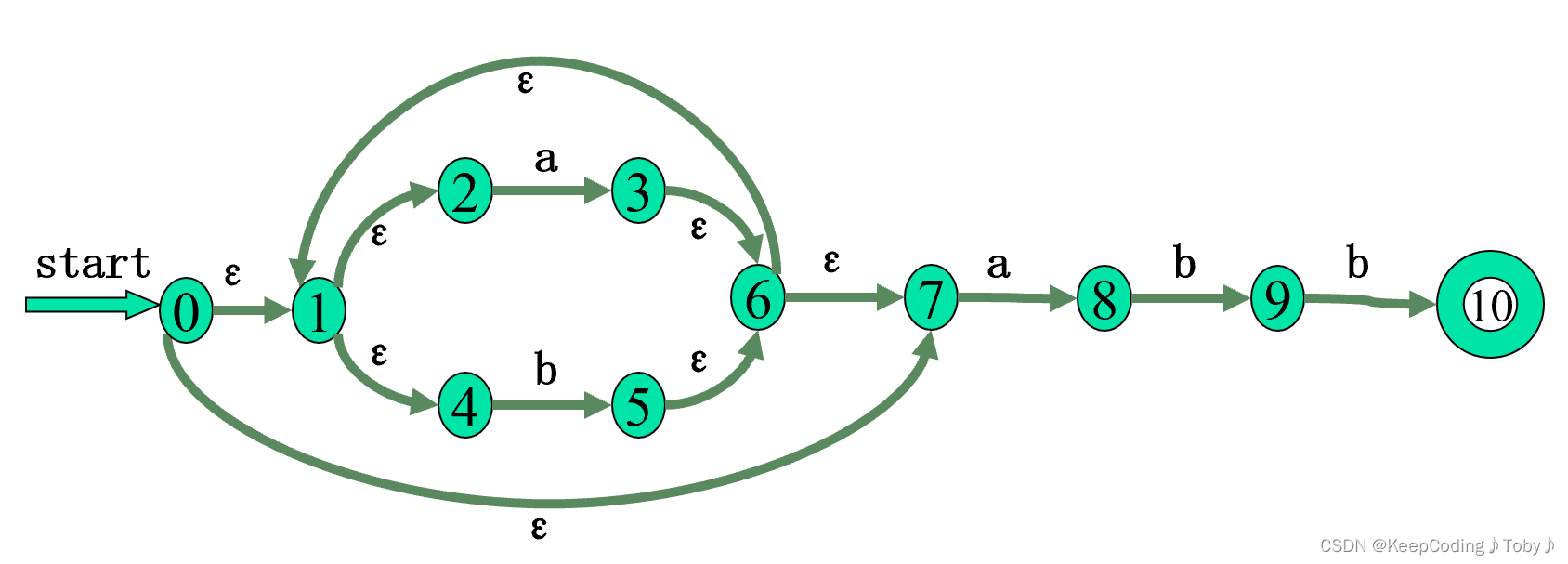
在这里插入图片描述
【举个例子】由T = ε-closure(0) = {0,1,2,4,7}，求move(T,a)：
状态2可以通过a到状态3，状态7可以通过a到状态8，那么，mov(T,a) = {3, 8}。
下面来看代码：

//move函数
DFAState move(const DFAState& dfaState, char transitionSymbol,elem nfa) {
	DFAState nextState;

	// 遍历 DFAState 中的每个 NFA 状态
	for (const string& nfaState_name : dfaState.nfaStates) {
		// 在这里遍历所有 NFA 状态的边
		for (int i = 0; i < nfa.edgeCount; i++) {
			edge currentEdge = nfa.edgeSet[i];

			// 如果边的起始状态是当前状态，且边的转换符号等于输入符号，将目标状态加入 nextState
			if (currentEdge.startName.nodeName == nfaState_name && currentEdge.tranSymbol == transitionSymbol&&currentEdge.tranSymbol!='#') {
				nextState.nfaStates.insert(currentEdge.endName.nodeName);
			}
		}
	}

	// 为 nextState 分配一个唯一的名称
	for (const string& nfaState_name : nextState.nfaStates) {
		nextState.stateName += nfaState_name;
	}

	return nextState;
}

解释：

函数接收当前 DFA 状态（dfaState）、输入符号（transitionSymbol）和一个表示 NFA 的结构体（elem nfa）。
创建一个空的 DFA 状态 nextState 用于存储移动后的状态。
遍历当前 DFA 状态中的每个 NFA 子状态。对于每个 NFA 子状态，遍历 NFA 的边集合，查找符合起始状态和转换符号的边。
如果找到符合条件的边，则将边的目标状态添加到 nextState 的状态集合中。
为了确保状态名称的唯一性，遍历 nextState 的状态集合，并将每个子状态的名称连接起来作为新状态的名称。
返回新的 DFA 状态 nextState。

（4）将NFA转换为DFA
大致过程如下：首先，通过计算NFA初始状态的ε闭包，初始化DFA状态集合。然后，通过迭代遍历DFA状态集合，对每个状态和输入符号进行移动操作，得到下一个状态，并计算其ε闭包。在这个过程中，新的DFA状态和转换关系逐步添加到对应的向量中，确保构建了一个等价于原NFA的DFA。
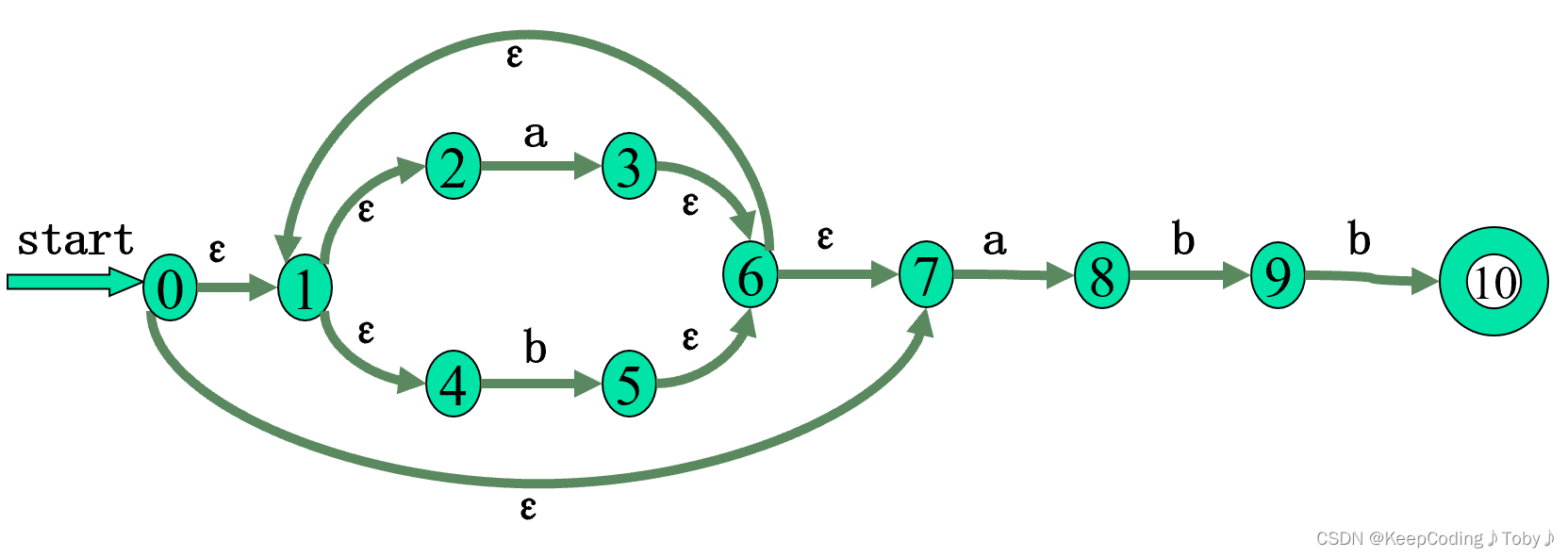
在这里插入图片描述

【举个例子】上图的答案：
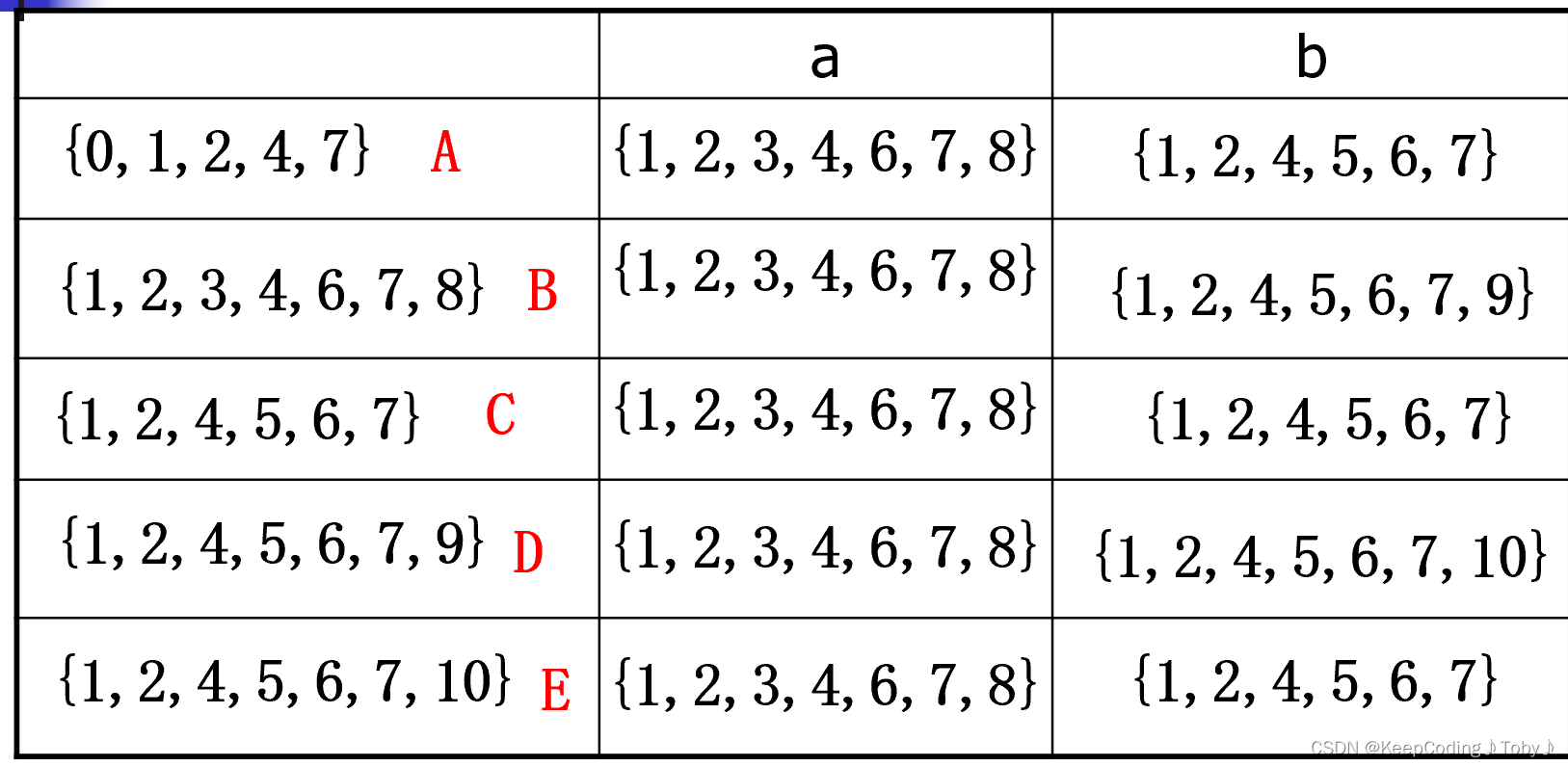
在这里插入图片描述

void buildDFAFromNFA(const elem& NFA_Elem, vector<DFAState>& dfaStates, vector<DFATransition>& dfaTransitions) {
    // 初始化 DFA 状态集合和转换关系
    set<string> nfaInitialStateSet;
    nfaInitialStateSet.insert(NFA_Elem.startName.nodeName);
    DFAState dfaInitialState = eClosure(nfaInitialStateSet, NFA_Elem); // 计算 NFA 初始状态的 ε闭包
    dfaStates.push_back(dfaInitialState);

    // 开始构建 DFA
    for (int i = 0; i < dfaStates.size(); i++) {
        DFAState dfaState = dfaStates[i];
        for (int j = 0; j < NFA_Elem.edgeCount; j++) {
            char symbol = NFA_Elem.edgeSet[j].tranSymbol;
            DFAState nextState = move(dfaState, symbol, NFA_Elem);
            DFAState dfaNextState = eClosure(nextState.nfaStates, NFA_Elem);	//计算move操作后的ε闭包

            if (!nextState.nfaStates.empty()) {
                // 如果下一个状态不为空，且在 DFA 状态集合中还未添加，则加入 DFA 状态集合
                if (!isDFAStateInVector(dfaStates, dfaNextState)) {
                    dfaStates.push_back(dfaNextState);
                }
                // 对于边也要去重，因为等于a的边可能会遍历到两次
                // 如果当前边在 DFA 转换关系中还未添加，则加入 DFA 转换关系
                if (!isTransitionInVector(dfaState, dfaNextState, symbol, dfaTransitions)) {
                    dfaTransitions.push_back({ dfaState, dfaNextState, symbol });
                }
            }
        }
    }
}

代码解释如下：

初始化 DFA 状态集合，包含 NFA 初始状态的ε闭包，并将其加入 DFA 状态集合中。
使用两层循环，外层循环遍历 DFA状态集合，内层循环遍历 NFA 的边集合。

对于每个 DFA 状态和输入符号，通过移动操作得到下一个状态，并计算下一个状态的ε闭包。
如果下一个状态不为空，且在 DFA 状态集合中还未添加，则将其加入 DFA 状态集合。
如果当前边在 DFA转换关系中还未添加，则将其加入 DFA 转换关系。

最终，通过这个过程，构建出完整的 DFA。

三、可视化DFA

原理解释：

函数 generateDotFile_DFA 用于生成描述 DFA（Deterministic Finite Automaton，确定性有限自动机）的 DOT 文件，以便后续使用 Graphviz 等工具可视化显示 DFA 图形。DOT 文件是一种文本格式，描述图的结构、节点和边的关系。

在该函数中，DFA 的状态和转换被映射为 DOT 文件中的节点和边。节点表示状态，边表示状态之间的转移，而边上的标签表示转移所对应的输入符号。

代码：

//生成DFA的dot文件
void generateDotFile_DFA(vector<DFAState>& dfaStates, vector<DFATransition>& dfaTransitions) {
    // 打开名为 "dfa_graph.dot" 的文件流
    std::ofstream dotFile("dfa_graph.dot");

    // 如果文件流成功打开
    if (dotFile.is_open()) {
        // 写入 DOT 文件的头部信息
        dotFile << "digraph DFA {\n";
        dotFile << "  rankdir=LR;  // 横向布局\n\n";
        dotFile << " node [shape = circle];   // 初始状态\n\n";
        dotFile << dfaStates.back().stateName << "[shape = doublecircle];\n";

        // 添加DFA状态
        for (const auto& state : dfaStates) {
            dotFile << "  " << state.stateName;
            dotFile << " [label=\"State " << state.stateName;
            if (state.stateName == dfaStates.front().stateName) dotFile << "\\n(startState)";
            if (state.stateName == dfaStates.back().stateName) { 
                dotFile << "\\n(endState)"; 
            }
            dotFile << "\"];\n";
        }
        dotFile << "\n";

        // 添加DFA转移
        for (const auto& transition : dfaTransitions) {
            dotFile <<"  " <<transition.fromState.stateName << " -> " << transition.toState.stateName << " [label=\"" << transition.transitionSymbol << "\"];\n";
        }

        // 写入 DOT 文件的尾部信息
        dotFile << "}\n";

        // 关闭文件流并输出成功信息
        dotFile.close();
        std::cout << "DFA DOT file generated successfully.\n";
    }
    else {
        // 输出错误信息，表示无法打开 DOT 文件
        std::cerr << "Unable to open DOT file.\n";
    }
}

以下是该函数的详细解释：

文件流初始化： 首先，函数尝试打开名为 “dfa_graph.dot” 的文件以供写入。如果成功打开，则创建一个名为 dotFile 的文件流用于写入DOT文件。
```
std::ofstream dotFile("dfa_graph.dot");
```

文件是否成功打开： 检查文件是否成功打开。如果未成功打开，则输出错误信息并提前结束函数。

if (dotFile.is_open()) {
    // 文件打开成功，继续执行
} else {
    std::cerr << "Unable to open DOT file.\n";
    return;
}

写入DOT文件头部： 写入DOT文件的头部信息，包括指定图的方向为横向布局（LR），以及设置节点的形状为圆形。同时，将终止状态标记为双圈。

dotFile << "digraph DFA {\n";
dotFile << "  rankdir=LR;  // 横向布局\n\n";
dotFile << " node [shape = circle];   // 初始状态\n\n";
dotFile << dfaStates.back().stateName << "[shape = doublecircle];\n";

添加DFA状态： 遍历DFA状态集合，为每个状态添加一个DOT文件中的节点，包括状态名称和标签。如果是起始状态，则附加 “(startState)” 标签，如果是终止状态，则附加 “(endState)” 标签。

for (const auto& state : dfaStates) {
    dotFile << "  " << state.stateName;
    dotFile << " [label=\"State " << state.stateName;
    if (state.stateName == dfaStates.front().stateName) dotFile << "\\n(startState)";
    if (state.stateName == dfaStates.back().stateName) { 
        dotFile << "\\n(endState)"; 
    }
    dotFile << "\"];\n";
}

添加DFA转移： 遍历DFA转换集合，为每个转换添加一个DOT文件中的边，标注起始状态、目标状态和转换符号。

for (const auto& transition : dfaTransitions) {
    dotFile <<"  " <<transition.fromState.stateName << " -> " << transition.toState.stateName << " [label=\"" << transition.transitionSymbol << "\"];\n";
}

写入DOT文件尾部： 写入DOT文件的尾部信息，表示图的结束。
```
dotFile << "}\n";
```
文件流关闭： 关闭文件流，确保文件操作完成。
```
dotFile.close();
```
输出信息： 如果所有操作都成功完成，则输出生成DOT文件成功的信息，否则输出无法打开文件的错误信息。
```
std::cout << "DFA DOT file generated successfully.\n";
```

这样，函数完成了将DFA的结构转换为DOT文件的过程，以便进一步的图形可视化。

四、案例测试

1、(a|b|c)*
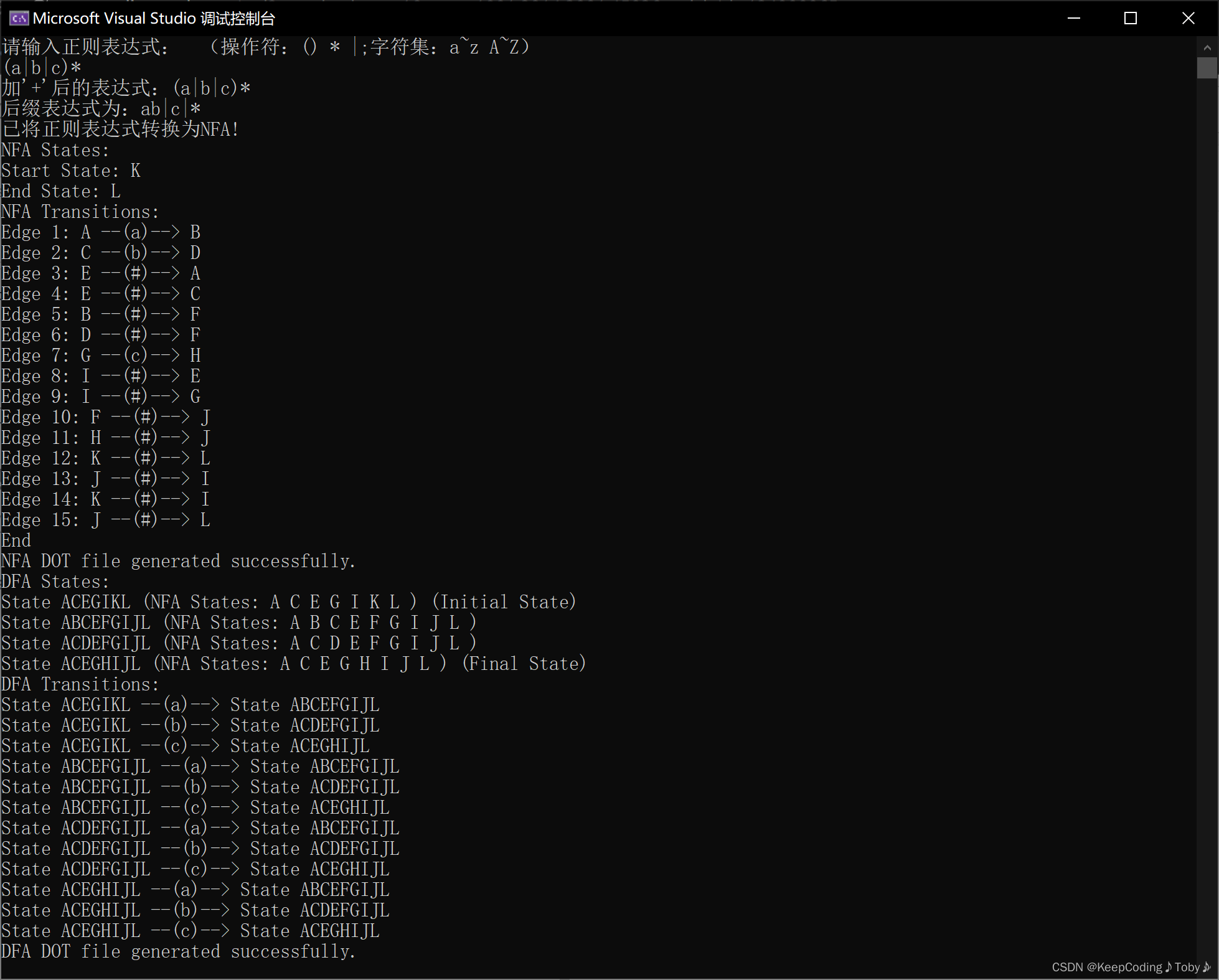
在这里插入图片描述
上图为visual studio中的运行结果。
下面打开文件夹以及命令提示符，将dot文件可视化

NFA图片：
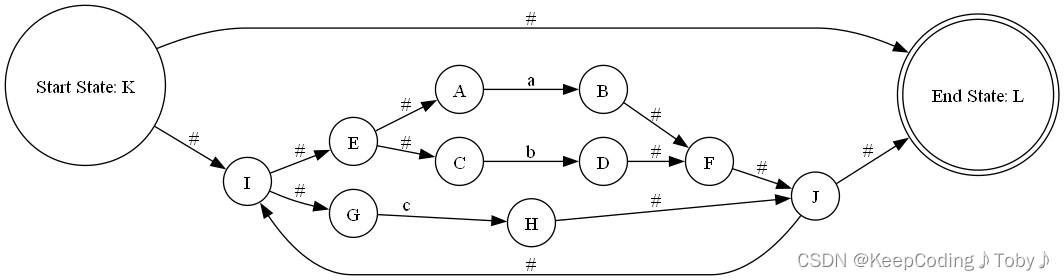
在这里插入图片描述
DFA图片：

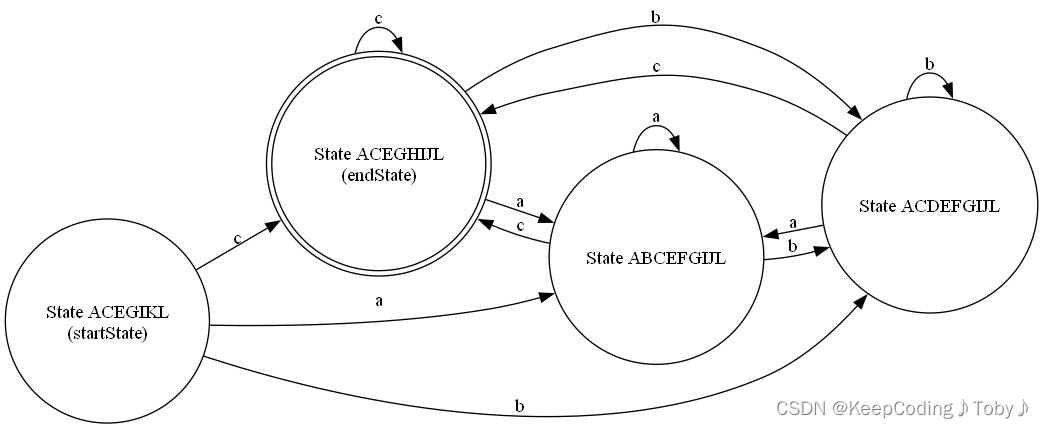
2、a(b|c)^*de
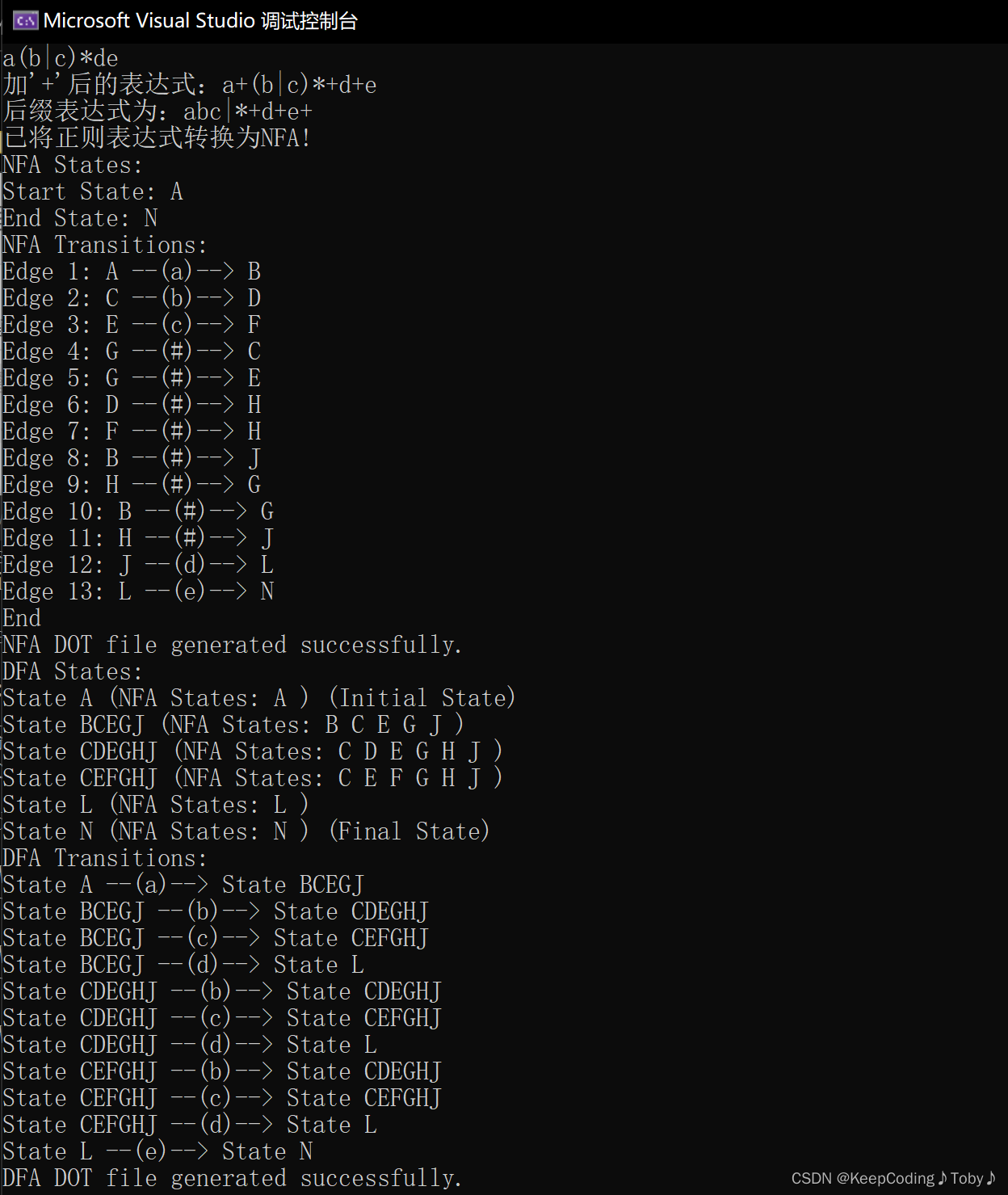
在这里插入图片描述
NFA:

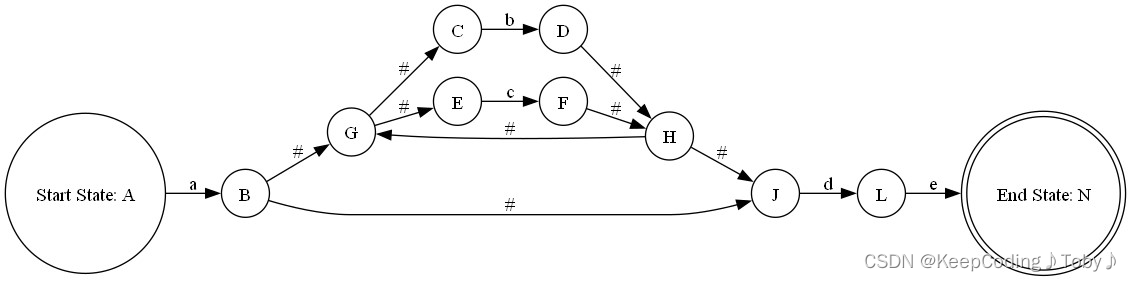
DFA:
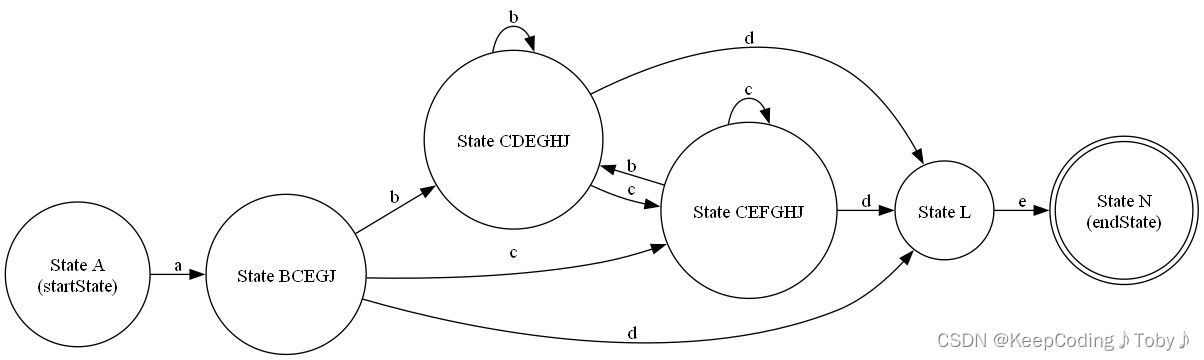
在这里插入图片描述

五、完整代码（包括了正规式转NFA的部分）

//head.h
#ifndef HEAD_H
#define HEAD_H

#include <iostream>
#include <stdio.h>
#include <cctype>
#include <stack>
#include <string>
#include <map>
#include <set>
#include <vector>
#include<iterator>
#include <fstream>

using namespace std;

/*构造NFA和DFA所需要的结构体*/
//NFA的节点
struct node
{
	string nodeName;
};

//NFA的边
struct edge
{
	node startName;	//起始点
	node endName;	//目标点
	char tranSymbol;	//转换符号
};


//NFA的组成单元，一个大的NFA单元可以是由很多小单元通过规则拼接起来
struct elem
{
	int edgeCount;	//边数
	edge edgeSet[100];	//该NFA拥有的边
	node startName;	//开始状态
	node endName; //结束状态
};

// 定义 DFA 的状态
struct DFAState {
	set<string> nfaStates;	//一个包含NFA状态的集合
	string stateName;
};

// 定义 DFA 的转换关系
struct DFATransition {
	DFAState fromState;
	DFAState toState;
	char transitionSymbol;
};

/*下面是转换为DFA的主要函数*/

// 计算 NFA 状态的ε闭包
DFAState eClosure(const set<string>& nfaStates, elem nfa);

// 计算 DFA 的状态转移
DFAState move(const DFAState& dfaState, char transitionSymbol,elem nfa);

// 检查 DFA 状态是否在状态集合中
bool isDFAStateInVector(const vector<DFAState>& dfaStates, const DFAState& targetState);

//检查转换边是否在边集合中，比如a->b是否已经在集合中
bool isTransitionInVector(DFAState, DFAState, char,vector<DFATransition>);

//NFA转换为DFA
void buildDFAFromNFA(const elem& NFA_Elem, vector<DFAState>& dfaStates, vector<DFATransition>& dfaTransitions);

// 显示 DFA 状态和转移关系
void displayDFA(const vector<DFAState>& dfaStates, const vector<DFATransition>& dfaTransitions);

//生成dot文件
void generateDotFile_DFA(vector<DFAState>& dfaStates, vector<DFATransition>& dfaTransitions);


/*下面是构造NFA的主要函数*/
//创建新节点
node new_node();

//处理 a
elem act_Elem(char);

//处理a|b
elem act_Unit(elem, elem);

//组成单元拷贝函数
void elem_copy(elem&, elem);

//处理ab
elem act_join(elem, elem);

//处理 a*
elem act_star(elem);

void input(string&);

string add_join_symbol(string);	//两个单元拼接在一起相当于中间有一个+，如ab相当于a+b

class infixToPostfix {
public:
	infixToPostfix(const string& infix_expression);

	int is_letter(char check);
	int ispFunc(char c);
	int icpFunc(char c);
	void infToPost();
	string getResult();

private:
	string infix;
	string postfix;
	map<char, int> isp;
	map<char, int> icp;
};

elem express_to_NFA(string);

void Display(elem);

int is_letter(char check);

void generateDotFile_NFA(const elem& nfa);
#endif

//func.cpp
#include "head.h"

int nodeNum = 0;

/*下面是转换为DFA的主要函数*/

// 计算 NFA 状态的ε闭包
DFAState eClosure(const set<string>& nfaStates,elem nfa) {
	DFAState eClosureState;
	eClosureState.nfaStates = nfaStates;

	stack<string> stateStack;

	// 初始化栈，将初始状态加入栈，最开始nfaState里只有NFA_Elem.startName
	for (const string& nfaState_name : nfaStates) {
		stateStack.push(nfaState_name);
	}

	while (!stateStack.empty()) {
		string currentState = stateStack.top();
		stateStack.pop();

		// 遍历 NFA 的边
		for (int i = 0; i < nfa.edgeCount; i++) {
			edge currentEdge = nfa.edgeSet[i];

			// 如果边的起始状态是当前状态，并且边的转换符号是#，那么将目标状态加入ε闭包
			if (currentEdge.startName.nodeName == currentState && currentEdge.tranSymbol == '#') {
				// 检查目标状态是否已经在ε闭包中，避免重复添加
				if (eClosureState.nfaStates.find(currentEdge.endName.nodeName) == eClosureState.nfaStates.end()) {
					eClosureState.nfaStates.insert(currentEdge.endName.nodeName);
					// 将目标状态加入栈以便进一步处理
					stateStack.push(currentEdge.endName.nodeName);
				}
			}
		}
	}

	// 为ε闭包分配一个唯一的名称
	for (const string& nfaState_name : eClosureState.nfaStates) {
		eClosureState.stateName += nfaState_name;
	}

	return eClosureState;
}

//move函数
DFAState move(const DFAState& dfaState, char transitionSymbol,elem nfa) {
	DFAState nextState;

	// 遍历 DFAState 中的每个 NFA 状态
	for (const string& nfaState_name : dfaState.nfaStates) {
		// 在这里遍历所有 NFA 状态的边
		for (int i = 0; i < nfa.edgeCount; i++) {
			edge currentEdge = nfa.edgeSet[i];

			// 如果边的起始状态是当前状态，且边的转换符号等于输入符号，将目标状态加入 nextState
			if (currentEdge.startName.nodeName == nfaState_name && currentEdge.tranSymbol == transitionSymbol&&currentEdge.tranSymbol!='#') {
				nextState.nfaStates.insert(currentEdge.endName.nodeName);
			}
		}
	}

	// 为 nextState 分配一个唯一的名称
	for (const string& nfaState_name : nextState.nfaStates) {
		nextState.stateName += nfaState_name;
	}

	return nextState;
}

// 检查 DFA 状态是否在状态集合中,即dfaStates里有没有找到targetState
bool isDFAStateInVector(const vector<DFAState>& dfaStates, const DFAState& targetState) {
	for (const DFAState& state : dfaStates) {
		if (state.stateName == targetState.stateName) {
			return true; // 找到匹配的状态
		}
	}
	return false; // 没有找到匹配的状态
}

//检查转换边是否在边集合中，比如a->b是否已经在集合中
bool isTransitionInVector(DFAState dfaState, DFAState dfaNextState, char symbol,vector<DFATransition> dfaTransitions)
{
	for (const DFATransition& transition : dfaTransitions) {
		if (transition.fromState.stateName == dfaState.stateName && dfaNextState.stateName == dfaNextState.stateName&&symbol==transition.transitionSymbol) {
			return true;	//找到匹配的状态
		}
	}
	return false;
}

void buildDFAFromNFA(const elem& NFA_Elem, vector<DFAState>& dfaStates, vector<DFATransition>& dfaTransitions) {
	// 初始化 DFA 状态集合和转换关系
	set<string> nfaInitialStateSet;
	nfaInitialStateSet.insert(NFA_Elem.startName.nodeName);
	DFAState dfaInitialState = eClosure(nfaInitialStateSet, NFA_Elem); // 计算 NFA 初始状态的 ε闭包
	dfaStates.push_back(dfaInitialState);

	// 开始构建 DFA
	for (int i = 0; i < dfaStates.size(); i++) {
		DFAState dfaState = dfaStates[i];
		for (int j = 0; j < NFA_Elem.edgeCount; j++) {
			char symbol = NFA_Elem.edgeSet[j].tranSymbol;
			DFAState nextState = move(dfaState, symbol, NFA_Elem);
			DFAState dfaNextState = eClosure(nextState.nfaStates, NFA_Elem);

			if (!nextState.nfaStates.empty()) {
				// 如果下一个状态不为空，且在 DFA 状态集合中还未添加，则加入 DFA 状态集合
				if (!isDFAStateInVector(dfaStates, dfaNextState)) {
					dfaStates.push_back(dfaNextState);
				}
				// 对于边也要去重，因为等于a的边可能会遍历到两次
				// 如果当前边在 DFA 转换关系中还未添加，则加入 DFA 转换关系
				if (!isTransitionInVector(dfaState, dfaNextState, symbol, dfaTransitions)) {
					dfaTransitions.push_back({ dfaState, dfaNextState, symbol });
				}
			}
		}
	}
}

// 显示 DFA 状态和转移关系，包括起始和结束状态
void displayDFA(const vector<DFAState>& dfaStates, const vector<DFATransition>& dfaTransitions) {
	cout << "DFA States:" << endl;

	for (const DFAState& state : dfaStates) {
		cout << "State " << state.stateName << " (NFA States: ";
		for (const string& nfaState_name : state.nfaStates) {
			cout << nfaState_name << " ";
		}
		cout << ")";
		if (state.stateName == dfaStates.front().stateName) {
			cout << " (Initial State)";
		}
		if (state.stateName == dfaStates.back().stateName) {
			cout << " (Final State)";
		}
		cout << endl;
	}

	cout << "DFA Transitions:" << endl;
	for (const DFATransition& transition : dfaTransitions) {
		cout << "State " << transition.fromState.stateName << " --(" << transition.transitionSymbol << ")--> State " << transition.toState.stateName << endl;
	}
}

//生成DFA的dot文件
void generateDotFile_DFA(vector<DFAState>& dfaStates, vector<DFATransition>& dfaTransitions) {
	std::ofstream dotFile("dfa_graph.dot");

	if (dotFile.is_open()) {
		dotFile << "digraph DFA {\n";
		dotFile << "  rankdir=LR;  // 横向布局\n\n";
		dotFile << " node [shape = circle];   // 初始状态\n\n";
		dotFile << dfaStates.back().stateName << "[shape = doublecircle];\n";
		// 添加DFA状态
		for (const auto& state : dfaStates) {
			dotFile << "  " << state.stateName;
			dotFile << " [label=\"State " << state.stateName;
			if (state.stateName == dfaStates.front().stateName) dotFile << "\\n(startState)";
			if (state.stateName == dfaStates.back().stateName) { 
				dotFile << "\\n(endState)"; 
			}
			dotFile << "\"];\n";
		}
		dotFile << "\n";

		// 添加DFA转移
		for (const auto& transition : dfaTransitions) {
			dotFile <<"  " <<transition.fromState.stateName << " -> " << transition.toState.stateName << " [label=\"" << transition.transitionSymbol << "\"];\n";
		}

		dotFile << "}\n";

		dotFile.close();
		std::cout << "DFA DOT file generated successfully.\n";
	}
	else {
		std::cerr << "Unable to open DOT file.\n";
	}
}

/*下面是构造NFA的主要函数*/

//创建新节点
node new_node()
{
	node newNode;
	newNode.nodeName = nodeNum + 65;//将名字用大写字母表示
	nodeNum++;
	return newNode;
}

//接收输入正规表达式
void input(string& RE)
{
	cout << "请输入正则表达式：  （操作符：() * |;字符集：a~z A~Z）" << endl;
	cin >> RE;
}


//组成单元拷贝函数
void elem_copy(elem& dest, elem source)
{
	for (int i = 0; i < source.edgeCount; i++) {
		dest.edgeSet[dest.edgeCount + i] = source.edgeSet[i];
	}
	dest.edgeCount += source.edgeCount;
}

//处理 a
elem act_Elem(char c)
{
	//新节点
	node startNode = new_node();
	node endNode = new_node();

	//新边
	edge newEdge;
	newEdge.startName = startNode;
	newEdge.endName = endNode;
	newEdge.tranSymbol = c;

	//新NFA组成元素（小的NFA元素/单元)
	elem newElem;
	newElem.edgeCount = 0;	//初始状态
	newElem.edgeSet[newElem.edgeCount++] = newEdge;
	newElem.startName = newElem.edgeSet[0].startName;
	newElem.endName = newElem.edgeSet[0].endName;

	return newElem;
}

//处理a|b
elem act_Unit(elem fir, elem sec)
{
	elem newElem;
	newElem.edgeCount = 0;
	edge edge1, edge2, edge3, edge4;

	//获得新的状态节点
	node startNode = new_node();
	node endNode = new_node();

	//构建e1（连接起点和AB的起始点A）
	edge1.startName = startNode;
	edge1.endName = fir.startName;
	edge1.tranSymbol = '#';

	//构建e2（连接起点和CD的起始点C）
	edge2.startName = startNode;
	edge2.endName = sec.startName;
	edge2.tranSymbol = '#';

	//构建e3（连接AB的终点和终点）
	edge3.startName = fir.endName;
	edge3.endName = endNode;
	edge3.tranSymbol = '#';

	//构建e4（连接CD的终点和终点）
	edge4.startName = sec.endName;
	edge4.endName = endNode;
	edge4.tranSymbol = '#';

	//将fir和sec合并
	elem_copy(newElem, fir);
	elem_copy(newElem, sec);

	//新构建的4条边
	newElem.edgeSet[newElem.edgeCount++] = edge1;
	newElem.edgeSet[newElem.edgeCount++] = edge2;
	newElem.edgeSet[newElem.edgeCount++] = edge3;
	newElem.edgeSet[newElem.edgeCount++] = edge4;

	newElem.startName = startNode;
	newElem.endName = endNode;

	return newElem;
}

//处理 N(s)N(t)
elem act_join(elem fir, elem sec)
{
	//将fir的结束状态和sec的开始状态合并，将sec的边复制给fir，将fir返回
	//将sec中所有以StartState开头的边全部修改
	for (int i = 0; i < sec.edgeCount; i++) {
		if (sec.edgeSet[i].startName.nodeName.compare(sec.startName.nodeName) == 0)
		{
			sec.edgeSet[i].startName = fir.endName; //该边e1的开始状态就是N(t)的起始状态
		}
		else if (sec.edgeSet[i].endName.nodeName.compare(sec.startName.nodeName) == 0) {
			sec.edgeSet[i].endName = fir.endName; //该边e2的结束状态就是N(t)的起始状态
		}
	}
	sec.startName = fir.endName;

	elem_copy(fir, sec);

	//将fir的结束状态更新为sec的结束状态
	fir.endName = sec.endName;
	return fir;
}

//处理a*
elem act_star(elem Elem)
{
	elem newElem;
	newElem.edgeCount = 0;
	edge edge1, edge2, edge3, edge4;

	//获得新状态节点
	node startNode = new_node();
	node endNode = new_node();

	//e1
	edge1.startName = startNode;
	edge1.endName = endNode;
	edge1.tranSymbol = '#';	//闭包取空串

	//e2
	edge2.startName = Elem.endName;
	edge2.endName = Elem.startName;
	edge2.tranSymbol = '#';

	//e3
	edge3.startName = startNode;
	edge3.endName = Elem.startName;
	edge3.tranSymbol = '#';

	//e4
	edge4.startName = Elem.endName;
	edge4.endName = endNode;
	edge4.tranSymbol = '#';

	//构建单元
	elem_copy(newElem, Elem);

	//将新构建的四条边加入EdgeSet
	newElem.edgeSet[newElem.edgeCount++] = edge1;
	newElem.edgeSet[newElem.edgeCount++] = edge2;
	newElem.edgeSet[newElem.edgeCount++] = edge3;
	newElem.edgeSet[newElem.edgeCount++] = edge4;

	//构建NewElem的启示状态和结束状态
	newElem.startName = startNode;
	newElem.endName = endNode;

	return newElem;
}

int is_letter(char check) {
	if (check >= 'a' && check <= 'z' || check >= 'A' && check <= 'Z')
		return true;
	return false;
}
//
string add_join_symbol(string add_string)
{
	int length = add_string.size();
	int return_string_length = 0;
	char* return_string = new char[2 * length + 2];//最多是两倍
	char first, second;
	for (int i = 0; i < length - 1; i++)
	{
		first = add_string.at(i);
		second = add_string.at(i + 1);
		return_string[return_string_length++] = first;
		//要加的可能性如ab 、 *b 、 a( 、 )b 等情况
		//若第二个是字母、第一个不是'('、'|'都要添加
		if (first != '(' && first != '|' && is_letter(second))
		{
			return_string[return_string_length++] = '+';
		}
		//若第二个是'(',第一个不是'|'、'(',也要加
		else if (second == '(' && first != '|' && first != '(')
		{
			return_string[return_string_length++] = '+';
		}
	}
	//将最后一个字符写入second
	return_string[return_string_length++] = second;
	return_string[return_string_length] = '\0';
	string STRING(return_string);
	cout << "加'+'后的表达式：" << STRING << endl;
	return STRING;
}

//类里的各类元素定义
infixToPostfix::infixToPostfix(const string& infix_expression) : infix(infix_expression), postfix("") {
	isp = { {'+', 3}, {'|', 5}, {'*', 7},  {'(', 1}, {')', 8}, {'#', 0} };
	icp = { {'+', 2}, {'|', 4}, {'*', 6}, {'(', 8}, {')', 1}, {'#', 0} };
}

int infixToPostfix::is_letter(char check) {
	if (check >= 'a' && check <= 'z' || check >= 'A' && check <= 'Z')
		return true;
	return false;
}

int infixToPostfix::ispFunc(char c) {
	int priority = isp.count(c) ? isp[c] : -1;
	if (priority == -1) {
		cerr << "error: 出现未知符号！" << endl;
		exit(1);  // 异常退出
	}
	return priority;
}

int infixToPostfix::icpFunc(char c) {
	int priority = icp.count(c) ? icp[c] : -1;
	if (priority == -1) {
		cerr << "error: 出现未知符号！" << endl;
		exit(1);  // 异常退出
	}
	return priority;
}

void infixToPostfix::infToPost() {
	string infixWithHash = infix + "#";
	stack<char> stack;
	int loc = 0;
	while (!stack.empty() || loc < infixWithHash.size()) {
		if (is_letter(infixWithHash[loc])) {
			postfix += infixWithHash[loc];
			loc++;
		}
		else {
			char c1 = (stack.empty()) ? '#' : stack.top();
			char c2 = infixWithHash[loc];
			if (ispFunc(c1) < icpFunc(c2)) {
				stack.push(c2);
				loc++;
			}
			else if (ispFunc(c1) > icpFunc(c2)) {
				postfix += c1;
				stack.pop();
			}
			else {
				if (c1 == '#' && c2 == '#') {
					break;
				}
				stack.pop();
				loc++;
			}
		}
	}
}

string infixToPostfix::getResult() {
	postfix = ""; // 清空结果
	infToPost();
	return postfix;
}

/**表达式转NFA处理函数,返回最终的NFA集合
*/
elem express_to_NFA(string expression)
{
	int length = expression.size();
	char element;
	elem Elem, fir, sec;
	stack<elem> STACK;
	for (int i = 0; i < length; i++)
	{
		element = expression.at(i);
		switch (element)
		{
		case '|':
			sec = STACK.top();
			STACK.pop();
			fir = STACK.top();
			STACK.pop();
			Elem = act_Unit(fir, sec);
			STACK.push(Elem);
			break;
		case '*':
			fir = STACK.top();
			STACK.pop();
			Elem = act_star(fir);
			STACK.push(Elem);
			break;
		case '+':
			sec = STACK.top();
			STACK.pop();
			fir = STACK.top();
			STACK.pop();
			Elem = act_join(fir, sec);
			STACK.push(Elem);
			break;
		default:
			Elem = act_Elem(element);
			STACK.push(Elem);
		}
	}
	cout << "已将正则表达式转换为NFA!" << endl;
	Elem = STACK.top();
	STACK.pop();

	return Elem;
}

//打印NFA
void Display( elem Elem) {
	cout << "NFA States:" << endl;
	cout << "Start State: " << Elem.startName.nodeName << endl;
	cout << "End State: " << Elem.endName.nodeName << endl;

	cout << "NFA Transitions:" << endl;
	for (int i = 0; i < Elem.edgeCount; i++) {
		cout << "Edge " << i + 1 << ": ";
		cout << Elem.edgeSet[i].startName.nodeName << " --(" << Elem.edgeSet[i].tranSymbol << ")--> ";
		cout << Elem.edgeSet[i].endName.nodeName << endl;
	}

	cout << "End" << endl;
}

//生成NFAdot文件
void generateDotFile_NFA(const elem& nfa) {
	std::ofstream dotFile("nfa_graph.dot");

	if (dotFile.is_open()) {
		dotFile << "digraph NFA {\n";
		dotFile << "  rankdir=LR;  // 横向布局\n\n";
		dotFile << " node [shape = circle];   // 状态节点\n\n";

		dotFile << nfa.endName.nodeName << " [shape=doublecircle];\n";
		// 添加 NFA 状态
		dotFile << "  " << nfa.startName.nodeName << " [label=\"Start State: " << nfa.startName.nodeName << "\"];\n";
		dotFile << "  " << nfa.endName.nodeName << " [label=\"End State: " << nfa.endName.nodeName << "\"];\n";

		// 添加 NFA 转移
		for (int i = 0; i < nfa.edgeCount; i++) {
			const edge& currentEdge = nfa.edgeSet[i];
			dotFile << "  " << currentEdge.startName.nodeName << " -> " << currentEdge.endName.nodeName << " [label=\"" << currentEdge.tranSymbol << "\"];\n";
		}

		dotFile << "}\n";

		dotFile.close();
		std::cout << "NFA DOT file generated successfully.\n";
	}
	else {
		std::cerr << "Unable to open NFA DOT file.\n";
	}
}

//main.cpp
#include "head.h" // 包含提供的头文件

int main() {
    string Regular_Expression;
    elem NFA_Elem;
    input(Regular_Expression);
    if (Regular_Expression.length() > 1)    Regular_Expression = add_join_symbol(Regular_Expression);
    infixToPostfix Solution(Regular_Expression);
    //中缀转后缀
    cout << "后缀表达式为：";
    Regular_Expression = Solution.getResult();
    cout << Regular_Expression << endl;
    //表达式转NFA
    NFA_Elem = express_to_NFA(Regular_Expression);
    //显示
    Display(NFA_Elem);
    //生成NFAdot文件
    generateDotFile_NFA(NFA_Elem);

    // 初始化 DFA 状态集合和转换关系
    vector<DFAState> dfaStates; //用于存储所有的DFA状态
    vector<DFATransition> dfaTransitions; //用于存储DFA状态之间的转移
    set<string> nfaInitialStateSet;   //存储NFA的初始状态
    buildDFAFromNFA(NFA_Elem, dfaStates, dfaTransitions);//从NFA构造DFA
    // 显示 DFA
    displayDFA(dfaStates, dfaTransitions);

    //生成DFAdot文件
    generateDotFile_DFA(dfaStates,dfaTransitions);
    return 0;
}