回归分析:预测和建模
- 写在开头
- 1. 回归分析的基本概念
- 2. 回归分析的方法
-
- 2.1 简单线性回归
-
- 2.1.1 数学知识
- 2.1.2 应用举例
- 2.2 多元线性回归
-
- 2.2.1 数学公式和应用
- 2.2.1 应用场景举例
- 2.3 多项式回归
-
- 2.3.1 数学公式和应用
- 2.3.2 应用场景举例
- 2.4 逻辑回归
-
- 2.4.1 数学公式和应用
- 2.4.2 应用场景举例
- 3.模型评估
-
- 3.1 均方误差(Mean Squared Error,MSE):
- 3.2 均方根误差(RMSE):
- 3.3 决定系数(Coefficient of Determination,R²)
- 3.4 平均绝对误差(Mean Absolute Error,MAE)
- 3.5 拟合优度(Goodness of Fit)
- 3.6 交叉验证
- 写在最后
写在开头
回归分析是数据科学中一项不可或缺的工具,为我们提供了洞察变量之间关系的能力,使我们能够更准确地预测未来趋势并进行有力的建模。在本篇博客中,我们将深入探讨回归分析的核心概念和方法,通过具体场景、实例代码以及深刻的统计学知识,助力读者在预测与建模的复杂领域中游刃有余。
1. 回归分析的基本概念
回归分析旨在探讨一个或多个自变量与因变量之间的关系。其中,自变量是影响因变量的因素,而因变量是我们希望预测或解释的变量。简而言之,回归分析可以帮助我们了解变量之间的相互作用,并用这些关系进行预测。
2. 回归分析的方法
下面是回归分析的一些对比和介绍,可以帮助你更好的理解回归分析。
| 回归类型 | 优点 | 缺点 | 适用范围 | 注意事项 | 应用场景举例 |
|---|---|---|---|---|---|
| 简单线性回归 | - 易于理解和实现。 | - 仅适用于线性关系。 | - 适用于仅包含一个自变量和一个因变量的简单关系。 | - 确保数据符合线性假设。 | - 广告费用与销售额之间的关系。 |
| 多元线性回归 | - 考虑多个自变量,能够更准确地建模真实世界复杂关系。 | - 对多重共线性敏感。 | - 适用于多个自变量与一个因变量之间的复杂关系。 | - 检测和处理多重共线性。 | - 房价与面积、卧室数量、浴室数量等因素的关系。 |
| 多项式回归 | - 能够拟合非线性关系。 | - 对高阶多项式的拟合可能过度复杂,容易过拟合。 | - 适用于数据呈现非线性关系,但避免使用过高阶多项式。 | - 谨慎选择多项式的阶数,避免过拟合。 | - 温度与销售额之间可能存在非线性关系。 |
| 逻辑回归 | - 用于二分类问题,输出结果可解释为概率。 | - 对多类别问题不直接适用。 | - 适用于二分类问题,如是/否、成功/失败等。 | - 确保样本均衡,避免过拟合。 | - 产品是否被购买的预测,疾病是否发病的概率预测。 |
在选择回归分析方法时,需要综合考虑数据的性质、问题的复杂程度以及模型的可解释性。不同类型的回归方法各有优劣,合适的方法应根据具体情况进行选择。注意事项的遵循可以提高建模的准确性和可靠性,确保模型的实际应用效果更好.
2.1 简单线性回归
简单线性回归是一种统计分析方法,用于研究两个变量之间的关系。它假设有一个自变量(输入变量)和一个因变量(输出变量)之间存在线性关系。简单线性回归的目标是建立一条直线,描述自变量和因变量之间的关系,使得通过该直线可以预测或解释因变量的值。
2.1.1 数学知识
简单线性回归模型的数学表示为: y = β 0 + β 1 x + ε y = \beta_0 + \beta_1x + \varepsilon y=β0+β1x+ε
其中, y y y是因变量, x x x是自变量, β 0 \beta_0 β0和 β 1 \beta_1 β1是回归方程的截距和斜率, ε \varepsilon ε是误差项,代表模型无法解释的随机误差。
在简单线性回归中,通过收集一组包含自变量和因变量值的数据,使用统计方法拟合直线,以找到最适合数据的回归线。这条拟合的直线可以帮助理解自变量和因变量之间的关系,并用于预测新的因变量值,基于给定的自变量值。简单线性回归是回归分析中的基础,它可以用于探索和量化两个变量之间的线性关系,但需要注意,它仅适用于具有线性关系的数据,并且在应用时需要满足一些假设前提。
2.1.2 应用举例
在python中来构建线性回归的模型非常多,比如scikit-learn,Statsmodels,TensorFlow,PyTorch,XGBoost,LightGBM,CatBoost等等,非常之多。在这里我们以 Python 中的 scikit-learn 库展示相应的代码。
假设我们有一组包含广告费用和销售额的数据,以此来建立简单的线性回归分析模型,代码如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成模拟数据
np.random.seed(1)
ad_costs = np.random.rand(100, 1) * 50 # 广告费用(假设范围在0到50之间)
sales = 15 + 0.5 * ad_costs + np.random.randn(100, 1) * 5 # 生成销售额数据(加入随机噪声)
# 绘制数据散点图
plt.scatter(ad_costs, sales, label='原始数据')
plt.title('广告费用与销售额关系')
plt.xlabel('广告费用')
plt.ylabel('销售额')
# 使用线性回归模型拟合数据
model = LinearRegression()
model.fit(ad_costs, sales)
# 打印R方,系数和截距
r_squared = model.score(ad_costs, sales)
print('R方值:', r_squared)
print('模型系数 (斜率):', model.coef_[0][0])
print('模型截距:', model.intercept_[0])
# 绘制回归线
plt.plot(ad_costs, model.predict(ad_costs), color='red', label='回归线')
plt.legend()
plt.show()
运行上述代码后,结果如下图:
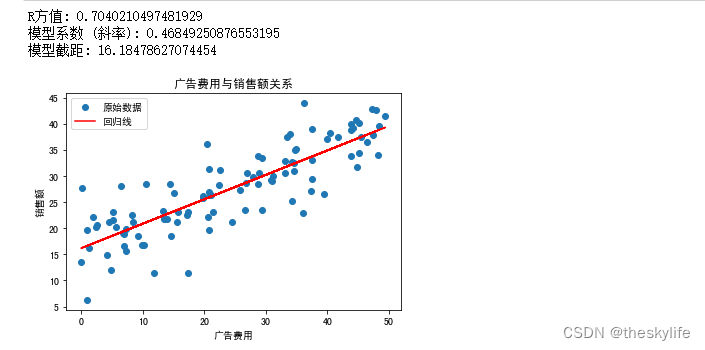
从上面的运行结果来看,建立的数据模型的R方值为0.704,这说明上述的线性回归模型,能解释70.4%的销售额变化。这个构建好的关系表达式为 y = 0.4685 ∗ x + 16.1848 y = 0.4685 * x +16.1848 y=0.4685∗x+16.1848。从R方的值来看,这个构建的模型效果还算ok,如果我们追求更高的拟合程度,可以考虑引入更多的特征、构建多项式回归、进行特征工程或使用其他模型。
2.2 多元线性回归
多元线性回归是用于研究多个自变量与一个因变量之间的关系。与简单线性回归不同,多元线性回归包含多个自变量,通过建立一个线性模型来探索和解释这些自变量与因变量之间的关系。
2.2.1 数学公式和应用
多元线性回归模型的数学表示为:
y = β 0 + β 1 x 1 + β 2 x 2 + … + β p x p + ε y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \ldots + \beta_px_p + \varepsilon y=β0+β1x1+β2x2+…+βpxp+ε
其中, y y y是因变量, x 1 , x 2 , … , x p x_1, x_2, \ldots, x_p x1,x
![速达软件全系产品任意文件上传漏洞复现 [附POC]](https://img-blog.csdnimg.cn/direct/2cd7921a38714229b3874330d47020a8.png)