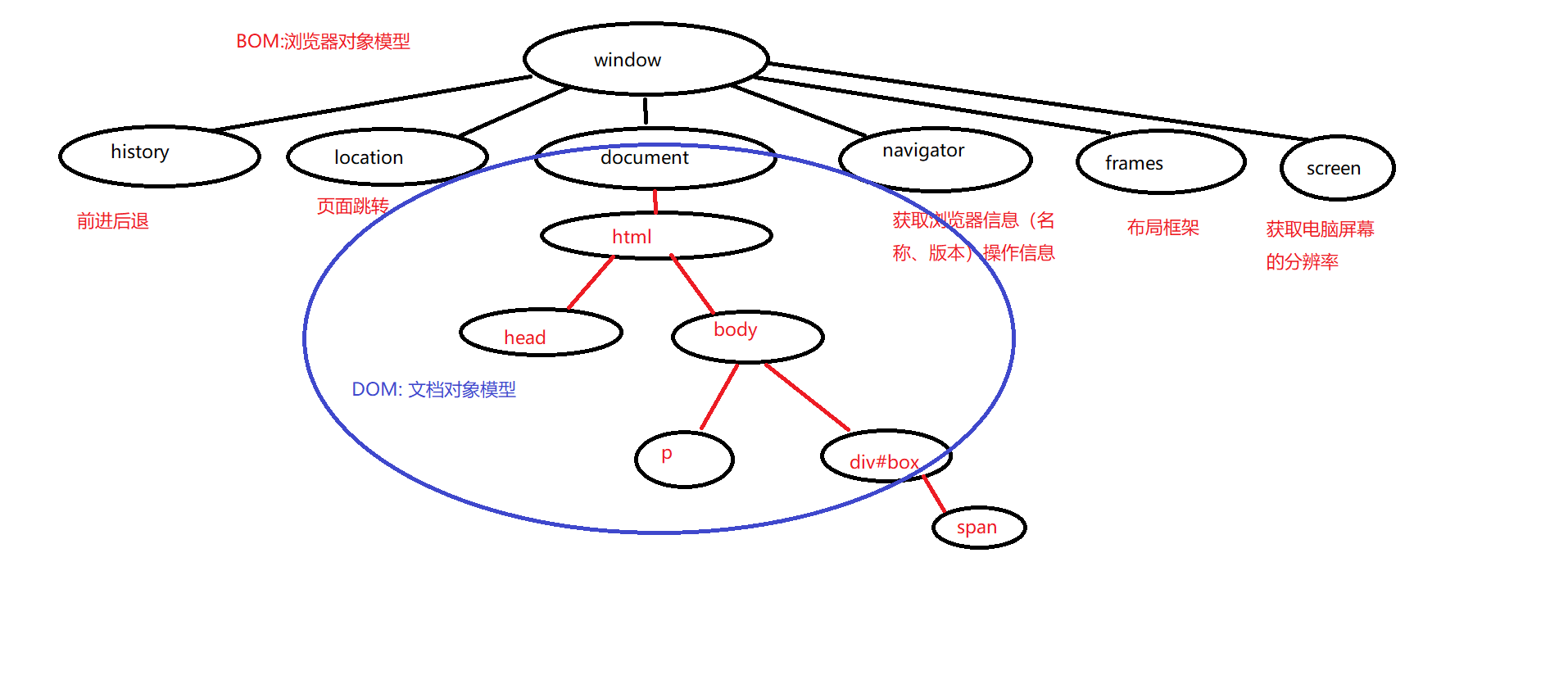
多重背包

有$N$件物品和一个容量是$M$的背包。第 $i$种物品最多有$s_i$件，每件的体积是$v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行两个整数，$N$，$M$，用空格隔开，分别表示物品数量和背包容积。

接下来有 $N$ 行，每行三个整数 $v_i$,$w_i$,$s_i$，用空格隔开，分别表示第 $i$ 件物品的体积，价值和数量。

输出格式

输出一个整数，表示最大价值。

样例 #1

样例输入 #1

4 5
1 2 3
2 4 1
3 4 3
4 5 2

样例输出 #1

10

提示

$0<N\le 1000,0<M\le 2000$

$0<v_i,w_i,s_i\le 2000$

算法思想

状态表示

多重背包的特点是第 $i$种物品最多有$s_i$件。仍可以采用01背包的思想，将处理每种物品作为一个阶段，考虑在不同背包容量情况下的最大价值，将其状态定义为$f[i][j]$，表示对于前$i$种物品，在背包容量为$j$的情况下，背包获得的最大价值。

状态计算

在当前阶段，对于第$i$种物品来说，有多种情况可以选择：

• 放入$0$件，此时的最大价值为前$i-1$种物品，在背包容量为$j$的情况下的最大价值$f[i-1][j]$。
• 放入$1$件，此时背包的最大价值为前$i-1$种物品，在背包容量为$j-v_i$的情况下的最大价值$f[i-1][j-v_i]+w_i$
• 放入$2$件，此时背包的最大价值为前$i-1$种物品，在背包容量为$j-2\times v_i$的情况下的最大价值$f[i-1][j-2\times v_i]+2\times w_i$
• …
• 放入$k$件，此时背包的最大价值为前$i-1$种物品，在背包容量为$j-k\times v_i$的情况下的最大价值$f[i-1][j-k\times v_i]+k\times w_i$
• …
• 放入$s_i$件，此时背包的最大价值为前$i-1$种物品，在背包容量为$j-s_i\times v_i$的情况下的最大价值$f[i-1][j-s_i\times v_i]+k\times w_i$

以上情况的前提是背包能够装得下$k$件第$i$种物品，也就是背包容量$j\ge k\times v_i$。那么，$f[i][j]$应该选择所有情况的最大值，即 f [ i ] [ j ] = max ⁡ { f [ i − 1 ] [ j − k × v i ] + k × w i } f[i][j] = \max\{f[i-1][j-k\times v_i]+k\times w_i\} f[i][j]=max{f[i−1][j−k×vi​]+k×wi​}，其中$0\le k\le s_i$，并且$k\times v_i\le j$。

初始状态

$f[0][0]$表示将前$0$种物品装入容量为$0$的背包中的产生的最大价值为$0$。

时间复杂度

• 状态数$n\times m$
• 状态计算时需要枚举第$i$件物品的数量$s_i$，时间复杂度为$O(s_i)$

总的时间复杂的为$O(n\times m\times s)$。

代码实现

#include <iostream>
using namespace std;
const int N = 1010, M = 2010;
int f[N][N];
int main(){
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        for(int j = 0; j <= m; j++)
        {
            for(int k = 0; k <= s && k * v <= j; k++)
            {
                f[i][j] = max(f[i][j], f[i - 1][j - k * v] + k * w);
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

算法优化

根据上述状态转移方程，考虑能否像完全背包一样的思路进行优化呢？

由 f [ i ] [ j ] = max ⁡ { f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − v ] + w , f [ i − 1 ] [ j − 2 × v ] + 2 × w + . . . + f [ i − 1 ] [ j − s × v ] + s × w } f[i][j] = \max\{f[i-1][j], f[i-1][j-v]+w, f[i-1][j-2\times v]+2\times w+...+f[i-1][j-s\times v]+s\times w\} f[i][j]=max{f[i−1][j],f[i−1][j−v]+w,f[i−1][j−2×v]+2×w+...+f[i−1][j−s×v]+s×w}

可得， f [ i ] [ j − v ] = max ⁡ { f [ i − 1 ] [ j − v ] , f [ i − 1 ] [ j − 2 × v ] + w , f [ i − 1 ] [ j − 3 × v ] + 2 × w + . . . + f [ i − 1 ] [ j − ( s + 1 ) × v ] + ( s + 1 ) × w } f[i][j - v] = \max\{f[i-1][j - v], f[i-1][j-2\times v]+w, f[i-1][j-3\times v]+2\times w+...+f[i-1][j-(s+1)\times v]+(s+1)\times w\} f[i][j−v]=max{f[i−1][j−v],f[i−1][j−2×v]+w,f[i−1][j−3×v]+2×w+...+f[i−1][j−(s+1)×v]+(s+1)×w}，

$f[i][j-v]$和$f[i][j]$和对比可以发现，多了一项$f[i-1][j-(s+1)\times v]+(s+1)\times w$。如果计算出$f[i][j-v]$，那么是否能得到$f[i][j]$呢？举个栗子：

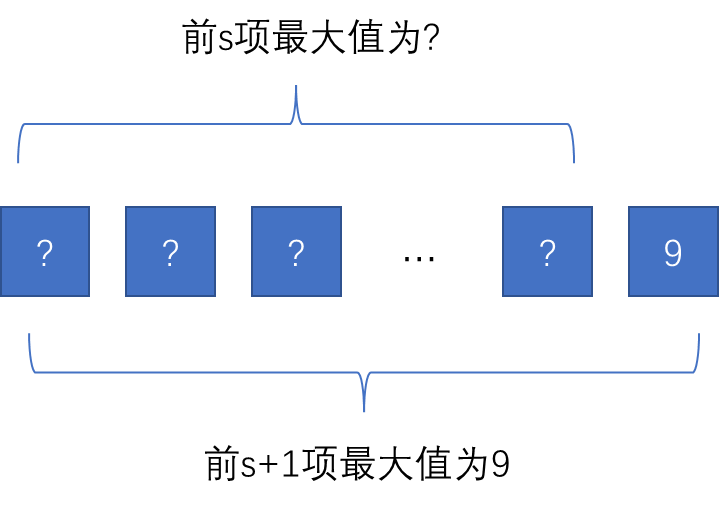
也就是说，知道前$s+1$项的最大值并不能计算出前$s$项的最大值，因此不能采用完全背包的思想来优化多重背包。

二进制枚举

在计算状态的过程中，需要枚举第$i$种物品的数量$[0,s_i]$，这里采用一种更高效的枚举方式——二进制枚举。例如当$s_i=1023$时，可以将第$i$种物品“打包”为：

• $0$件一组
• $1$件一组
• $2$件一组
• $4$件一组
• …
• $512$件一组

通过上述组与组之间的组合，可以表示出$[0,1023]$之间的任意一个数。如果把每组物品看成是01背包中的一种物品（仅能选择一次），那么就相当于用$10$个新物品来表示原来的第$i$个物品，通过组合这$10$个新物品就可以枚举出第$i$个物品的全部方案。

时间复杂度

• 状态数$n\times m$
• 通过上述思想，原来要枚举$s$次，现在只需要枚举$logs$次

总的时间复杂的为$(n\times m\times logs)$

代码实现

#include <iostream>
using namespace std;
const int N = 1010 * 12, M = 2010;
int v[N], w[N];
int f[M];
int main()
{
    int n, m, k = 0;
    cin >> n >> m;
    for(int i = 1; i <= n; i ++)
    {
        int a, b, s;
        cin >> a >> b >> s;
        //二进制拆分
        for(int j = 1; j <= s; j *= 2)
        {
            v[++ k] = j * a;
            w[k] = j * b;
            s -= j;
        }
        //拆分后还有剩余
        if(s) v[++ k] = s * a, w[k] = s * b;
    }
    n = k; //拆分后实际的物品数量
    //01背包
    for(int i = 1; i <= n; i ++)
        for(int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m];
    return 0;
}