已知数据集D中有9个数据点,分别是(1,2),(2,3),(2,1), (3,1),(2,4),(3,5),(4,3),(1,5),(4,2)。要求:
(1)采用层次聚类的聚集算法进行聚类,k=2。
(2)距离计算采用欧几里得距离。
(3)簇之间的距离采用单链接方式度量。
AGNES(Agglomerative Nesting)算法是一种层次聚类算法,它属于聚类分析中的一种。该算法通过不断地将最相似的数据点或聚类合并在一起,从而构建一个层次结构的聚类。这个过程是自下而上的,即从单个数据点或小的聚类开始,逐步合并形成更大的聚类,直到所有的数据点都被合并成一个大的聚类
步骤 1:初始化:将每个数据点视为一个单独的聚类。
步骤 2:计算距离矩阵:计算每一对数据点之间的欧几里得距离。
步骤 3:找到最小距离:找到距离矩阵中最小的距离,合并对应的两个数据点(或聚类)。
步骤 4:更新距离矩阵:根据合并的聚类更新距离矩阵。
步骤 5:重复步骤 3 和 4:重复上述步骤,直到得到k个聚类。
初始簇{1}, {2}, {3}, {4}, {5}, {6}, {7}, {8}, {9} 每个数据之间的欧几里得距离:
(1)采用层次聚类的聚集算法进行聚类,k=2。
(2)距离计算采用欧几里得距离。
(3)簇之间的距离采用单链接方式度量。
AGNES(Agglomerative Nesting)算法是一种层次聚类算法,它属于聚类分析中的一种。该算法通过不断地将最相似的数据点或聚类合并在一起,从而构建一个层次结构的聚类。这个过程是自下而上的,即从单个数据点或小的聚类开始,逐步合并形成更大的聚类,直到所有的数据点都被合并成一个大的聚类
步骤 1:初始化:将每个数据点视为一个单独的聚类。
步骤 2:计算距离矩阵:计算每一对数据点之间的欧几里得距离。
步骤 3:找到最小距离:找到距离矩阵中最小的距离,合并对应的两个数据点(或聚类)。
步骤 4:更新距离矩阵:根据合并的聚类更新距离矩阵。
步骤 5:重复步骤 3 和 4:重复上述步骤,直到得到k个聚类。
初始簇{1}, {2}, {3}, {4}, {5}, {6}, {7}, {8}, {9} 每个数据之间的欧几里得距离:
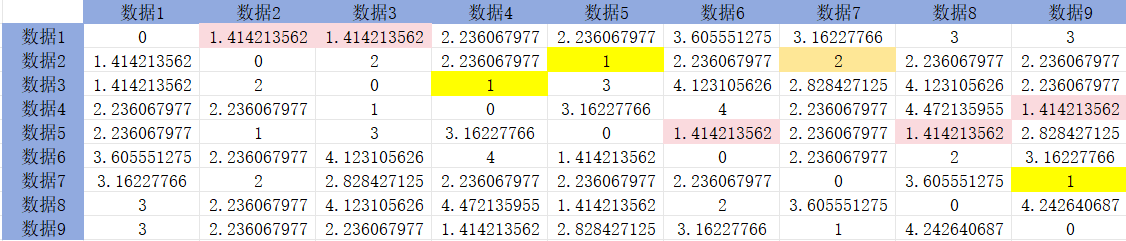
答案不唯一:
| 步骤 | 最近的簇距离 | 最近的两个簇 | 合并后的新簇 |
|---|---|---|---|
| 1 | 1 | {3},{4} | {3,4},{1}, {2}, {5}, {6}, {7}, {8}, {9} |
| 2 | 1 | {2},{5} | {3,4},{2,5}, {1}, {6}, {7}, {8}, {9} |
| 3 | 1 | {7}, {9} | {3,4},{2,5},{7,9}, {1}, {6}, {8} |
| 4 | 1.414 | {1},{3,4} | {1,3,4},{2,5},{7,9}, {6}, {8} |
| 5 | 1.414 | {6},{2,5} | {1,3,4},{2,5,6}, {7,9},{8}, |
| 6 | 1.414 | {8},{2,5,6} | {1,3,4},{2,5,6,8}, {7,9}, |
| 7 | 1.414 | {7,9},{1,3,4} | {1,3,4,7,9},{2,5,6,8}结束 |